Вы когда-нибудь задумывались о том, каким образом математика может описывать и предсказывать явления в нашем мире? Одной из самых важных и удивительных математических функций являются синус и косинус. Эти функции, несмотря на свою простоту, имеют огромное значение в различных областях науки и техники.
Синус и косинус, хоть и связаны неразрывно друг с другом, имеют свои отдельные значения и особенности. Каждый из них представляет собой математическую функцию, которая описывает отношение между сторонами прямоугольного треугольника. Возможно, вам уже удалось заметить ранее, что синус и косинус часто встречаются в физических или геометрических задачах.
Синус - это функция, которая позволяет нам вычислить соотношение между длиной противоположной стороны и гипотенузой прямоугольного треугольника. Она часто используется в геометрии для нахождения площадей и длин отрезков. Синус также имеет свои применения в физике, оптике, электронике и других областях науки.
Особенности функций в 90-градусном углу

Одной из основных черт, характерных для синуса в 90-градусном углу, является его максимальное значение, равное единице. Оно достигается, когда направление вектора в точке находится перпендикулярно оси X. Косинус же в этом углу обращается в ноль, что говорит о том, что вектор направлен параллельно оси Y.
Важно отметить, что данные значения функций встречаются не только при работе с геометрическими проблемами, но и в многих других областях науки и техники. Например, графическое представление зависимости электрического сигнала в электрических цепях от времени часто имеет форму синусоиды, где особенное значение получает синус 90 градусов. Аналогично, при расчете фазовых сдвигов в электронике, косинусу принадлежит роль ключевого компонента.
Продолжая изучать данные значения функций в 90-градусном углу, можно увидеть их аналогию в различных науках и областях. Например, в математике, особые значения функций используются для упрощения и решения различных уравнений и задач. В физике, синус и косинус 90 градусов играют важную роль при анализе циклических процессов и колебаний. Также, в компьютерной графике, знание данных значений помогает в реализации различных эффектов и визуализации объектов.
Способ вычисления синуса при угле 90 градусов
В данном разделе рассмотрим особенности вычисления синуса при угле, равном 90 градусам. Этот угол особенно интересен, так как он принимает максимальное значение для синуса.
Для вычисления синуса угла 90 градусов существует простая формула. Используя геометрическое понятие о синусе, который равен противоположной стороне к гипотенузе прямоугольного треугольника, мы можем установить, что для угла, равного 90 градусам, синус будет равен 1. Это означает, что длина противоположной стороны в таком треугольнике будет равна длине гипотенузы.
Подводя итог, формула для вычисления синуса угла 90 градусов может быть записана следующим образом:
- Синус(90°) = 1
Знание этой формулы важно в различных областях, где требуется работать с углами и синусами. Например, она может применяться в астрономии для расчета положения небесных объектов, а также в физике при моделировании движения тел. Понимание значения синуса 90 градусов позволяет удобно и точно решать задачи, связанные с углами и треугольниками.
Использование угла в 90° в тригонометрии
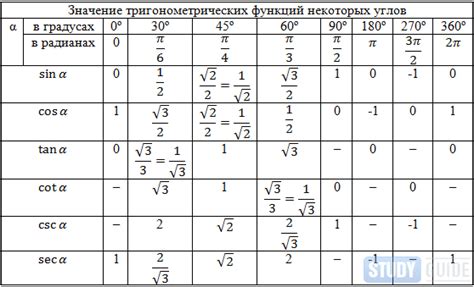
При рассмотрении угла в 90° в тригонометрии, особое внимание уделяется его синусу и косинусу. Синус 90° равен 1, а косинус 90° равен 0. Используя эти значения, можно решать уравнения, моделировать физические явления и строить сложные графики.
В технических и инженерных расчетах, синус и косинус 90° используются для определения фазовых сдвигов в электрических схемах, расчетов времени течения процессов, а также для точного позиционирования в пространстве при использовании глонасс и gps.
В геометрии, синус и косинус 90° помогают определить прямоугольные треугольники, вычислить площади и длины сторон этих треугольников, а также решить задачи на перпендикулярность и параллельность прямых.
В музыке, синусоиды, обусловленные значением синуса 90°, формируют основу многих инструментов, электронных звуков и звуковых эффектов. Использование синусоидальных колебаний позволяет создавать различные тональности и ритмические фигуры.
Таким образом, понимание и использование синуса 90° в тригонометрии является важной частью математического анализа и находит применение в различных областях, от технических расчетов до музыкальной композиции.
Формула для расчета значения косинуса при 90 градусах
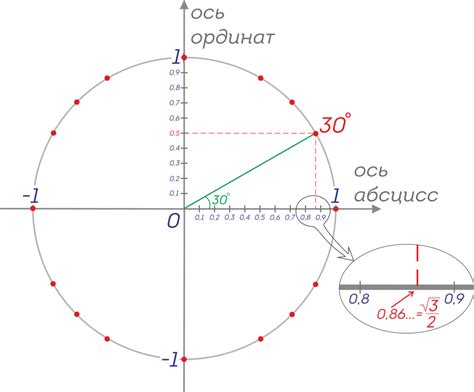
В данном разделе мы рассмотрим формулу, позволяющую вычислить значение косинуса для угла величины 90 градусов. С помощью этой формулы мы сможем получить точное значение косинуса и использовать его в различных математических и физических задачах.
Формула для вычисления косинуса угла 90 градусов представляет собой специальное выражение, которое придает этому углу уникальные свойства. В контексте геометрических фигур и треугольников, значение косинуса 90 градусов будет равно нулю. Это можно интерпретировать как то, что при прямом угле, катеты этого угла перпендикулярны друг другу, и косинус этого угла не даёт никакой дополнительной информации о форме или размере треугольника.
Применение косинуса 90 градусов в геометрии
| Применение | Описание |
|---|---|
| Нахождение длины катета | Косинус 90 градусов позволяет вычислить длину катета прямоугольного треугольника, зная значение гипотенузы и другого катета. Это особенно полезно при решении задач по нахождению длины сторон в геометрии. |
| Определение угла | Косинус 90 градусов также помогает определить угол между двумя сторонами треугольника. Путем вычисления отношения длины катета к гипотенузе можно найти величину этого угла, что позволяет строить и анализировать геометрические фигуры. |
| Построение прямых и углов | Зная значение косинуса 90 градусов, можно строить прямые и углы с заданными характеристиками. Это особенно актуально при работе с техническими чертежами и дизайном, где точность и правильность построений играют важную роль. |
Таким образом, косинус 90 градусов имеет широкий спектр применения в геометрии, обеспечивая точные вычисления и позволяя строить геометрические объекты с заданными характеристиками.
Соотношение между синусом и косинусом при угле 90 градусов

В данном разделе мы рассмотрим взаимосвязь между значениями синуса и косинуса при угле, равным 90 градусов. Рассмотрим эту связь с точки зрения геометрии и алгебры.
Геометрический подход позволяет наглядно представить соотношение между синусом и косинусом при угле 90 градусов. Когда угол равен 90 градусов, его синус равен 1, а косинус равен 0. Это означает, что при таком угле точка на единичной окружности, представляющей значения синуса и косинуса, находится на верхней границе окружности. В этой точке синус достигает своего максимального значения, а косинус становится равным нулю.
Алгебраический подход позволяет выразить соотношение между синусом и косинусом при угле 90 градусов в виде математической формулы. Если обозначить синус угла α как sin(α) и косинус угла α как cos(α), то при α = 90 градусов синус равен 1, а косинус равен 0, что записывается как sin(90°) = 1 и cos(90°) = 0.
| Угол (градусы) | Синус | Косинус |
|---|---|---|
| 90° | 1 | 0 |
Связь между синусом и косинусом при угле 90 градусов имеет важное практическое применение в различных областях, таких как физика, инженерия, астрономия и другие. Это позволяет решать задачи, связанные с расчетами на основе синусов и косинусов углов, в частности при решении треугольников и моделировании движения.
Практическое применение синуса и косинуса 90 градусов в задачах
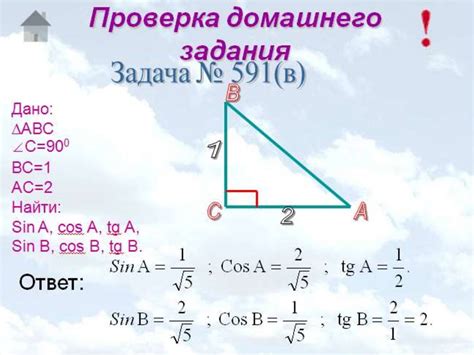
Используя свойства синуса и косинуса при угле 90 градусов, можно решать различные задачи, связанные с геометрией, физикой и инженерией.
1. Решение треугольников:
С помощью синуса и косинуса 90 градусов можно определить длины сторон треугольника и измерения его углов. Это полезно для построения искомого треугольника, а также для нахождения его площади, высоты и других характеристик.
2. Расчет физических параметров:
Синус и косинус 90 градусов применяются для определения направлений сил, скоростей, ускорений и других физических величин. Например, при моделировании движения тела в пространстве необходимо знать углы и направления, чтобы точно определить траекторию и скорость.
3. Разработка инженерных систем:
В инженерии синус и косинус 90 градусов используются для проектирования и анализа различных систем. Например, при проектировании мостов или зданий важно учитывать углы наклона, чтобы обеспечить необходимую прочность и устойчивость конструкции.
4. Навигация и геодезия:
С использованием синуса и косинуса 90 градусов можно определять направление и расстояние между объектами на карте или в реальном мире. Это полезно для навигации, геодезических измерений и ориентации в пространстве.
Важно понимать, что значение синуса и косинуса 90 градусов всегда равно 1 и 0 соответственно. Благодаря этому свойству, эти тригонометрические функции находят широкое практическое применение в различных задачах и науках.
Вопрос-ответ

Какие значения имеют синус и косинус 90 градусов?
Значение синуса 90 градусов равно 1, а значение косинуса 90 градусов равно 0.
Как можно выразить значения синуса и косинуса 90 градусов в виде формулы?
Формула для синуса 90 градусов: sin(90°) = 1. Формула для косинуса 90 градусов: cos(90°) = 0.
Почему значение синуса 90 градусов равно 1, а косинуса равно 0?
Значение синуса 90 градусов равно 1, потому что синус является противоположным катетом, который равен гипотенузе в прямоугольном треугольнике с углом 90 градусов. Значение косинуса 90 градусов равно 0, потому что косинус является прилежащим катетом, который равен нулю в прямоугольном треугольнике с углом 90 градусов.
Какие применения имеют значения синуса и косинуса 90 градусов в математике и физике?
В математике и физике значения синуса и косинуса 90 градусов используются для нахождения trigonometric identity и решения уравнений, связанных с геометрическими и треугольными конструкциями. Они также играют важную роль при решении задач, связанных с колебаниями, волнами и периодическими функциями.



