Уверены, что знаете все существующие способы решения геометрических задач? Большинство из нас учило в школе традиционные методы нахождения вписанной дуги и применения их в различных ситуациях. Однако, мир геометрии огромен и полон удивительных открытий. Что, если мы расскажем вам о новых и нестандартных способах, которыми можно решить задачу?
В данной статье мы рассмотрим инновационные подходы, которые позволяют найти вписанную дугу, не прибегая к стандартным методам. Забудьте о том, что вы знаете, и окунитесь в мир открытий и неожиданностей! Вы обнаружите, что геометрия может быть не только трудной и скучной, но и захватывающей и захватывающей!
Смело открывайте новые горизонты геометрии вместе с нашей командой экспертов! Мы предлагаем вам не просто набор формул и алгоритмов, а настоящие задачи и головоломки, которые потребуют от вас креативного мышления и умения подойти к проблеме с необычной стороны.
Теорема о соотношении вписанных углов и дуг в окружности
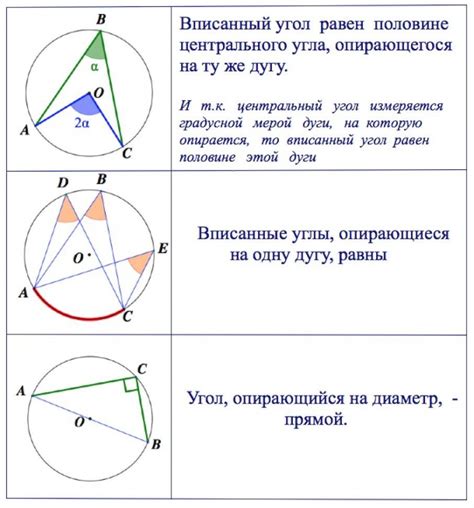
В геометрии существует важная теорема, связывающая углы и дуги вписанные в окружность. Эта теорема позволяет определить связь между углами, образованными вписанными хордами, и дугами, охватываемыми ими на окружности.
Важно понимать, что в окружности угол и дуга, охватываемая этим углом, являются соответствующими частями одного и того же объекта - окружности. Поэтому изменение угла автоматически приводит к изменению охватываемой им дуги и наоборот. Это своего рода взаимосвязь, которая специфична для окружности и дает нам возможность решать различные геометрические задачи.
Теорема о вписанных углах и дугах гласит, что угол, образованный двумя пересекающимися в одной точке хордами, равен половине суммы мер дуг, охватываемых этими хордами. То есть мы можем выразить эту зависимость через равенство мер угла и полусуммы мер двух дуг на окружности. Это равенство позволяет нам решать задачи, связанные с вписанными углами и дугами.
Теорема о вписанных углах и дугах имеет широкое применение в геометрии, позволяя решать задачи на построение, вычисление длин дуг и другие задачи, связанные с окружностями. Понимание этой теоремы позволяет анализировать и видеть связи между углами и дугами, что является важным аспектом геометрии и использования окружностей в практических задачах.
Геометрическое понятие влезающей огибающей
Концепция влезающей огибающей широко используется в различных задачах, связанных с определением геометрических параметров фигур. Её применение позволяет не только определить различные характеристики фигуры, но и решить практические задачи, связанные с проектированием, строительством и другими отраслями.
В основе определения влезающей огибающей лежит концепция касательных, занимающихся внутри заданной фигуры. Каждый касательный точно задевает фигуру и идет по кратчайшему пути между двумя точками касания. Исходя из этой идеи, влезающая огибающая может быть определена как кривая, которая является множеством всех касательных, занимающихся внутри фигуры.
Определение влезающей огибающей имеет широкий спектр применений, начиная от геометрических задач, таких как определение площади или периметра фигуры, и заканчивая практическими задачами, такими как построение мостов, определение оптимальных путей и многое другое. Знание и понимание этого геометрического понятия позволяет решать разнообразные задачи эффективно и точно.
- Определение влезающей огибающей.
- Применение в геометрических задачах.
- Значимость влезающей огибающей в практических задачах.
Расчет длины дуги, вписанной в геометрическую фигуру

В данном разделе будут рассмотрены методы и алгоритмы для определения длины дуги, которая лежит внутри геометрической фигуры и касается ее на двух точках.
Нахождение длины такой дуги является важной задачей в геометрии и находит применение в различных областях, например, в физике, строительстве и дизайне.
В процессе рассмотрения будут использованы различные методы и формулы, позволяющие точно определить длину вписанной дуги.
Одним из таких методов является использование геометрической формулы для нахождения длины дуги, которая основывается на радиусе окружности и угле, опирающемся на эту дугу. Полученное значение можно использовать для решения конкретных задач и применения в практике.
Задачи на определение радиуса окружности при наличии вписанной дуги
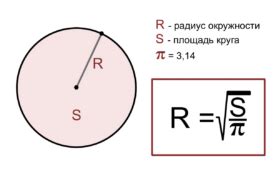
В данном разделе рассмотрим интересные задачи, связанные с определением радиуса окружности, когда известна информация о вписанной дуге. Решение данных задач позволит нам более глубоко понять взаимосвязь между радиусом окружности и вписанной дугой, а также продемонстрирует практическое применение этих знаний в геометрии.
Мы рассмотрим несколько типов задач, в каждой из которых будет использоваться вписанная дуга. Например, задача о найденном треугольнике с известным радиусом окружности и длиной вписанной дуги позволит нам определить значения углов этого треугольника. Или задача о построении квадрата, вписанного в окружность, на основе известной вписанной дуги позволит нам определить длину стороны квадрата и радиус окружности.
Для решения этих задач нам понадобятся определенные формулы и существующие связи между радиусом и длиной дуги. Благодаря этому мы сможем найти неизвестные величины и решить поставленные задачи.
| Тип задачи | Общие данные | Искомая величина |
|---|---|---|
| Задача 1: Треугольник с заданной вписанной дугой | Радиус окружности, длина вписанной дуги | Значения углов треугольника |
| Задача 2: Квадрат, вписанный в окружность | Радиус окружности, длина вписанной дуги | Длина стороны квадрата, радиус окружности |
| Задача 3: Построение вписанного пятиугольника | Радиус окружности, длина вписанной дуги | Длина сторон пятиугольника |
Решение данных задач поможет нам почувствовать практическую пользу от знаний о вписанных дугах в геометрии и дать представление о применении этих знаний в реальной жизни. Ответы на поставленные задачи помогут нам лучше понять свойства окружностей и их взаимосвязь с геометрическими фигурами.
Применение кривой, описанной внутри фигуры, при вычислении площади

В данном разделе рассмотрим использование специальной кривой, находящейся внутри геометрической фигуры, при расчете ее площади. Эта кривая, известная как вписанная дуга, позволяет нам получить более точные и удобные формулы для определения площади различных фигур.
Для начала рассмотрим применение вписанной дуги при вычислении площади круга. Вписанная дуга является частью окружности посередине круга и образует определенный угол. Зная радиус круга и длину этой дуги, мы можем использовать соответствующую формулу для вычисления площади круга. Такой подход позволяет точнее определить площадь круга, особенно при использовании более сложных формул, включающих тригонометрические функции.
Теперь обратимся к другим геометрическим фигурам, таким как треугольники и многоугольники. Вписанная дуга может быть использована для разделения этих фигур на более простые составляющие, которые могут быть более легко измерены и вычислены. Например, при разделении треугольника вписанной дугой на два сегмента, мы можем применить формулы для площади треугольника к каждому из сегментов отдельно, а затем сложить полученные результаты. Такой подход может быть полезен при работе с треугольниками, имеющими сложные формы или над которыми проведены сложные конструкции.
| Преимущества применения вписанной дуги при вычислении площади | Примеры применения |
|---|---|
| - Более точные результаты | - Вычисление площади круга с использованием вписанной дуги |
| - Упрощение сложных вычислений | - Разделение треугольника вписанной дугой для более удобного расчета площади |
| - Применение к различным геометрическим фигурам | - Расчет площади многоугольников с использованием вписанной дуги |
Определение центра окружности по заданной вписанной кривой
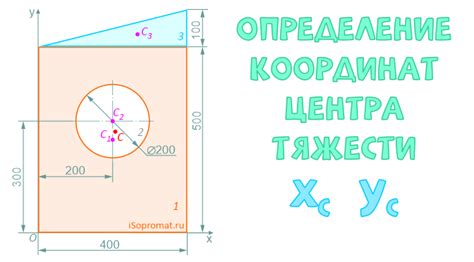
Этот раздел посвящен решению задач, связанных с нахождением центра окружности при заданной вписанной дуге. Подобно многим другим задачам геометрии, решение таких задач требует применения различных методов и инструментов. Благодаря этому, можно найти точное положение центра окружности и решить задачу с высокой точностью.
В работе с задачами этого типа, важно понимать, что вписанная дуга является дугой окружности, которой касается внутренний угол. Чтобы найти центр окружности по данной геометрической фигуре, необходимо использовать различные геометрические приемы и методы, такие как построение перпендикуляров, а также использование свойств треугольников и касательных.
Каждая задача на нахождение центра окружности по вписанной дуге имеет свои особенности и требует индивидуального подхода. В данном разделе будут представлены несколько примеров задач с подробным описанием алгоритма решения и использованных геометрических принципов. Кроме того, будет рассмотрена их практическая применимость и использование в реальных ситуациях.
| Пример задачи | Алгоритм решения | Практическое применение |
|---|---|---|
| Задача 1 | Описание алгоритма решения задачи 1 | Пример практического применения решения задачи 1 |
| Задача 2 | Описание алгоритма решения задачи 2 | Пример практического применения решения задачи 2 |
| Задача 3 | Описание алгоритма решения задачи 3 | Пример практического применения решения задачи 3 |
Вопрос-ответ

Для чего нужно находить вписанную дугу в геометрии?
Нахождение вписанной дуги в геометрии может помочь в решении различных задач, таких как вычисление площади фигуры с помощью радиуса вписанной окружности, определение углов между хордами и дугами, а также построение прямых и касательных линий к окружности. Это важный инструмент для анализа и изучения геометрических фигур.
Как найти вписанную дугу в геометрии?
Для нахождения вписанной дуги в геометрии нужно знать радиус вписанной окружности и центр этой окружности. Если известен радиус окружности и угловая мера дуги, можно вычислить длину дуги с помощью формулы L = r * α, где L - длина дуги, r - радиус окружности, α - угловая мера дуги в радианах.
Какие задачи можно решить с помощью вписанной дуги в геометрии?
С помощью вписанной дуги в геометрии можно решить задачи вычисления площади фигуры, определения углов между хордами и дугами, построения прямых и касательных линий к окружности. Например, можно использовать вписанную дугу для вычисления площади сектора или сегмента окружности, определения угла пересечения двух хорд или построения касательной линии к окружности в заданной точке.
Как использовать вписанную дугу для вычисления площади фигуры?
Для вычисления площади фигуры с помощью вписанной дуги нужно знать радиус вписанной окружности и угловую меру дуги, ограничивающей эту фигуру. Сначала нужно найти длину дуги с помощью формулы L = r * α, где L - длина дуги, r - радиус окружности, α - угловая мера дуги в радианах. Затем можно применить формулу для вычисления площади сектора окружности: S = 0.5 * r^2 * α.
Какие способы существуют для нахождения вписанной дуги в геометрии?
Для нахождения вписанной дуги в геометрии существуют несколько способов. Один из них - построение окружности, вписанной в данную фигуру. Для этого нужно провести перпендикуляр из центра окружности к одной из сторон фигуры и построить радиус. Еще один способ - использование угла, вписанного в дугу. Если известен угол, то его можно использовать для нахождения радиуса окружности и длины дуги.
Какие задачи можно решить с помощью вписанной дуги в геометрии?
С помощью вписанной дуги в геометрии можно решать разные задачи. Например, можно определить площадь фигуры, ограниченной вписанной дугой и сторонами фигуры. Для этого нужно знать радиус окружности и угол, вписанный в дугу. Также можно находить центр окружности, вписанной в фигуру, с помощью вписанной дуги. Для этого нужно определить три точки на дуге и провести перпендикуляры из середин сторон фигуры к этим точкам. Это поможет найти центр окружности.