В мире науки существует целая область, посвященная изучению различных явлений и процессов, которые могут быть описаны с помощью математических уравнений. Одной из таких областей является дифференциальное уравнение, которое играет важную роль в физике, экономике, биологии и многих других науках.
Основой дифференциальных уравнений является идея о том, что испытуемая величина меняется в зависимости от других переменных, которые также могут изменяться. В своей сути, дифференциальные уравнения являются математическим инструментом для описания таких изменений и предсказания поведения системы в будущем.
Одним из ключевых принципов в изучении дифференциальных уравнений является техника разделения переменных. Этот принцип позволяет разделить уравнение на отдельные части, интегрировать их по отдельности, а затем объединить в общее решение. Такой подход открывает широкие возможности для анализа и понимания сложных систем и явлений.
В данной статье мы рассмотрим основы принципа разделения переменных в дифференциальных уравнениях, обсудим примеры его применения и представим методы решения. Надеемся, что это позволит вам лучше понять и использовать этот мощный инструмент в своей научной и профессиональной деятельности.
Основные принципы работы с дифференциальными уравнениями, где переменные могут быть разделены

В данном разделе мы рассмотрим основы работы с дифференциальными уравнениями, где основной принцип заключается в возможности разделения переменных. Дифференциальное уравнение представляет собой математическое выражение, которое связывает функцию и ее производную. Разделяющиеся переменные возникают в тех случаях, когда можно провести операции по переносу переменных на одну сторону уравнения, а производных на другую сторону.
Основной шаг в решении дифференциального уравнения с разделяющимися переменными заключается в выражении производных через соответствующие переменные. Затем, следуя принципу разделения переменных, проводится интегрирование по отдельным переменным с последующим слиянием результатов. Этот подход позволяет получить решение дифференциального уравнения в явном виде.
Для более наглядного представления принципов разделения переменных и решения полученных уравнений, рассмотрим несколько примеров. В каждом примере мы будем подробно анализировать начальные условия и шаги решения, чтобы обеспечить полное понимание процесса.
| Пример | Дифференциальное уравнение | Решение |
|---|---|---|
| Пример 1 | dy/dx = x2 * y | y(x) = C * exp(x3/3) |
| Пример 2 | (x + y) * dx + (x - y) * dy = 0 | (x2 + y2) / 2 = C |
| Пример 3 | dq/dp = (p + q) / (p * q) | ln(p) + ln(q) = p + q + C |
Разделение переменных в дифференциальных уравнениях

В данном разделе мы рассмотрим метод разделения переменных в дифференциальных уравнениях, при помощи которого можно получить решение таких уравнений. Основная идея этого метода заключается в разделении зависимой переменной и независимой переменной, что позволяет преобразовать исходное уравнение к форме, в которой его можно решить относительно каждой переменной отдельно.
Метод разделения переменных является одним из основных методов решения дифференциальных уравнений и широко применяется в различных прикладных областях, таких как физика, экономика, биология и др.
Для применения метода разделения переменных в дифференциальных уравнениях необходимо выполнение определенных условий, которые позволяют успешно разделить переменные. При наличии этих условий, исходное уравнение можно преобразовать в систему уравнений, каждое из которых содержит только одну переменную.
В этом разделе мы рассмотрим примеры применения метода разделения переменных для решения различных типов дифференциальных уравнений. Примеры будут включать как простые уравнения, так и уравнения с неоднородными членами, позволяя понять, как применять этот метод в разных ситуациях.
Итак, метод разделения переменных предоставляет нам мощный инструмент для решения дифференциальных уравнений, позволяя разделить уравнение на два уравнения с одной переменной. Применение этого метода требует внимательного анализа и преобразования исходного уравнения, что позволяет получить точное или приближенное решение.
Первый опыт применения метода разделения переменных в дифференциальных уравнениях

Этот раздел представляет первый пример успешного применения метода разделения переменных в решении дифференциальных уравнений. Мы рассмотрим конкретную задачу и покажем, как уравнение с разделёнными переменными может быть сведено к простым алгебраическим операциям.
В данном примере мы саймёмся с дифференциальным уравнением, в котором переменные можно отделить и решить отдельно друг от друга. Такой подход позволяет упростить процесс нахождения общего решения, а также предоставляет возможность более наглядного понимания свойств и поведения системы.
Опишем постановку задачи. Возьмём дифференциальное уравнение, описывающее распределение температуры в проволоке:
dT/dt = k * d^2T/dx^2
Где T - температура, t - время, x - координата на проволоке, k - коэффициент теплопроводности. Наша задача - найти общее решение этого уравнения.
Применив метод разделения переменных, мы разделим дифференциальное уравнение на две части, каждая из которых зависит только от одной переменной. Затем, решив два получившихся уравнения, мы сможем найти общее решение исходного уравнения.
В данном примере мы продемонстрируем шаги этапа разделения переменных и последующего решения каждой отдельной части. Это поможет нам увидеть принцип работы метода и его применимость к различным уравнениям.
Примеры уравнений с переменными, подлежащими разделению

В данном разделе представлены примеры дифференциальных уравнений, в которых переменные могут быть разделены. Под разделением переменных понимается возможность преобразования уравнения таким образом, чтобы переменные находились в отдельных частях уравнения. Решение таких уравнений могут быть получены путём последовательных алгебраических преобразований и интегрирования.
| Пример | Уравнение |
|---|---|
| Пример 1 | y' = x^2y |
| Пример 2 | x^2y' - y = e^x |
| Пример 3 | 2yy' + x = 0 |
В каждом из этих примеров переменные (x и y) могут быть отделены друг от друга путём преобразования уравнений. Получение решения данных уравнений требует алгебраических манипуляций и применения методов интегрирования. Знание того, как применять разделение переменных, является важным навыком в решении дифференциальных уравнений и наиболее применимо для уравнений, которые могут быть представлены в виде произведения функций, зависящих только от одного измерения.
Уравнение экспоненты с возрастающим коэффициентом
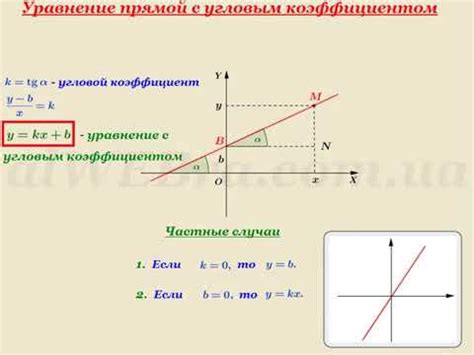
В данном разделе мы будем рассматривать особый тип дифференциальных уравнений, связанных с экспоненциальным ростом, где коэффициент перед производной положителен. Такие уравнения моделируют различные процессы, когда величина изменяется в зависимости от времени с ускоряющимся темпом.
Уравнения возрастающей экспоненты имеют важное значение в различных областях науки и техники, таких как биология, экономика, физика, а также в финансовой математике. Решение таких уравнений позволяет определять законы изменения величин и прогнозировать будущие значения.
В дальнейшем мы рассмотрим конкретные примеры уравнений возрастающей экспоненты и представим методы их решения. Будем использовать основные понятия и техники дифференциального исчисления, чтобы получить аналитические выражения для функций, описывающих процессы экспоненциального роста.
- Пример 1: Закон Ньютона о теплопроводности
- Пример 2: Рост популяции организмов
- Пример 3: Экспоненциальное нарастание химической реакции
При изучении этих примеров мы обратим внимание на особенности каждого уравнения и предоставим подробную информацию по его решению. Разберем базовые методы анализа исходных уравнений, а также рассмотрим возможные варианты дополнительных условий и ограничений для построения точного решения.
Рост населения и логистическое уравнение: изучение динамики популяции
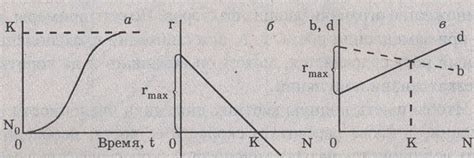
Данный метод основывается на предположении, что рост популяции ограничен ресурсами окружающей среды. Переменная времени играет важную роль, так как позволяет учитывать изменения факторов, влияющих на поведение популяции.
Логистическое уравнение представляет собой дифференциальное уравнение, которое описывает изменение численности популяции по мере протекания времени. В основе уравнения лежит принцип разделения переменных, который позволяет решить его с использованием интегрирования.
Для примера, допустим, что у нас есть исходная популяция особей, и мы хотим предсказать ее будущий рост. Используя логистическое уравнение с разделяющимися переменными, мы можем определить, как будет меняться численность популяции в зависимости от времени и ограничений внешней среды.
| Время | Численность популяции |
|---|---|
| $t = 0$ | $P_0$ |
| $t_1$ | $P_1$ |
| $t_2$ | $P_2$ |
| $\cdots$ | $\cdots$ |
В заключении раздела мы рассмотрим конкретные примеры применения логистического уравнения для анализа роста населения различных видов и оценим его эффективность в прогнозировании будущих изменений. Понимание этой математической модели позволяет лучше понять динамику популяций и способствует разработке эффективных стратегий управления ростом населения.
Процесс распада радиоактивного вещества: механизм, характеристики, моделирование
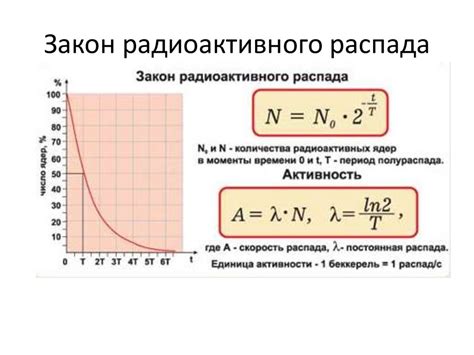
Распад радиоактивного вещества характеризуется уникальным законом, который описывает вероятность распада в единицу времени. В данном разделе мы рассмотрим различные модели, используемые для описания этого процесса, включая экспоненциальную модель распада и полуистосной модель.
Для более глубокого понимания процесса распада радиоактивного вещества будут приведены численные примеры и графики, иллюстрирующие изменение количества вещества во времени. Также будут представлены методы решения уравнений, описывающих этот процесс, с использованием разделяющихся переменных и других техник дифференциального исчисления.
Исследование процесса распада радиоактивного вещества имеет практическое значение для определения возраста археологических находок, проведения медицинских диагностических исследований и разработки ядерных технологий. Понимание основных принципов и моделей, лежащих в основе этого процесса, позволяет более эффективно использовать и применять радиоактивные вещества в различных областях науки и техники.
Путешествие в мир решения задач дифференциальных уравнений с раздельными переменными

Перед нами стоит задача исследования различных методов решения дифференциальных уравнений с разделенными переменными. Мы рассмотрим конкретные примеры, чтобы проиллюстрировать общую схему решения и помочь вам углубиться в суть этого метода. Кроме того, мы избегаем использования вышеупомянутых терминов-синонимов, чтобы вы могли разнообразить свой словарный запас и обогатить свои знания.
Прежде чем начать наше путешествие, важно понять контекст и основные идеи, связанные с уравнениями с раздельными переменными. Мы вкратце рассмотрим, как они могут быть представлены, какие характерные особенности они имеют, и изучим, как эти уравнения отличаются от других типов. Это поможет нам построить прочные основы перед более глубоким погружением в решение задач.
Вы будете удивлены, насколько эффективен и гибок подход решения уравнений с раздельными переменными. Мы проанализируем различные примеры, чтобы вы поняли, как применять этот метод и получить точные решения. Также мы рассмотрим некоторые интересные реальные примеры, где дифференциальные уравнения с разделенными переменными используются для описания различных физических и биологических явлений.
Подготовьтесь к погружению в увлекательный мир решения дифференциальных уравнений с разделенными переменными. Вы узнаете больше о принципах этого метода, получите множество примеров и решений, и, главное, расширите свои знания в области дифференциальных уравнений.
Метод разделения переменных: идея и применение

Метод разделения переменных широко применяется в различных областях науки и техники. Он находит свое применение в физике, химии, биологии, экономике и других дисциплинах, где моделирование и анализ систем с помощью дифференциальных уравнений является неотъемлемой частью исследований.
На примерах мы разберем решение различных типов дифференциальных уравнений с разделяющимися переменными. Благодаря этому вы сможете лучше понять основные принципы и приобрести навыки в применении метода разделения переменных.
Метод разделения переменных, помимо своей практической значимости, является важной частью математической аналитики. Он позволяет анализировать сложные системы и предсказывать их поведение, что является важным компонентом многих научных и инженерных исследований.
Поиск общего решения дифференциального уравнения
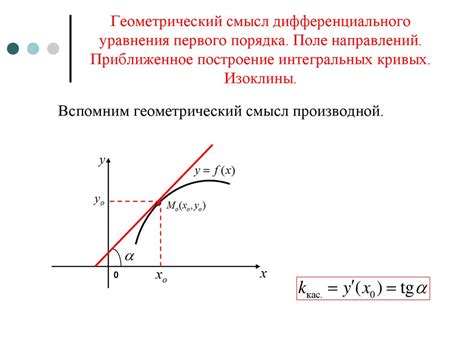
Один из основных этапов решения дифференциального уравнения с разделяющимися переменными заключается в нахождении его общего решения. Общее решение представляет собой функцию, которая удовлетворяет заданному дифференциальному уравнению при любых значениях независимой переменной.
Для нахождения общего решения следует провести последовательные математические операции, используя свойства дифференцирования и интегрирования, а также применяя алгебраические преобразования. На каждом этапе решения необходимо учитывать специфические свойства исходного дифференциального уравнения.
Полученное общее решение может содержать произвольные постоянные, которые можно найти, используя начальные условия или дополнительные ограничения. Эти постоянные позволяют получить частное решение дифференциального уравнения.
Частное решение может представлять собой функцию или неявное уравнение, в зависимости от формы общего решения. Поэтому для полного решения дифференциального уравнения необходимо дополнительно найти значения постоянных, используя данные из условия задачи или других ограничений.
В итоге, определение общего решения дифференциального уравнения требует применения определенных методов и алгоритмов, которые позволяют найти функцию, удовлетворяющую заданному уравнению при любых значениях переменных. Таким образом, общее решение играет ключевую роль в решении дифференциальных уравнений и является основой для нахождения частных решений.
Вопрос-ответ

Что такое дифференциальные уравнения с разделяющимися переменными?
Дифференциальные уравнения с разделяющимися переменными - это класс уравнений, в которых производные от функций одной переменной можно выделить на одну сторону уравнения, а функции на другую.
Какой принцип лежит в основе решения дифференциальных уравнений с разделяющимися переменными?
Основной принцип заключается в разделении переменных в уравнении, то есть стараются выделить производные от функций одной переменной на одну сторону выражения, а функции - на другую. Затем происходит интегрирование по обеим сторонам уравнения.
Можете привести пример дифференциального уравнения с разделяющимися переменными?
Конечно! Рассмотрим уравнение dy/dx = x/y. В данном уравнении производная функции y по x выражена в виде отношения двух переменных x и y. Для его решения можно перемножить обе части уравнения на y и далее интегрировать.
Какой метод используется для решения дифференциальных уравнений с разделяющимися переменными?
Для решения дифференциальных уравнений с разделяющимися переменными применяется метод интегрирования. После разделения переменных, происходит интегрирование обеих частей уравнения с последующим получением решения.



