Алгоритмическое моделирование - это увлекательный процесс создания интеллектуальных систем, способных делать предсказания и прогнозы на основе имеющихся данных. Важной частью этого процесса является линейная регрессия, в которой само имя говорит нам о преобладании простоты и прямолинейности в принятии решений.
Как строительница основных контуров моделей машинного обучения, линейная регрессия стремится найти самую простую и наиболее понятную связь между переменными при помощи формулы. Ее главная цель - предсказать значения зависимой переменной на основе наблюдаемых значений одной или нескольких независимых переменных.
Уникальность линейной регрессии заключается в том, что она базируется на представлении экспериментальных данных в виде прямой линии на графике. Это создает возможность прогнозировать значения целевой переменной в диапазоне значений независимой переменной. С помощью этой простой модели мы можем получить понимание взаимосвязи между двумя или более переменными и использовать эту информацию для прогнозирования будущих событий и результатов.
Определение и основные принципы моделирования зависимостей с помощью линейной регрессии
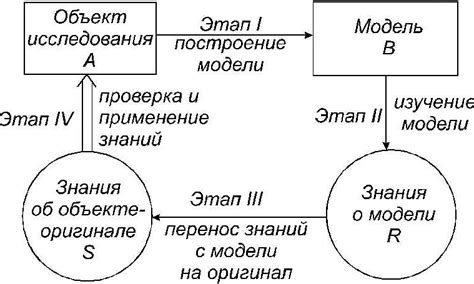
Основной принцип линейной регрессии заключается в поиске и определении линейной связи между зависимой переменной (целевой переменной) и одной или более независимых переменных (предикторов). Линейная регрессия строит линию (или гиперплоскость в общем случае), которая наилучшим образом соответствует данным и позволяет сделать прогнозы или провести анализ.
В основе линейной регрессии лежит предположение о линейной зависимости между переменными, что означает, что изменение одной переменной пропорционально изменению другой переменной с постоянным коэффициентом. При построении модели линейной регрессии используется метод наименьших квадратов, который минимизирует сумму квадратов отклонений предсказанных значений от фактических.
Самое интересное в линейной регрессии заключается в анализе коэффициентов модели. Эти коэффициенты указывают на величину и направление влияния каждой независимой переменной на зависимую переменную. Кроме того, можно обнаружить статистическую значимость этих влияний с помощью стандартных ошибок и p-значений. Такой анализ позволяет понять, какие переменные особенно важны и как они взаимодействуют друг с другом.
Определение и принцип работы модели линейной регрессии
Идея линейной регрессии заключается в том, чтобы получить линейное уравнение, которое наилучшим образом соответствует наблюдаемым данным. Линейная регрессия строит линию или гиперплоскость в многомерном пространстве, аппроксимирующую зависимость между переменными. Такая линия или гиперплоскость позволяет предсказывать значения зависимой переменной на основе заданных значений независимых переменных.
Процесс построения модели линейной регрессии начинается с обучающего набора данных, где каждая запись представляет собой пару значений независимых переменных и соответствующее значение зависимой переменной. Путем нахождения оптимальных параметров, таких как коэффициенты наклона и свободного члена, модель определяет наилучшую гиперплоскость, минимизируя разницу между предсказанными значениями и фактическими значениями зависимой переменной.
- Если рассматриваемая задача имеет только одну независимую переменную, то говорят о простой линейной регрессии.
- В случае, когда в модели присутствуют две или более независимых переменных, используется множественная линейная регрессия.
Линейная регрессия широко применяется в различных областях, таких как экономика, физика, социология и обработка данных. Важно отметить, что она представляет лишь один из инструментов машинного обучения и может давать хорошие результаты только в пределах своих ограничений. Для более сложных задач, возможно, потребуется использование более продвинутых моделей.
Математическое описание модели

Суть линейной регрессии заключается в поиске оптимальной прямой линии, которая наилучшим образом аппроксимирует данные и обладает наименьшими отклонениями от них. Для этого используется метод наименьших квадратов, который позволяет найти такие значения параметров модели, при которых сумма квадратов разностей между реальными значениями и значениями, предсказанными моделью, будет минимальной. Таким образом, модель линейной регрессии стремится найти оптимальное математическое описание исследуемой системы.
В математическом виде модель линейной регрессии представляется уравнением вида:
y = a + bx
где y - зависимая переменная, a - свободный член, b - коэффициент наклона прямой, x - независимая переменная. Таким образом, модель линейной регрессии представляет собой уравнение прямой линии, которая наилучшим образом описывает взаимосвязь между независимыми и зависимой переменными.
Оценка параметров модели производится с помощью метода наименьших квадратов, который минимизирует сумму квадратов разностей между фактическими значениями зависимой переменной и значениями, предсказанными моделью. Для этого используются различные алгоритмические методы, позволяющие найти оптимальные значения параметров модели.
Как строится математическая модель в методе линейной регрессии
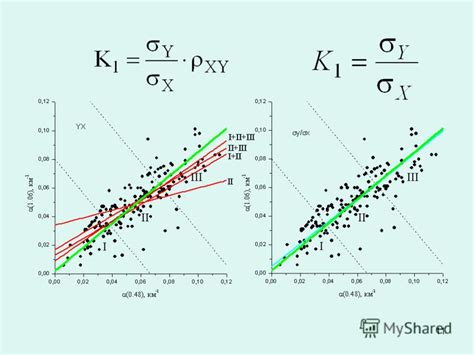
Для построения математической модели в методе линейной регрессии используются определенные принципы и алгоритмы, которые позволяют анализировать и предсказывать взаимосвязи между переменными. Основная идея этого подхода заключается в нахождении оптимального вектора весов, который минимизирует ошибку предсказания и обеспечивает наилучшую аппроксимацию данных.
Первоначально необходимо провести предварительный анализ данных, что включает в себя их сбор, обработку и преобразование. Затем необходимо выбрать подходящую функцию, которая будет аппроксимировать данные. В линейной регрессии обычно используются аффинные функции, такие как линейная или полиномиальная функции с постоянными коэффициентами.
Следующим шагом является выбор оптимальных параметров модели, то есть вектора весов, которые будут учитывать влияние каждой переменной на предсказываемую величину. В линейной регрессии эти веса находятся путем минимизации функции ошибки, например, суммы квадратов разностей между предсказанными и фактическими значениями. Для этого применяются различные методы оптимизации, такие как метод наименьших квадратов или градиентный спуск.
После нахождения оптимальных параметров модели, ее можно использовать для предсказания значений зависимой переменной на основе новых данных. При этом следует учитывать, что модель является статистической аппроксимацией и предсказания могут быть неточными. Поэтому для оценки точности и надежности модели проводятся дополнительные статистические тесты и анализ ошибок предсказания.
- Предварительный анализ данных.
- Выбор подходящей функции для аппроксимации данных.
- Выбор оптимальных параметров модели.
- Предсказание значений зависимой переменной.
- Оценка точности и надежности модели.
Обучение модели линейной зависимости
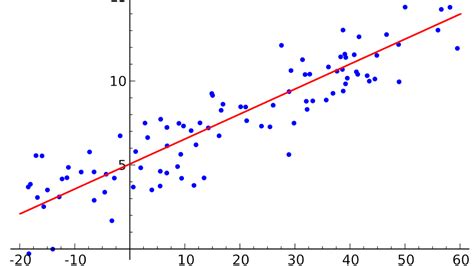
В данном разделе мы рассмотрим процесс обучения модели, способной находить линейную зависимость между данными.
При обучении модели линейной зависимости мы стремимся найти такую прямую линию, которая наилучшим образом описывает наши данные. Данная линия будет приближать и предсказывать значения зависимой переменной на основе независимых переменных.
Обучение модели линейной зависимости основано на методе наименьших квадратов, которая позволяет оценить параметры прямой линии, минимизируя сумму квадратов отклонений предсказанных значений от фактических данных. При этом, каждый параметр регрессии имеет свой вес, определяющий вклад в предсказание зависимой переменной.
Процесс обучения модели линейной зависимости включает выбор или создание соответствующего набора данных, подготовку этих данных (например, удаление выбросов или заполнение пропущенных значений), разделение данных на тренировочные и тестовые наборы, а также применение алгоритма обучения к тренировочным данным для определения оптимальных параметров модели.
В результате обучения модели линейной зависимости, мы получаем уравнение прямой линии, которое можно использовать для предсказания значений зависимой переменной на основе новых или неизвестных данных.
Процесс настройки и подбора параметров модели
Изучение
Перед тем, как начать обучение модели, необходимо тщательно изучить доступные данные и установить связи между ними. Важно понять, какие признаки (факторы) оказывают влияние на целевую переменную, чтобы определить, какие коэффициенты модели следует регулировать. Это могут быть сильные физические законы или просто эмпирические зависимости между данными.
Составление математической модели
На основе полученных данных и предварительного анализа составляется математическая модель линейной регрессии. В этой модели коэффициенты представляют собой параметры, значения которых подбираются в процессе обучения. Отбор значимых признаков и учет различных взаимодействий между ними являются важным этапом для достижения наилучшего качества предсказания.
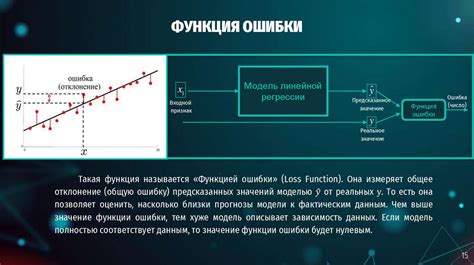
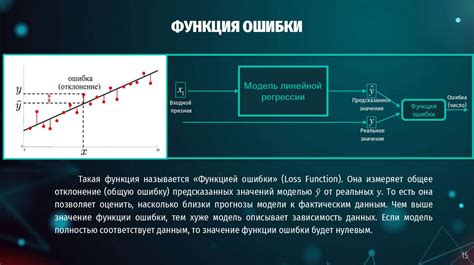
Функция потерь и оптимизация
Для выбора наиболее подходящих значений коэффициентов модели используется функция потерь, которая измеряет разницу между предсказанными и фактическими значениями. Цель состоит в том, чтобы минимизировать эту разницу и достичь наилучшей соответствия предсказаниям на тренировочных данных. Для оптимизации функции потерь применяются различные алгоритмы, такие как градиентный спуск, которые автоматически обновляют значения параметров с целью уменьшения ошибки.
Подгонка и кросс-валидация
После итеративного процесса обучения и предварительной настройки модели, она должна быть подогнана на полном наборе данных для получения окончательных значений коэффициентов. При этом важно проверить качество предсказания на новых, неизвестных ранее данных. Для этого применяется кросс-валидация, которая позволяет оценить стабильность и надежность модели.
Таким образом, процесс обучения и выбора коэффициентов модели линейной регрессии основан на тщательной настройке параметров и оптимизации функции потерь с помощью алгоритмов и методов машинного обучения. Это позволяет создать модель, способную предсказывать значения целевой переменной на основе входных данных с высокой точностью и достоверностью.
Примеры применения линейной регрессии в реальной жизни
Одной из областей, в которой линейная регрессия успешно применяется, является финансовый анализ. Например, финансовые аналитики применяют линейную регрессию для прогнозирования цен на акции и другие финансовые инструменты. Они используют исторические данные, такие как цены акций в прошлом, объем торгов и другие факторы, чтобы предсказать будущие изменения цен.
Линейная регрессия также широко используется в маркетинге и рекламе. Маркетологи могут использовать этот алгоритм для анализа данных о продажах и рекламных кампаниях, чтобы выявить влияние различных факторов на объем продаж. Например, они могут изучать, как объем продаж зависит от бюджета на рекламу, количества показов рекламы и других факторов. Это позволяет оптимизировать маркетинговые стратегии и увеличить эффективность кампаний.
Кроме того, линейная регрессия применяется в медицине для прогнозирования заболеваний и оценки эффективности лекарственных препаратов. Медицинские исследователи могут использовать этот алгоритм для анализа данных о пациентах, таких как возраст, рост, вес, семейная история болезни и другие факторы, чтобы определить риск развития определенного заболевания. Это позволяет раннее выявлять пациентов с высоким риском и предпринимать профилактические меры.
В заключении, линейная регрессия является мощным инструментом прогнозирования, который широко применяется в реальной жизни. Она позволяет нам находить зависимости между переменными и использовать их для прогнозирования значений. Примеры применения линейной регрессии включают финансовый анализ, маркетинг и рекламу, а также медицину. Этот алгоритм имеет большой потенциал в различных областях и продолжает развиваться для решения новых задач.
Применение линейной регрессии в различных сферах
В экономике линейная регрессия используется для прогнозирования роста экономических показателей, оценки влияния различных факторов на доходы, анализа рыночных трендов и выявления причинно-следственных связей.
В маркетинге данная методика применяется для определения влияния рекламных кампаний на продажи, анализа поведения потребителей, определения оптимальной цены продукта и прогнозирования спроса.
В медицине линейная регрессия используется для прогнозирования развития заболеваний, оценки эффективности лекарственных препаратов, анализа влияния факторов окружающей среды на здоровье и построения прогностических моделей в рамках общественного здравоохранения.
Линейная регрессия находит свое применение также в геологии для прогнозирования эффективности добычи полезных ископаемых, в сфере финансов для прогнозирования курсов валют и оценки рисков, в социологии для анализа социальных процессов и многих других областях, где требуется анализ и прогнозирование данных.
Вопрос-ответ

Как работает линейная регрессия?
Линейная регрессия - это метод машинного обучения, который позволяет предсказывать зависимую переменную на основе одной или нескольких независимых переменных. Основная идея состоит в том, чтобы создать линейную функцию, которая наилучшим образом соответствует имеющимся данным. Для этого используется обучающая выборка, на основе которой находятся коэффициенты линейной функции. Коэффициенты определяют величину и направление влияния каждой независимой переменной на зависимую переменную. В результате получается уравнение, которое позволяет предсказывать значения зависимой переменной для новых наблюдений.
Какие преимущества имеет линейная регрессия?
Линейная регрессия является простым и интерпретируемым методом. Он не требует большого количества данных и вычислительных ресурсов для обучения модели. Кроме того, линейная регрессия позволяет провести анализ влияния каждой независимой переменной на зависимую переменную. Это может быть полезно при решении задачи прогнозирования или выявлении факторов, влияющих на исследуемый процесс или явление.
Как выбрать подходящую функцию для линейной регрессии?
Выбор подходящей функции для линейной регрессии зависит от характера данных и целей исследования. В общем случае, можно использовать линейную функцию вида y = b0 + b1*x, где y - зависимая переменная, x - независимая переменная, b0 и b1 - коэффициенты модели. Однако, в некоторых случаях может потребоваться добавление в модель полиномиальных или других функций для лучшего описания зависимости между переменными. Выбор функции требует анализа данных и экспертных знаний о предметной области исследования.



