Одним из ключевых аспектов логической оптимизации является преобразование формул в Сокращенную Дизъюнктивную Нормальную Форму (СДНФ) и Конъюнктивную Нормальную Форму (КНФ).
Данный процесс потребуется при анализе и упрощении логических выражений. Преобразование формул в СДНФ и КНФ позволяет эффективно проводить различные операции с выражениями, а также упрощать их структуру.
В данной статье будут рассмотрены различные методы и подходы к преобразованию формул в СДНФ и КНФ, а также предоставлены инструкции, которые помогут вам освоить эффективные стратегии оптимизации логических выражений.
Оппоненты могут утверждать, что данный процесс является сложным и трудоемким. Однако, с помощью правильного выбора методов и инструкций, вы сможете значительно повысить свою эффективность и достичь оптимального результата.
Методы улучшения логических функций в сетях с полной ДНФ
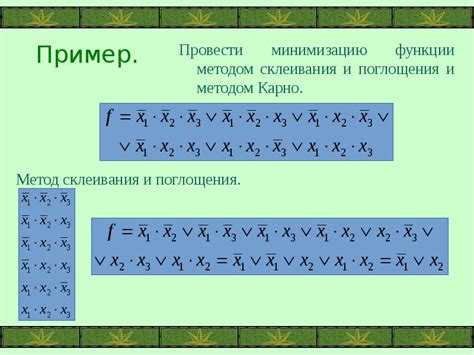
В этом разделе мы рассмотрим различные подходы и техники, которые могут быть использованы для оптимизации логических функций в сетях, где используется полная дизъюнктивная нормальная форма (ПДНФ). ПДНФ представляет функцию в виде суммы произведений литералов, где каждое произведение представляет одно из возможных наборов входных переменных, при которых функция принимает значение 1.
Оптимизация логических функций играет важную роль в построении эффективных схем, так как позволяет сократить количество логических элементов, затрачиваемых на реализацию функции. В данном разделе мы рассмотрим несколько основных методов оптимизации функций в ПДНФ:
- Метод поглощения: данный метод позволяет упростить выражение функции, удаляя из него лишние произведения, которые не влияют на ее результат.
- Метод максимального склеивания: основная идея этого метода заключается в нахождении максимально возможного числа произведений, которые могут быть объединены в одно.
- Метод компактного представления: данный метод позволяет представить функцию в сокращенной форме, используя сокращенные наборы литералов.
- Методы использования специальных логических элементов: некоторые логические элементы, такие как импликаторы или исключающее ИЛИ (XOR) могут быть использованы для упрощения выражения функции.
Каждый из этих методов имеет свои особенности и преимущества, поэтому их выбор зависит от конкретной задачи оптимизации и требований к сети. Подробнее мы рассмотрим каждый метод и представим примеры его применения.
Основы приведения СДНФ к КНФ: ключевые концепции и принципы

Приведение СДНФ к КНФ позволяет существенно упростить выражение, сделать его более компактным и понятным, а также установить логические связи между переменными. В основе этого процесса лежит переход от дизъюнкций к конъюнкциям, используя логические операции И и НЕ.
Одним из ключевых понятий, используемых при преобразовании, является понятие литерала. Литерал представляет собой переменную или ее отрицание. Успешное преобразование требует сочетания литералов в определенных конъюнктивных формах, которые могут быть более эффективно обработаны.
Другим важным понятием является покрытие. Покрытие – это комбинация конъюнкций, которые образуют КНФ и полностью описывают все возможные варианты комбинаций значений переменных. Цель состоит в том, чтобы найти оптимальное покрытие, которое минимизирует количество конъюнкций, при этом полностью описывая все допустимые комбинации.
В ходе преобразования будет применяться ряд принципов, направленных на упрощение и оптимизацию КНФ. Один из таких принципов – исключение элементов, не затрагивающих функциональность системы. Также важно осознавать роль консенсуса и универсальных дизъюнкций при создании оптимальных КНФ.
В следующих разделах мы рассмотрим более подробно эти понятия и принципы, а также предоставим пошаговые инструкции по преобразованию СДНФ в КНФ с использованием различных методов и стратегий оптимизации.
Структура и синтаксис СДНФ: ключевые аспекты понимания
В этом разделе мы рассмотрим основные элементы и узнаем о структуре и синтаксисе СДНФ, одного из важнейших инструментов логической алгебры. Как мы знаем, СДНФ помогает представить функцию в виде суммы произведений литералов, где каждое произведение соответствует одному максимально-простому набору дизъюнкций.
Перед тем, как погрузиться в детали, проанализируем общую структуру СДНФ и ее основные составляющие элементы. Чтобы лучше понять этот вид представления функции, рассмотрим его на примере. Допустим, у нас есть функция, которая описывает работу умного дома. СДНФ поможет нам выразить логические условия, при которых работает определенное устройство, используя литералы, операции ИЛИ и И, а также скобки для группировки условий.
Важный аспект понимания СДНФ - это правила синтаксиса, которые определяют, каким образом нужно записывать функцию в виде суммы произведений. Здесь важна последовательность и использование соответствующих символов, таких как литералы переменных, знаки операций и скобки. Умение корректно применять правила синтаксиса СДНФ позволит нам правильно переводить функцию в другие формы представления и проводить дальнейшую оптимизацию логических выражений.
Процедура приведения формул логики к представлению, удобному для оптимизации

Процедура преобразования формул из стандартной дизъюнктивной нормальной формы (СДНФ) в конъюнктивную нормальную форму (КНФ) является одним из подходов к оптимизации логических функций. В данном разделе будет рассмотрена процедура приведения формул к представлению в КНФ, которое облегчает последующую оптимизацию и упрощение логического выражения.
Основная идея процедуры заключается в преобразовании формулы СДНФ в эквивалентную формулу КНФ с помощью логических операций и правил алгебры логики. В результате преобразования формула будет состоять из конъюнкций литералов, что упростит процесс анализа и оптимизации.
При преобразовании СДНФ в КНФ могут быть использованы различные методы и алгоритмы, включающие в себя дистрибутивные законы, перестановки и комбинирование конъюнкций и дизъюнкций. Данный раздел предоставит инструкции и рекомендации для эффективного применения этих методов, а также примеры и практические рекомендации по преобразованию СДНФ в КНФ с целью оптимизации логических функций.
| Плюсы процедуры преобразования СДНФ в КНФ: | Минусы процедуры преобразования СДНФ в КНФ: |
| Упрощение и оптимизация логических функций | Возможность увеличения количества конъюнкций и литералов |
| Удобство анализа и дальнейшей оптимизации | Затраты на временные ресурсы при выполнении процедуры преобразования |
Методы приведения булевых выражений в эквивалентные формы

Для эффективного анализа и оптимизации логических функций в информационных системах широко применяется метод приведения булевых выражений из СДНФ к КНФ. Данная статья предлагает подробные инструкции по использованию различных методов преобразования, позволяющих достичь максимальной эффективности в оптимизации логических схем.
В первую очередь рассматривается понятие булевых функций и их вариантов представления с использованием СДНФ и КНФ. Затем детально изучаются основные методы преобразования из СДНФ в КНФ, включая введение новых переменных, использование законов алгебры логики, использование принципа Де Моргана и т.д. Каждый метод описывается шаг за шагом, с приведением примеров и пояснений для лучшего понимания процесса.
Важным моментом является анализ сложности каждого преобразования и возможности выбора наиболее эффективных методов в зависимости от контекста использования. Приводятся сравнительные характеристики различных методов, а также примеры оптимизированных выражений, полученных в результате преобразования СДНФ в КНФ.
Особое внимание уделено применению преобразования СДНФ в КНФ в реальных проектах информационных систем. Описываются типичные задачи, в которых данный процесс может быть полезен, а также способы решения конкретных проблем, возникающих при оптимизации логических функций с использованием различных методов преобразования.
| Преимущества | Недостатки |
|---|---|
| Упрощение логических выражений | Не всегда возможно достичь минимального числа конъюнкций в КНФ |
| Улучшение производительности логических схем | Требует дополнительных вычислительных ресурсов для преобразования |
| Улучшение понимания и документирования логических выражений | Может быть сложно определить наиболее эффективные методы преобразования в конкретной ситуации |
Используя рекомендации и инструкции данной статьи, разработчики и аналитики смогут достичь оптимальных результатов при преобразовании булевых выражений из СДНФ в КНФ. Это позволит не только улучшить производительность информационных систем, но и повысить эффективность и надежность их работы.
Методы повышения эффективности при оптимизации логических функций

Для достижения лучших результатов при оптимизации логических функций, существует ряд методов, которые позволяют улучшить эффективность данного процесса. Они направлены на уменьшение сложности выражений в логическом виде, исключение излишних операторов и приближение к более компактному представлению функции.
Одним из методов является сокращение числа переменных в выражении функции. Это достигается путем замены группы переменных на их сумму или произведение. Также возможно применение различных алгоритмов и эвристик для определения комбинаций переменных, которые можно объединить.
Другой метод, позволяющий улучшить эффективность оптимизации логических функций, - это замена сложных операторов на более простые. Например, можно заменить оператор "или" на сумму или произведение, оператор "и" на произведение или сумму, а оператор "не" на отрицание или исключение.
Важным аспектом для сокращения сложности логических функций является анализ и устранение излишних термов и подвыражений. Это возможно путем удаления дубликатов, объединения и упрощения подвыражений, а также применения алгоритмов для поиска и удаления избыточных термов.
Также следует учитывать возможность применения различных эвристик для повышения эффективности оптимизации логических функций. Например, использование правил коммутативности и ассоциативности, а также определение порядка выполнения операций для минимизации сложности функции.
Применение КНФ для более эффективного вычисления логических функций
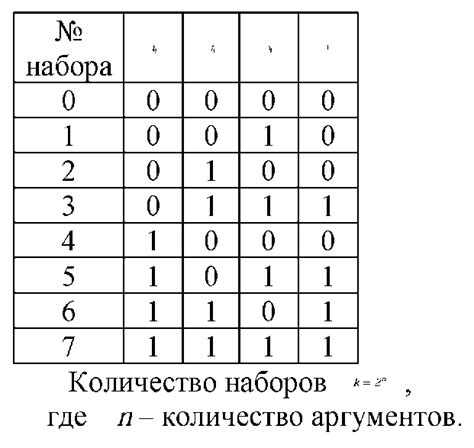
В данном разделе мы рассмотрим применение Конъюнктивной нормальной формы (КНФ) в контексте вычисления логических функций. КНФ представляет собой формулу, состоящую из конъюнкций литералов, и обладает свойством легкого вычисления значений функции, что может привести к повышению эффективности и оптимизации работы с логическими выражениями.
Применение КНФ позволяет сократить время вычисления логических функций, упростить логические выражения и обеспечить возможность использования более оптимизированных методов анализа и оптимизации кода. Благодаря использованию КНФ, можно представить сложные логические выражения более компактно и удобно для последующего анализа и обработки.
- Преимущества применения КНФ:
- Увеличение скорости выполнения логических операций;
- Снижение сложности логических выражений;
- Облегчение отладки и анализа кода;
- Повышение эффективности работы с логическими функциями.
Процесс использования КНФ включает в себя преобразование исходной логической функции в конъюнктивную нормальную форму, что позволяет представить функцию в виде конъюнкций литералов. Изменение формы представления функции может повысить её понятность и облегчить процесс её анализа, оптимизации и исполнения.
В итоге, применение КНФ позволяет использовать более эффективные методы обработки и оптимизации логических функций, ускоряет процесс вычисления и позволяет представить функцию в форме, удобной для дальнейшего анализа и оптимизации.
Примеры улучшения логических функций с использованием приведения дизъюнктивной нормальной формы (ДНФ) к конъюнктивной нормальной форме (КНФ)

В данном разделе представлены конкретные примеры иллюстрирующие процесс оптимизации логических функций с помощью преобразования ДНФ в КНФ. Метод анализа и преобразования логических выражений, основанный на выполнении СДНФ-КНФ преобразования, позволяет улучшить эффективность работы с логическими функциями и сократить сложность их вычисления.
Пример 1: Пусть имеется логическая функция с двумя входами A и B. Исходная функция представлена в СДНФ:
Ф = (A ∙ B) + (A ∙ B') + (A' ∙ B)
Процесс преобразования начинается с упрощения полученной ДНФ, путем исключения повторяющихся термов и использования алгебраических тождеств. В итоге получаем следующую упрощенную ДНФ:
Ф = (A ∙ B) + (A' ∙ B)
Затем производится преобразование упрощенной ДНФ в эквивалентную КНФ. Применяется закон дистрибутивности, путем раскрытия скобок и группировки одинаковых переменных:
Ф = (A ∙ B) + (A' ∙ B) = (A + A') ∙ (B + B)
Функция, представленная в КНФ после преобразования, имеет вид:
Ф = (A + A') ∙ (B + B) = 1
Таким образом, в результате преобразования СДНФ в КНФ, логическая функция была упрощена до постоянного значения, что обеспечивает более эффективное вычисление и оптимизацию.
Пример 2: Рассмотрим другой пример логической функции с тремя входами A, B и C:
Ф = (A ∙ B ∙ C) + (A' ∙ B ∙ C) + (A ∙ B' ∙ C) + (A ∙ B ∙ C')
Процесс преобразования СДНФ в КНФ начинается с упрощения исходной ДНФ:
Ф = (A ∙ B ∙ C) + (A' ∙ B ∙ C) + (A ∙ B' ∙ C) + (A ∙ B ∙ C')
Упрощенная ДНФ выглядит следующим образом:
Ф = (A ∙ B ∙ C) + (A' ∙ B ∙ C) + (A ∙ B' ∙ C) + (A ∙ B ∙ C')
Затем производится преобразование упрощенной ДНФ в эквивалентную КНФ:
Ф = (A ∙ B ∙ C) + (A' ∙ B ∙ C) + (A ∙ B' ∙ C) + (A ∙ B ∙ C')
После раскрытия скобок и группировки одинаковых переменных получаем КНФ следующего вида:
Ф = (A + A') ∙ (B + B) ∙ (C + C) = 1
В результате преобразования логической функции, она также была упрощена до постоянного значения, что позволяет сократить сложность вычислений и оптимизировать процесс работы с функцией.
Преимущества и ограничения практического применения метода преобразования СДНФ в КНФ

Преимущества метода преобразования СДНФ в КНФ
- Универсальность: метод применим к различным типам логических функций и выражений.
- Понятность и легкая интерпретация: КНФ дает возможность ясно понять логическую структуру выражения и ее основные свойства.
- Повышение эффективности: преобразование СДНФ в КНФ может помочь упростить выражение и привести его к более компактному виду.
- Удобство в использовании: после преобразования СДНФ в КНФ, с ним можно работать, используя такие операции, как сопряжение и дизъюнкция, что упрощает анализ и дальнейшие операции с логическим выражением.
Ограничения метода преобразования СДНФ в КНФ
- Рост количества переменных: при преобразовании СДНФ в КНФ происходит увеличение количества переменных, что может усложнить дальнейший анализ и обработку выражения.
- Потеря информации при упрощении: в процессе преобразования СДНФ в КНФ возможна потеря некоторых деталей и информации, что может привести к неправильному анализу или неполному решению задачи.
- Ограниченная применимость: метод может иметь ограничения в применении к сложным логическим функциям или выражениям, которые требуют более сложных методов оптимизации.
В целом, метод преобразования СДНФ в КНФ является полезным инструментом для оптимизации и анализа логических выражений. Однако, важно учитывать его преимущества и ограничения при его практическом использовании.
Важность преобразования СДНФ в КНФ в области вычислительной логики

СДНФ представляет собой логическую формулу, состоящую из элементарных дизъюнкций, где каждая дизъюнкция представляет одно из возможных сочетаний значений переменных. В то же время, КНФ представляет собой формулу, состоящую из элементарных конъюнкций, где каждая конъюнкция представляет одно из возможных сочетаний значений переменных.
Преобразование СДНФ в КНФ имеет значительные преимущества в области вычислительной логики. Упрощение логического выражения путем преобразования в КНФ позволяет достичь более компактного, эффективного и понятного представления логической функции, упрощает ее анализ и позволяет использовать другие методы и техники в дальнейшем исследовании и оптимизации.
Также важно отметить, что преобразование СДНФ в КНФ позволяет уменьшить количество элементов в выражении, что в свою очередь приводит к более эффективной обработке и расчетам на практике. Более компактное и оптимизированное представление функций часто оказывает наибольшее влияние на характеристики систем, основанных на вычислительной логике, позволяя улучшить производительность и снизить стоимость решений.
Таким образом, преобразование СДНФ в КНФ играет важную роль в области вычислительной логики, позволяя оптимизировать и анализировать логические функции, повышать их эффективность и применять различные методы и техники для достижения максимального оптимального результата.
Вопрос-ответ

Что такое СДНФ и КНФ?
СДНФ (сокращенно Совершенная Дизъюнктивная Нормальная Форма) и КНФ (сокращенно Конъюнктивная Нормальная Форма) являются двумя основными формами представления логических функций в вычислительной логике. СДНФ представляет функцию в виде дизъюнкции (логического ИЛИ) множества литералов (переменных или их отрицаний), которые образуют конъюнкции (логическое И) всех вариантов значений переменных, при которых функция истинна. КНФ, наоборот, представляет функцию в виде конъюнкции множества литералов, формирующих дизъюнкции всех возможных значений переменных, при которых функция ложна.
Зачем преобразовывать СДНФ в КНФ?
Преобразование СДНФ в КНФ может быть полезным для оптимизации и упрощения логических функций. КНФ имеет некоторые преимущества перед СДНФ, так как некоторые виды аппаратуры или программного обеспечения могут работать более эффективно с функциями, представленными в КНФ. Кроме того, преобразование может помочь улучшить понимание и анализ логических функций.
Какие методы могут быть использованы для преобразования СДНФ в КНФ?
Существует несколько методов для преобразования СДНФ в КНФ. Один из таких методов - это метод двойственности, который заключается в отрицании каждого литерала и замене операций ИЛИ на И, а И на ИЛИ. Еще один метод - это метод Квайна, который основан на применении законов логики для упрощения и преобразования выражений.
Какие инструкции можно использовать для эффективной оптимизации преобразования СДНФ в КНФ?
Для эффективной оптимизации преобразования СДНФ в КНФ можно использовать несколько инструкций. Во-первых, стоит упростить и минимизировать исходную СДНФ перед преобразованием, используя законы алгебры логики. Во-вторых, следует выбирать подходящий метод преобразования, учитывая сложность функции и требования к ее представлению. Наконец, стоит проверять полученную КНФ на эквивалентность с исходной СДНФ для подтверждения корректности преобразования.
Что такое СДНФ и КНФ?
СДНФ (сокращенное дизъюнктивное нормальное форма) и КНФ (конъюнктивное нормальное форма) - это две основные формы представления логических функций. СДНФ представляет функцию в виде суммы произведений литералов, где каждое произведение соответствует одному набору значений, при которых функция истинна. КНФ, напротив, представляет функцию в виде произведения сумм, где каждое слагаемое соответствует одному набору значений, при которых функция ложна.



