Наше приложение поможет тебе разобраться с основами математики - делением с остатком и столбиковой проверкой. Путем простой методики, мы покажем тебе, что решение сложных задач может быть легким и интуитивным процессом.
Включив свою воображение и заставив мозг работать на полную мощность, ты сможешь покорить самые неприступные математические горы. Наш подход основан на тщательно разработанном алгоритме, который поможет тебе решить любую задачу с минимальным количеством усилий.
Мы уверены, что после изучения этого пособия, ты сможешь воспользоваться нашими инструментами для применения новых знаний в повседневной жизни. Ведь математика - неотъемлемая часть нашего мира, и знание правил деления с остатком и столбиковой проверки поможет тебе не только в школе, но и во всех сферах жизни, где возникает необходимость в логическом мышлении и решении сложных проблем.
Концепция деления с остатком: принцип и способы выполнения

Раздел "Что такое деление с остатком и как его выполнить" представляет общую идею этого математического процесса без использования конкретных определений. В этом разделе мы рассмотрим принцип деления с остатком и различные способы его выполнения, используемые для разрешения разнообразных задач.
Концепция деления с остатком представляет собой математический метод, в котором одно число, называемое делимым, делится на другое число, называемое делителем, с получением двух результатов: частного и остатка. Частное представляет собой результат деления без остатка, а остаток - необработанную часть, оставшуюся после деления.
В данном разделе мы рассмотрим два основных способа выполнения деления с остатком - метод долей и метод последовательного вычитания. Метод долей основан на принципе разделения делимого на равные части, а метод последовательного вычитания - на поэтапном вычитании делителя из делимого до тех пор, пока остаток не станет меньше делителя.
Знание и понимание этих методов позволят успешно решать задачи, связанные с делением с остатком, и обеспечат надежную основу для более сложных математических операций.
Основные принципы вычисления с остатком

В данном разделе мы рассмотрим основные принципы и правила, которые помогут вам успешно выполнять операции деления с остатком. Познакомимся с важными понятиями и методами, которые позволят вам правильно проводить вычисления и контролировать полученные результаты.
Перед началом работы нам необходимо уяснить, что деление с остатком – это процесс нахождения частного и остатка в результате деления одного числа на другое. Чтобы достичь успешного результата, важно уметь разбираться в особенностях этой операции и применять соответствующие правила.
Один из ключевых моментов в выполнении деления с остатком – это выбор правильной стратегии вычислений. Существует несколько методов, каждый из которых может быть применим в зависимости от конкретной задачи. Мы рассмотрим наиболее распространенные и покажем, как применять их в практике.
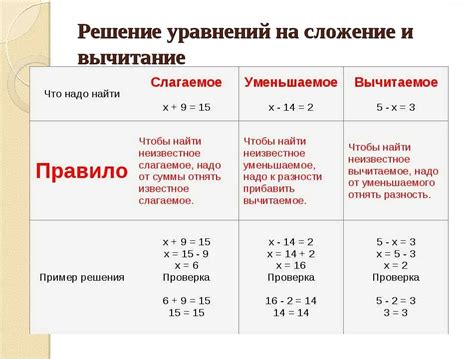
Также, важным аспектом является контроль полученного результата. Для этого можно использовать метод столбиковой проверки, который позволяет убедиться в правильности выполнения операции деления с остатком. Мы рассмотрим этот метод подробно и пошагово объясним его применение.
Все эти правила и методы являются основой для успешного решения задач, связанных с делением с остатком. Понимание и применение этих принципов помогут вам повысить точность и эффективность вашей работы.
Алгоритм вертикального контроля при делении с остатком

В данном разделе рассмотрим эффективный метод проверки правильности выполнения деления с остатком. Алгоритм столбиковой проверки основан на использовании вертикальных вычислений и позволяет убедиться в корректности полученного результата.
Процесс вертикального контроля включает в себя последовательное сравнение и сложение цифр, полученных при делении с остатком. Используя дополнительные операции, такие как вычитание и умножение, можно установить, верно ли выполнено деление или требуется внести корректировки.
Алгоритм столбиковой проверки при делении с остатком может быть особенно полезен при решении математических задач, где требуется точность и надежность результата. Использование этого метода помогает исключить ошибки при выполнении сложных действий с числами и позволяет избежать проблем, связанных с округлением и неучтенными десятичными знаками.
Опираясь на правила столбикового контроля, можно получить точный и надежный ответ при делении с остатком. Алгоритм, хотя и требует определенного времени и внимания, является достаточно простым для понимания и применения. Последовательное выполнение этапов вертикального контроля гарантирует разрешение возможных неточностей и предоставляет достоверный результат.
Подготовка чисел к делению: простые и сложные случаи

Раздел "Подготовка чисел к делению: простые и сложные случаи" представляет собой детальное руководство по подготовке чисел перед их делением, анализируя как простые, так и более сложные случаи. В этом разделе мы рассмотрим общие принципы и стратегии, которые помогут вам успешно решать задачи связанные с делением чисел.
Перед тем как приступить к делению, важно уделить внимание подготовительным шагам. Раздел будет охватывать способы упрощения чисел для более эффективного и точного деления. Он будет включать в себя использование делителей и факторизации чисел, а также дополнительных стратегий для больших и более сложных чисел.
В разделе будут представлены примеры и практические советы по выбору наиболее подходящих техник подготовки чисел для каждого конкретного случая деления. Мы также рассмотрим как обрабатывать числа с десятичной частью и нестандартные ситуации, подробно объясняя стратегии, которые помогут в решении подобных задач.
| Пример простого случая | Пример сложного случая |
|---|---|
| Число: 36 | Число: 583 |
| Делитель: 9 | Делитель: 16 |
| Результат: 4 | Результат: 36 |
Практические примеры для закрепления материала
Для того чтобы лучше понять и научиться применять основы деления с остатком и столбиковой проверки, полезно решать практические задачи. В данном разделе мы представляем несколько примеров, которые помогут вам закрепить материал и улучшить навыки в решении задач.
Ниже приведены простые и понятные задачи, которые можно решать пошагово, используя правила деления с остатком и столбиковую проверку. Метафорические примеры и аналогии также помогут вам лучше понять суть задачи и решить ее правильно. Каждая задача сопровождается подробным объяснением, а также примерами иллюстраций, которые помогут вам визуализировать процесс решения.
Задача №1: Распределение яблок
Вася купил 12 яблок и хочет поделить их поровну между собой и своими двумя друзьями. Сколько яблок достанется каждому?
Задача №2: Продажа конфет
Екатерина продает конфеты, а каждая коробка вмещает по 20 штук. Если у нее есть 56 конфет, сколько коробок она сможет собрать?
Задача №3: Доставка посылок
Для доставки посылок используются грузовики, в каждом из которых может поместиться 34 посылки. Если имеется 150 посылок, сколько грузовиков понадобится для доставки?
Решая данные задачи и другие подобные примеры, вы не только укрепите свое понимание правил деления с остатком и столбиковой проверки, но и развиваете логическое мышление и аналитические способности. Более тщательное прочтение и практика решения упражнений помогут вам стать более уверенным в решении сложнее задач в будущем.
Ошибки, которые рекомендуется избегать при выполнении деления по модулю

При выполнении деления по модулю существуют некоторые распространенные ошибки, которые важно избегать. В этом разделе мы рассмотрим эти ошибки и предоставим рекомендации по их устранению.
- Исключение деления на ноль
- Неучет отрицательных значений и знака остатка
- Неверное округление
- Неправильное использование оператора деления
- Неучет ограничений типов данных
Одной из распространенных ошибок при делении по модулю является деление на ноль, что приводит к неопределенному результату. Важно всегда проверять, что делитель не равен нулю, чтобы избежать подобных ошибок.
Эта ошибка происходит, когда при делении по модулю отрицательного числа или целого числа со знаком не учитывается знак остатка. Для правильной работы с отрицательными значениями необходимо учитывать правило знака остатка и применять его к результатам.
Иногда происходит неверное округление при делении по модулю, что может привести к неточным результатам. Рекомендуется всегда проверять используемые алгоритмы округления и учитывать их особенности в конкретной задаче.
Очень важно правильно использовать оператор деления при выполнении деления по модулю. Некорректное использование оператора может привести к непредсказуемым результатам и ошибкам в расчетах. Важно внимательно изучить и понять правила использования оператора деления в конкретном языке программирования или среде.
При выполнении деления по модулю необходимо учитывать ограничения типов данных, с которыми работает программа. Некорректное использование типов данных может привести к переполнению и неправильным результатам. Важно всегда проверять, что используемые типы данных соответствуют ожидаемым значениям и ограничениям.
Ситуации, требующие особого внимания при делении на двузначные и многозначные числа
В процессе деления на двузначные и многозначные числа могут возникать сложные ситуации, требующие дополнительного внимания и аккуратного решения. Понимание особенностей этих ситуаций позволит более эффективно и точно выполнять деление с остатком.
Одним из таких случаев является деление числа, которое является меньшим, чем делитель. В такой ситуации результатом деления будет натуральное число, а остаток будет равен исходному числу. Например, при делении числа 25 на число 60 результатом будет 0, а остаток также будет равен 25.
Еще одной сложной ситуацией может быть деление на число, которое является больше исходного числа. В этом случае результатом деления будет 0, а остаток будет равен исходному числу. Например, при делении числа 39 на число 100 результатом будет 0, а остаток также будет равен 39.
Другой важной ситуацией является деление числа, у которого цифры в разрядах меньше разрядов делителя. В таком случае следует умножить исходное число на 10 или другую степень 10, чтобы привести его к уровню делителя. Например, при делении числа 69 на число 200 следует умножить 69 на 10, чтобы получить 690, и только затем выполнять деление.
Оптимизация процесса деления с остатком для более эффективного решения задач

В данном разделе рассмотрим методы, которые могут быть применены для упрощения процесса деления с остатком. Они помогут ускорить решение задач и повысить эффективность работы.
1. Предварительная оценка остатка: перед выполнением деления, рекомендуется оценить возможный остаток исходного числа. Это позволяет выбрать оптимальный способ деления и сэкономить время на лишних вычислениях.
2. Применение математических свойств: для упрощения процесса деления можно использовать различные алгоритмические и математические свойства, такие как свойства делимости чисел, правила умножения и сложения.
3. Использование аналогий и схожих задач: при решении задач по делению с остатком, полезно обращаться к ранее решенным аналогичным задачам. Это позволяет применить уже известные методы и легко получить результат.
4. Разбиение числа на части: вместо деления всего числа можно разбить его на более мелкие части, которые будут проще обрабатываться. Затем полученные результаты можно будет объединить и получить итоговое значение.
5. Интуитивные подходы: иногда, при решении задач по делению с остатком, полезно довериться своей интуиции и использовать разнообразные приемы, несмотря на их нестандартность. Это может привести к более быстрому и эффективному решению.
Сочетание этих методов и их грамотное применение могут значительно упростить процесс деления с остатком и ускорить решение задач. Они позволяют найти оптимальный путь, минимизируя количество вычислений и повышая точность полученных результатов.
Вопрос-ответ

Какие правила деления с остатком существуют и как их применять?
Существуют два правила деления с остатком: правило с остатком и правило с неполным частным. Чтобы воспользоваться правилом с остатком, необходимо поделить делимое на делитель и записать остаток. Правило с неполным частным применяется, когда не получается поделить число нацело и приходится оставить частичное значение. Для правила с неполным частным используется столбиковая запись. Поделить делитель на делимое и записать частное с остатком.
Как применить столбиковую проверку при делении с остатком?
Для применения столбиковой проверки при делении с остатком необходимо записать делимое и делитель в столбик. Затем, последовательно производить действия над цифрами в столбиках: вычитание, деление и умножение, чтобы получить частное и остаток. Результат проверки должен быть равен делимому.
Какие ошибки часто возникают при решении задач по делению с остатком?
При решении задач по делению с остатком часто возникают такие ошибки: неправильная запись делимого и делителя в столбик, неправильное выполнение вычитания, деления и умножения в рамках столбиковой проверки, неправильное определение частного и остатка. Важно внимательно следить за каждым шагом и правильно выполнять все действия.