Разбираясь в особенностях создания регрессионной модели, необходимо не только понимать ее принципы, но и быть готовым к освоению широкого спектра терминов и подходов данной области.
В данной статье мы собираемся представить вам полное руководство по построению линейной регрессионной модели - метода, который является одним из основных инструментов анализа и предсказания. Здесь вы найдете все необходимые шаги и техники, начиная от выбора зависимой переменной и набора данных, до оценки качества модели и интерпретации результатов.
Наша цель - облегчить вам путь к пониманию этого сложного, но увлекательного процесса. Мы избегаем сложных технических терминов вроде "регрессия" и "функция", заменяя их более простыми и понятными словами. Мы покажем, как построить качественную модель, на примере различных задач и реальных данных.
Основы построения регрессионной модели: ключевые принципы и концепции

Важным аспектом построения регрессионных моделей является выбор адекватных, репрезентативных данных для анализа. Мы рассмотрим различные методы сбора данных и стратегии выбора обучающей выборки, чтобы гарантировать точность и достоверность наших результатов.
- Один из ключевых принципов регрессионного моделирования - это линейность. Мы изучим, как и почему линейная функция используется в регрессионной модели и как она помогает нам предсказывать зависимые переменные на основе независимых.
- Важно также понимать концепцию мультиколлинеарности, когда независимые переменные в модели взаимосвязаны между собой. Мы рассмотрим, как определить и устранить мультиколлинеарность, чтобы получить более точные и интерпретируемые результаты.
- Другим важным аспектом регрессионного моделирования является оценка качества модели. Мы изучим различные метрики и подходы для измерения точности и эффективности наших моделей, а также способы их интерпретации.
- Наконец, мы рассмотрим ключевые принципы и концепции регуляризации, которые помогают преодолеть проблему переобучения моделей и повысить их обобщающую способность.
Понимание основных принципов и концепций построения регрессионных моделей позволит вам успешно анализировать данные, прогнозировать результаты и принимать более информированные решения на основе полученных результатов.
Обзор понятия регрессии и ее применение в моделях
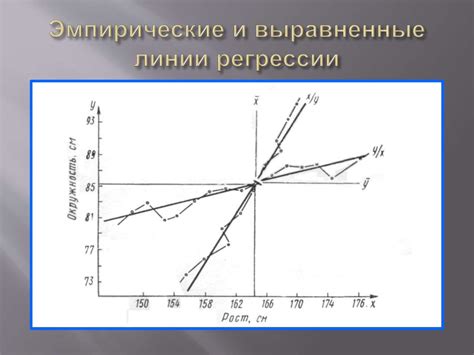
Регрессионные модели основаны на линейной функции, которая представляет собой простейшую форму зависимости между переменными. Линейная функция представлена уравнением Y = α + βX , где Y - значение зависимой переменной, X - значение независимой переменной, α - сдвиг по оси Y (интерсепт), β - коэффициент наклона (slope), определяющий величину изменения Y при изменении X на единицу. Основная идея линейной регрессии заключается в поиске оптимальных значений коэффициентов α и β, чтобы минимизировать разницу между фактическими и предсказанными значениями. Для этого в моделировании используется метод наименьших квадратов, который помогает оценить параметры линейной функции с наименьшей суммой квадратов ошибок.
Для оценки качества построенной модели используются различные метрики, такие как R-квадрат, средняя абсолютная ошибка (MAE), средняя квадратичная ошибка (MSE) и др. Более точные значения метрик указывают на лучшую адаптацию модели к данным, а значит, более точные предсказания. Регрессионные модели могут быть расширены с использованием нелинейных функций, включая полиномиальные, логарифмические, экспоненциальные и другие, чтобы лучше аппроксимировать реальные данные и улучшить качество предсказаний.
| Преимущества регрессионных моделей: | Недостатки регрессионных моделей: |
|---|---|
| - Относительная простота и интерпретируемость | - Чувствительность к выбросам и нелинейным зависимостям в данных |
| - Широкое применение и понятность для бизнес-аналитиков | - Ограничение на линейную зависимость между переменными |
| - Возможность предсказывать значения зависимой переменной | - Потребность в достаточном объеме качественных данных |
Роль линейной функции в построении регрессионных моделей
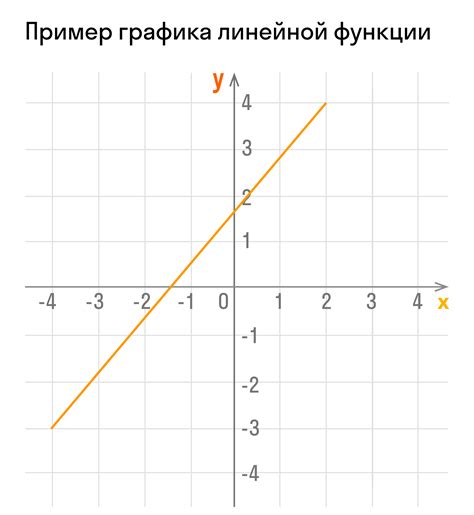
В данном разделе мы рассмотрим, как линейная функция играет важную роль в создании и анализе регрессионных моделей. Подробно разберем принципы ее использования и покажем, как она помогает в определении связей и зависимостей между переменными.
Линейная функция, как основной инструмент в регрессионном анализе, позволяет определить, насколько одна переменная изменяется при изменении другой переменной. Она описывает прямую зависимость между ними, что позволяет предсказывать значения одной переменной на основе другой. Используя линейную функцию в регрессионной модели, мы можем оценить влияние каждого параметра и провести анализ силы связи между ними.
Линейная функция обладает свойством простоты и наглядности, что делает ее широко применимой в регрессионном анализе. Она представляет собой линию, которая наилучшим образом приближает значения нашего датасета и позволяет сделать прогнозы для новых данных. Это основа для построения регрессионной модели, которая помогает нам понять и предсказать связи между переменными и принять обоснованные решения на основе этих связей.
Применение линейной функции в регрессионных моделях требует анализа качества подгонки данных к модели и интерпретации полученных коэффициентов. Также важным аспектом является оценка значимости и статистической достоверности связи между переменными. Благодаря линейной функции мы имеем возможность объяснить, предсказать и контролировать взаимосвязи в данных, что делает ее незаменимой в регрессионном анализе.
Правильный выбор функции: фундамент успешного моделирования данных

Важность правильного выбора функции при построении регрессионной модели составляет основу успешного моделирования данных. Выбор подходящей функции позволяет достичь оптимальной точности прогнозирования и интерпретируемости результатов.
Адекватное моделирование: Процесс выбора правильной функции должен учитывать специфику и особенности данных, а также цель моделирования. Необходимо стремиться к тому, чтобы функция была адекватной с точки зрения изучаемого явления и имела смысловую интерпретацию.
Линейная и нелинейная модель: Наиболее распространенным выбором является линейная функция, однако не следует забывать о возможности использования нелинейных функций. Нелинейные модели могут лучше описывать зависимости в данных и предсказывать их поведение вне исходной обучающей выборки.
Выбор функциональной формы: Помимо выбора между линейной и нелинейной моделью, необходимо также определить функциональную форму выбранной модели. Различные функции могут выражать разные формы зависимостей, такие как полиномиальные, экспоненциальные или логарифмические. Выбор функциональной формы должен быть обоснован эмпирическими исследованиями и предварительным анализом данных.
Сравнение и оценка моделей: Важным этапом процесса выбора функции является сравнение и оценка различных моделей. Это позволяет определить, какая из моделей лучше соответствует данным и достигает наилучшего уровня точности прогнозирования. Для этого можно использовать различные метрики оценки, такие как средняя квадратичная ошибка, коэффициент детерминации и другие.
В итоге, правильный выбор функции для моделирования данных играет ключевую роль в достижении точности прогнозирования и понимании зависимостей в данных. Важно учитывать специфику данных, стремиться к адекватному моделированию и проводить сравнение и оценку различных моделей, чтобы выбрать оптимальную функцию для конкретной задачи.
Подготовка данных и формирование выборки для анализа

Первоначально необходимо проанализировать доступные данные и их качество: проверить их полноту, точность и достоверность. Также, важно установить наличие пропущенных значений и выбросов, а при необходимости, провести их обработку. Важно отметить, что результаты моделирования будут значительно искажены, если данные содержат аномалии или пропущенные значения.
После подготовки данных, следующим шагом является выборка – отбор нужной части данных для анализа. Важно правильно выбрать размер выборки и определить критерии выбора. Виды выборки могут варьироваться в зависимости от задачи и доступных данных: случайная выборка, систематическая выборка, стратифицированная выборка и другие.
Подготовка данных и формирование выборки являются ключевыми основами для построения регрессионной модели на основе линейной функции. Тщательная работа на этом этапе может существенно повысить точность и надежность моделирования, что в свою очередь даст более достоверные результаты и более точные прогнозы.
Предварительная подготовка данных для работы с аналитическими моделями

Сбор данных
Первым шагом является сбор данных, необходимых для работы с регрессионными моделями. Это может включать в себя поиск источников данных, проведение опросов, анализ уже существующих данных и многое другое. Главная цель данного этапа - получение полного и достоверного набора данных для последующего анализа.
Очистка данных
После сбора данных необходимо провести их очистку от ошибок, пропусков и выбросов. В этом случае могут использоваться различные методы, такие как удаление или замена некорректных значений, агрегация данных и проверка на наличие дубликатов. Целью данного этапа является создание чистого и однородного набора данных, на котором можно будет строить регрессионную модель.
Преобразование данных
Иногда данные требуют преобразования перед использованием их в регрессионной модели. Это может включать в себя изменение масштаба переменных, создание новых признаков на основе существующих или применение других методов, которые делают данные более подходящими для регрессионного анализа. Правильное преобразование данных может значительно повысить результаты работы с моделью.
Как подобрать подходящую выборку для построения модели: секреты успешного регрессионного анализа

Важно учитывать не только количество данных, но и их качество. Ошибочно предполагать, что чем больше данных, тем лучше будет модель. Подходящая выборка должна отражать различные аспекты и вариации изучаемого явления, чтобы учесть все факторы, влияющие на целевую переменную.
Прежде чем приступить к сбору данных, необходимо провести анализ потенциальных источников выборки. Не стоит ограничиваться только общедоступными базами данных, ведь они могут быть неактуальными или содержать ограниченное количество основных параметров.
Выборка должна быть репрезентативной, что означает, что она должна быть представительной для генеральной совокупности, которую вы хотите исследовать. Необходимо учесть разнообразность возраста, пола, социального статуса и других факторов, связанных с вашим объектом исследования.
Внимательный и основательный анализ выборки - залог успешного регрессионного анализа. С учетом всех вышеизложенных факторов и соблюдением соответствующих принципов, вы сможете построить модель, которая точно отражает зависимости между переменными и обладает высокой предсказательной способностью.
Исследование и оценка линейной модели
Исследование
Прежде чем приступить к оценке модели, необходимо провести исследование данных. Это включает анализ структуры данных, выявление выбросов и пропущенных значений, а также определение зависимой переменной и независимых переменных, которые будут использованы для построения модели.
Важной частью исследования является выбор подходящей линейной функции, которая будет определять отношения между независимыми переменными и зависимой переменной. Можно использовать различные модели, такие как простая линейная регрессия, множественная линейная регрессия или полиномиальная регрессия, в зависимости от характера исследуемых данных.
Оценка качества модели
После построения модели необходимо оценить ее качество. Для этого используются различные статистические метрики, которые позволяют понять, насколько хорошо модель описывает имеющиеся данные. Некоторые из наиболее распространенных метрик включают среднеквадратичную ошибку (MSE), коэффициент детерминации (R-квадрат) и среднюю абсолютную ошибку (MAE).
Оценка модели также включает проведение статистических тестов на значимость коэффициентов регрессии. Это позволяет определить, насколько надежными и статистически значимыми являются полученные результаты. Также важным аспектом оценки модели является анализ остатков, которые представляют собой разницу между фактическими значениями зависимой переменной и значениями, предсказанными моделью. Анализ остатков помогает оценить точность модели и выявить наличие систематических ошибок.
В данном разделе статьи мы подробно рассмотрим каждый этап исследования и оценки линейной модели, а также представим практические примеры и рекомендации по выбору наиболее подходящей модели и методов оценки ее качества.
Шаги построения модели: от выбора переменных до получения результатов

Исследование зависимости
В данном разделе рассмотрим важные этапы процесса построения регрессионной модели на основе линейной функции. Мы изучим, как выбрать наиболее значимые переменные, провести анализ данных и определить статистическую связь между ними. На основе этого анализа мы сможем построить модель, которая наиболее точно описывает зависимость и предсказывает значения целевой переменной.
Шаг 1: Подготовка данных
На этом этапе необходимо собрать данные и провести их предварительную обработку. Мы должны убедиться, что данные корректны, осуществить очистку от выбросов и пропущенных значений. Затем нам потребуется провести разведочный анализ, чтобы лучше понять распределение переменных и возможные взаимосвязи.
Шаг 2: Выбор переменных
На этом шаге мы определим, какие переменные следует включить в модель. Мы будем искать те, которые имеют сильную корреляцию с целевой переменной и вносят дополнительную информацию в модель. При этом мы должны учитывать мультиколлинеарность – ситуацию, когда независимые переменные сильно коррелируют друг с другом.
Шаг 3: Построение модели
На этом этапе мы задаем линейную функцию, которая описывает зависимость между переменными. Мы должны определить коэффициенты модели с помощью метода наименьших квадратов. При этом необходимо учесть предположения о нормальности распределения ошибок и отсутствии автокорреляции в остатках.
Шаг 4: Проверка модели
На данном шаге мы проводим анализ остатков модели, чтобы проверить ее адекватность. Мы будем оценивать значимость коэффициентов, проводить тесты на гомоскедастичность и нормальность распределения остатков. Если модель не удовлетворяет требованиям, мы должны провести коррекцию и повторить шаги 3 и 4.
Шаг 5: Получение результатов
Метрики оценки качества моделей: выбор наиболее подходящих показателейУлучшение и оптимизация предсказательной модели: путь к более точным результатам


После построения первоначальной предсказательной модели на основе линейной функции, возникает необходимость улучшить и оптимизировать ее, чтобы получить более точные и репрезентативные результаты. В данном разделе будет рассмотрено несколько методов и подходов к улучшению модели, которые помогут достичь этой цели.
- Методы отбора признаков: одним из способов улучшения модели является анализ и выбор наиболее значимых признаков, которые наиболее сильно влияют на целевую переменную. Это позволяет устранить шум в данных и сосредоточиться на ключевых влияющих факторах.
- Использование полиномиальных признаков: часто линейная функция не в состоянии полностью описать сложные взаимосвязи между признаками. Добавление полиномиальных признаков может помочь учесть эти сложности и улучшить точность модели.
- Регуляризация: для предотвращения переобучения модели можно использовать методы регуляризации, такие как L1 и L2 регуляризация. Эти методы помогают контролировать сложность модели и избежать переобучения, улучшая ее обобщающую способность.
- Нормализация данных: важным шагом в оптимизации модели является нормализация данных, чтобы привести их к общему диапазону значений. Это позволяет избежать проблемы с масштабированием и несбалансированными весами признаков.
- Кросс-валидация: для оценки производительности модели и выбора оптимальных параметров, можно использовать кросс-валидацию. Этот подход позволяет более надежно оценивать модель, учитывая ее поведение на различных подмножествах данных.
Применение данных методов и подходов к улучшению и оптимизации предсказательной модели на основе линейной функции позволяет получить более точные и надежные результаты. Однако стоит помнить, что каждая модель требует индивидуального подхода, и выбор конкретных методов зависит от характера данных и целей исследования.
Методы формирования признаков для улучшения эффективности модели

| Метод | Описание |
|---|---|
| Добавление полиномиальных признаков | Путем возведения исходных признаков в степень мы можем учесть нелинейную зависимость между переменными, улучшив качество модели. |
| Преобразование признаков | Применение различных математических функций (например, логарифмирование, возведение в степень, экспоненциальное преобразование) может помочь нормализовать данные и улучшить их интерпретируемость. |
| Интерактивные признаки | Путем создания новых признаков на основе комбинаций уже существующих мы можем учесть сложные взаимодействия между переменными, что может привести к лучшему предсказанию. |
| Удаление выбросов и работа с пропущенными значениями | Очистка данных от выбросов и эффективное управление пропущенными значениями позволит снизить шум и улучшить процесс обучения модели. |
| Нормализация признаков | Приведение масштабов признаков к единому диапазону поможет справиться с проблемой разных единиц измерения, а также повысит стабильность обучения модели. |
| Отбор наиболее значимых признаков | Анализ важности признаков позволит отбросить неинформативные переменные, ускорив обучение модели и улучшив ее предсказательную способность. |
Применение данных методов позволит нам получить оптимальную модель, способную точно предсказывать целевую переменную на основе линейной функции и учитывать сложные зависимости между признаками.
Вопрос-ответ

Какие данные нужны для построения регрессионной модели на основе линейной функции?
Для построения регрессионной модели на основе линейной функции необходимо иметь набор данных, состоящий из зависимой переменной и одной или нескольких независимых переменных. Зависимая переменная должна быть количественной, а независимые переменные - числовыми или категориальными.
Какой метод использовать для построения регрессионной модели на основе линейной функции?
Для построения регрессионной модели на основе линейной функции можно использовать метод наименьших квадратов. Этот метод позволяет минимизировать сумму квадратов разностей между фактическими значениями зависимой переменной и значениями, предсказанными моделью.
Как оценить качество построенной регрессионной модели на основе линейной функции?
Оценка качества построенной регрессионной модели на основе линейной функции может быть выполнена с помощью таких показателей, как коэффициент детерминации (R-квадрат) и среднеквадратичная ошибка (MSE). R-квадрат показывает, насколько хорошо модель объясняет вариацию зависимой переменной, а MSE измеряет разницу между фактическими значениями и предсказаниями модели.
Какие предположения делаются при построении регрессионной модели на основе линейной функции?
При построении регрессионной модели на основе линейной функции делаются следующие предположения: линейность зависимости между независимыми и зависимой переменными, отсутствие автокорреляции ошибок, нормальность распределения ошибок и отсутствие мультиколлинеарности между независимыми переменными.
Можно ли использовать регрессионную модель на основе линейной функции для прогнозирования значений зависимой переменной?
Да, регрессионная модель на основе линейной функции может быть использована для прогнозирования значений зависимой переменной. После построения модели можно подставить значения независимых переменных и получить предсказанные значения зависимой переменной.
Как построить регрессионную модель на основе линейной функции?
Для построения регрессионной модели на основе линейной функции необходимо провести анализ данных, определить зависимую и независимые переменные, подобрать математическую формулу линейной функции, выполнить оценку параметров и провести проверку адекватности модели. В статье подробно описывается все этапы данного процесса.




