В мире бизнеса и науки данные являются неотъемлемой частью процессов принятия решений и исследований. Однако, важно не только уметь собирать и анализировать данные, но и уметь представить их результаты в удобной и понятной форме. В этом контексте регрессия, как инструмент статистического анализа, является одним из важнейших средств для моделирования и прогнозирования различных явлений и процессов.
Успешное применение регрессии требует не только хорошего понимания методологии и принципов работы с данными, но и умения сохранить результаты после Международного сотрудничества по экономической кооперации (МСЭК). Это обеспечит сохранение ценной информации и возможность повторного использования результатов исследования.
В данной статье мы рассмотрим основные аспекты оформления регрессии и методы сохранения результатов после МСЭК. Будут рассмотрены практические советы по выбору и оформлению моделей, работе с переменными, обработке выбросов и выбору релевантных факторов. Также будет рассмотрен вопрос сохранения результатов в различных форматах, а также оптимальных способов их представления для дальнейшей интерпретации и анализа.
Важность правильного оформления и интерпретации результатов регрессии в психологическом исследовании

При оформлении результатов регрессии необходимо следовать установленным нормам и рекомендациям. Важно представить таблицу с описательными статистиками для всех переменных, включая средние значения, стандартные отклонения и корреляции между ними. Далее следует представить таблицу с коэффициентами регрессии, где указываются оценки для каждого фактора и константы. Коэффициенты регрессии следует сопровождать p-значениями и доверительными интервалами для оценки статистической значимости.
- Применение диаграмм рассеяния помогает визуализировать взаимосвязь между переменными и наглядно представить результаты регрессии. Создание графиков, на которых отображаются наблюдаемые данные и линия регрессии, может быть полезным способом представления результатов исследования.
- Также важно тщательно интерпретировать результаты регрессии. Коэффициенты регрессии отражают величину и направление влияния факторов на зависимую переменную. Но помимо этого, необходимо также учитывать значимость коэффициентов и их практическую значимость в конкретной области исследования.
Правильное оформление и интерпретация результатов регрессии играют важную роль в психологическом исследовании. Они позволяют более точно понять и объяснить отношения между переменными и принимать обоснованные решения на основе полученных результатов.
Понятие регрессии и его применение в психологических исследованиях

В психологии регрессия применяется для исследования различных факторов, оказывающих влияние на человеческое поведение, эмоции или мышление. Например, с помощью регрессионного анализа можно определить, какие факторы способствуют развитию депрессии у определенной группы людей, или какие переменные влияют на эффективность определенного метода психотерапии.
Основной целью регрессионного анализа является выявление сильных или слабых связей между переменными, а также определение важности каждой из них при предсказании психологических или поведенческих результатов. Например, путем использования регрессионного анализа можно выяснить, что уровень образования и доход являются сильными предикторами уровня удовлетворенности работой. Также регрессионный анализ может быть полезен для выявления групп людей, которые наиболее подвержены развитию определенных психологических состояний или поведенческих расстройств.
Подходы к регрессионному анализу в психологических исследованиях могут варьироваться в зависимости от целей исследования. Использование различных методов, таких как множественная регрессия, иерархическая регрессия или логистическая регрессия, позволяет более точно изучать связи между переменными и создавать более надежные модели предсказания психологических и поведенческих исходов.
Таким образом, регрессия представляет собой эффективный инструмент, который позволяет психологам изучать и предсказывать различные аспекты человеческого поведения и психологических состояний. Понимание основ регрессии и ее применение в психологических исследованиях помогает улучшить понимание факторов, влияющих на нашу психику и помогает разработать более эффективные стратегии работы с пациентами и клиентами.
Этапы разработки регрессионной модели в исследовательской работе
При проведении исследования, направленного на анализ зависимости между переменными, необходимо разработать регрессионную модель. Оформление данной модели включает несколько этапов, которые позволяют получить достоверные и полезные результаты.
- Определение целевой переменной
- Выбор независимых переменных
- Сбор данных
- Анализ данных
- Построение модели
- Оценка и интерпретация модели
Первым этапом разработки регрессионной модели является определение целевой переменной. Целевая переменная является зависимой, исследуемой величиной, которую необходимо предсказать или объяснить с помощью независимых переменных.
После определения целевой переменной следует выбор независимых переменных, которые могут оказывать влияние на целевую переменную. Независимые переменные должны быть измеримыми и релевантными для исследуемой проблематики.
На данном этапе необходимо собрать данные, которые будут использованы для построения регрессионной модели. Данные могут быть получены из различных источников, таких как наблюдения, эксперименты, опросы и т.д. Важно обеспечить качество и достоверность данных.
После сбора данных следует их анализ. Включает в себя описание исходных данных, проверку на пропущенные значения и выбросы, а также исследование статистических связей между переменными.
На основе предыдущих этапов можно приступить к построению регрессионной модели. Задача состоит в нахождении математической функции, которая описывает зависимость между независимыми и целевой переменными. В результате данного этапа получается уравнение регрессии.
После построения модели необходимо оценить ее качество и провести интерпретацию результатов. Для оценки используются различные метрики, такие как среднеквадратическая ошибка, коэффициент детерминации и другие. Результаты модели могут быть интерпретированы с учетом статистической значимости и важности независимых переменных.
Таким образом, разработка регрессионной модели в исследовательской работе проходит через ряд этапов, начиная с определения целевой переменной и выбора независимых переменных, и заканчивая оценкой и интерпретацией модели. Каждый этап играет важную роль в получении достоверных и полезных результатов исследования.
Выбор оптимальной модели регрессии для анализа данных
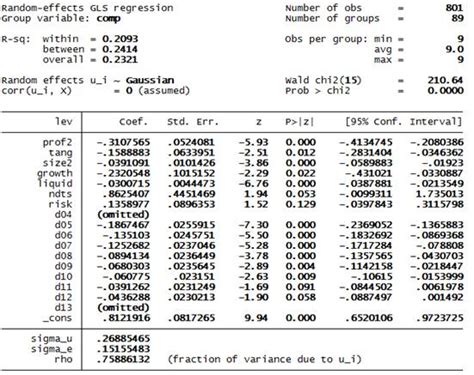
Когда мы анализируем данные и строим модель регрессии, важно выбрать подходящую модель, которая наиболее точно отражает общую зависимость между переменными. Это позволяет нам делать прогнозы и понимать, как одна переменная влияет на другую. Однако, существует множество различных моделей регрессии, и выбор оптимальной модели может быть сложной задачей.
При выборе модели регрессии необходимо учитывать множество факторов, таких как:
- Тип зависимой переменной
- Количество независимых переменных
- Предположения, которые должна удовлетворять модель
- Наличие взаимодействий между переменными
- Учет нелинейных зависимостей
Каждая модель регрессии имеет свои преимущества и ограничения, и выбор оптимальной модели требует анализа данных и применения статистических методов. Некоторые из наиболее популярных моделей регрессии включают линейную регрессию, полиномиальную регрессию, логистическую регрессию и регрессию с временными рядами. В зависимости от конкретной задачи и особенностей данных, одна модель может быть более предпочтительной, чем другая.
Для выбора оптимальной модели регрессии можно использовать различные методы, такие как анализ регрессии, кросс-валидация, информационные критерии и сравнение различных моделей по их статистическим показателям. Важно учитывать как качество предсказания модели, так и интерпретируемость ее коэффициентов.
В итоге, выбор подходящей модели регрессии для анализа данных является важным шагом, который влияет на точность прогнозов и понимание зависимости переменных. Необходимо тщательно изучить данные, учитывая различные факторы, и применить соответствующие статистические методы для определения наилучшей модели.
Статистическая значимость регрессионных коэффициентов и их толкование

Для определения значимости регрессионных коэффициентов используются различные статистические методы, такие как t-тест или анализ вариации (ANOVA). Они позволяют оценить вероятность случайности взаимосвязи между переменными и помогают исключить ложные или незначимые корреляции.
Интерпретация значимости коэффициентов регрессии основывается на их значениях и направлении связи с зависимой переменной. Положительный коэффициент указывает на прямую пропорциональность между переменными, тогда как отрицательный - на обратную зависимость. Величина коэффициента отражает силу влияния: чем выше абсолютное значение, тем сильнее связь между переменными.
Важно помнить, что множественная регрессия позволяет учесть взаимодействие нескольких независимых переменных и оценить их влияние на зависимую переменную одновременно. Поэтому при интерпретации значимости коэффициентов следует учитывать контекст и взаимосвязь между всеми переменными в модели.
Методы проверки достоверности применимости модели регрессии

В данном разделе мы рассмотрим различные подходы и методы, которые позволяют оценить достоверность и применимость модели регрессии, используемой для анализа данных. Эти методы помогут нам убедиться в адекватности модели и ее способности предсказывать зависимые переменные на основе независимых факторов.
Перекрестная проверка является одним из наиболее распространенных методов проверки моделей регрессии. Она позволяет оценить точность модели с использованием данных, которые не использовались при построении этой модели. Путем разделения доступных данных на обучающую и тестовую выборки, мы можем проверить, насколько хорошо модель обобщает данные и способна предсказывать результаты на новых наблюдениях.
Анализ остатков представляет собой другой метод проверки адекватности моделей регрессии. Важно выяснить, являются ли остатки модели случайными, то есть несут ли они в себе какую-либо дополнительную информацию или закономерность. Это может быть сделано с помощью визуализации остатков, а также с использованием статистических тестов на автокорреляцию и гетероскедастичность.
Интерпретация коэффициентов является еще одним важным аспектом проверки адекватности модели регрессии. Мы должны обратить внимание на значения и знаки коэффициентов, чтобы понять, какие факторы оказывают существенное влияние на зависимую переменную. Иногда может потребоваться статистическая проверка значимости коэффициентов на основе их стандартных ошибок и доверительных интервалов.
Сравнение моделей также может быть полезным методом для проверки адекватности модели регрессии. Мы можем сравнить несколько моделей, используя различные факторы и методы построения, чтобы определить, какая из них лучше соответствует нашим данным и предсказывает зависимую переменную наиболее точно. При этом необходимо учитывать различные критерии оценки, такие как коэффициент детерминации, информационные критерии, а также экономическую и практическую интерпретацию результатов.
Когда мы говорим о регрессионных анализах, мы рассматриваем связь между зависимой и независимыми переменными. Однако, для полного и точного понимания этих результатов, необходимо учитывать широкий контекст, включающий в себя медицинские, социальные, психологические и другие аспекты исследуемой проблемы. МСЭК предоставляет возможность проанализировать полученные данные с участием экспертов разных областей знания и определить, какие факторы могут оказать влияние на регрессионные результаты. Таким образом, учет рекомендаций МСЭК становится важным при интерпретации этих результатов.
При использовании результатов МСЭК в процессе интерпретации регрессионных анализов, важно учесть, что они могут помочь увидеть более широкую картину исследуемой проблемы. Например, МСЭК может предоставить дополнительную информацию о факторах, которые не были учтены в исходном исследовании, но могут оказать значительное влияние на полученные результаты. Такой подход позволяет сделать интерпретацию более релевантной и основанной на всестороннем анализе доступной информации.
Применение результатов регрессионного анализа в последующих исследованиях

Для сохранения результатов регрессионного анализа можно применить различные методы и техники. Один из наиболее распространенных способов - создание таблицы, в которой приведены ключевые показатели, коэффициенты регрессии и их значимость. Такая таблица позволяет исследователю быстро ознакомиться с результатами анализа и использовать их в последующих исследованиях.
Дополнительно, результаты регрессионного анализа могут быть представлены в виде графиков или диаграмм, что позволяет наглядно визуализировать взаимосвязи между переменными и выделить основные тренды и изменения. Такой визуальный подход может быть полезен при дальнейшем анализе данных и позволить исследователю более глубоко исследовать связи между переменными.
Результаты регрессионного анализа также могут быть применены при построении прогностических моделей. Используя полученные коэффициенты регрессии и имеющиеся данные, можно разработать модель, которая будет предсказывать значения зависимой переменной на основе независимых переменных. Это позволит сделать прогнозы и оценить вероятные изменения в исследуемой области в будущем.
| Ключевые показатели | Коэффициенты регрессии | Значимость |
|---|---|---|
| Показатель 1 | 0.456 | *** |
| Показатель 2 | 0.123 | *** |
| Показатель 3 | 0.789 | *** |
Вопрос-ответ




