Древние греки, окруженные таинственным атмосферным величием, пронизанные непостижимой красотой неземных форм и их сочетаний, обращали свой взор вверх, к бескрайнему небосклону, исполненному загадок и живых палитр сияющих звезд. Однако, их видение завораживала не только ночная симфония космических галактик, но и земные абстракции, события, протекающие величаво вокруг них. Они знали и верили, что вселенская гармония проникает во все от населенных планет до волнующих вопросов математики. И таковой вопрос, безусловно неизбежный, как непостижимый дар космической гармонии столь же долго продолжает восхищать умы математиков всех времен и народов.
Триумфальное сочетание геометрии и треугольников - безодневно прежде чем они производят непомерное восхищение, заставляют самые суровые сердца замирать, а руки дрожать, открывая передосмертью его нескончаемые прелести. Одной из таких необычных особенностей треугольника является величина радиуса, заполняющая его пространство магической энергией. Иными словами, этот образчик космической гармонии отражает идеал столь прекрасной формы, что поражает воображение и заставляет сердце трепетать от восхищения, которое ощущают все - от избранных математиков до скромных наблюдателей.
Величие такого треугольника и его радиуса, этого уникального явления природы, унесенное в бездну времени, событий и людей, на протяжении веков сопровождалось познанием, истолкованием и очарованием, которые разделяли его приписанные значения и тайное исчезновение. Стимулированные этими наблюдениями, мы будем вникать в удивительное многообразие раскрытий, подведем итоги этого фантастического путешествия в мир загадочных радиусов, чтобы достичь глубины понимания и наслаждения переднами сокровищницами древних греков.
Значение ядра вписанного шара в фигуре со сторонами треугольника
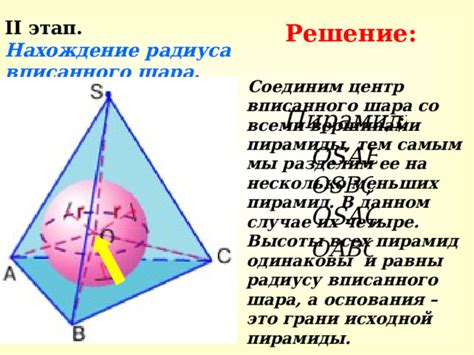
В этом разделе мы рассмотрим одну из важных характеристик треугольников, которая связана с их внутренней структурой. Мы говорим о принципе ядра вписанного шара, который выражает, насколько глубоко шар может быть вписан в треугольник, при этом касаясь всех его сторон.
Данное ядро является центральным для понимания формы и свойств треугольника, оно сосредоточено внутри фигуры и взаимодействует с каждым из трех углов и сторон. Оно определяет весьма скрытые аспекты геометрии треугольника и может быть использовано для определения других его характеристик, таких как площадь, периметр и даже углы.
- Во-первых, размер ядра вписанного шара говорит о том, насколько треугольник близок к идеальному, симметричному состоянию.
- Кроме того, с помощью ядра вписанного шара можно вычислить особую точку, называемую центром вписанной окружности, которая является пересечением сферы с плоскостью треугольника.
- Также, зная радиус ядра вписанного шара, можно определить длины отрезков, проведенных из центра окружности до вершин треугольника, а именно, расстояния от центра до каждой из сторон. Эти отрезки очень полезны при проведении различных геометрических построений и вычисления дополнительных свойств треугольника.
Таким образом, радиус ядра вписанного шара играет важную роль в геометрии треугольников и отражает его внутреннюю гармонию и структуру. Понимание данной характеристики позволяет углубиться в изучение составляющих треугольника и использовать это знание для решения разнообразных геометрических задач.
Основные понятия и определения

В данном разделе мы рассмотрим основные термины и определения, связанные с явлением, о котором будет идти речь в данной статье. Мы будем говорить о центре окружности, находящейся внутри треугольника, и его свойствах, которые влияют на радиус вписанной окружности. Также мы рассмотрим понятие углов, определенных в треугольнике, и их взаимосвязь с радиусом вписанной окружности.
В таблице ниже приведены ключевые термины, которые будут использоваться в дальнейшем изложении:
| Термин | Определение |
|---|---|
| Центр окружности | Точка, находящаяся внутри окружности и равноудаленная от всех ее точек |
| Угол | Фигура, образованная двумя лучами с общим началом |
| Вписанный угол | Угол, вершина которого лежит на окружности, а стороны – нахождатся внутри нее |
| Остроугольный треугольник | Треугольник, у которого все углы меньше 90 градусов |
| Правильный треугольник | Треугольник, у которого все стороны и углы равны друг другу |
Знание этих основных понятий и определений позволит лучше понять и осмыслить специфику радиуса вписанной окружности в треугольнике и его связь с другими элементами этой фигуры.
Как определить мера вписанного контура?

Связь характеристик углов и сторон треугольника с центральной окружностью внутри него
Углы треугольника: Радиус вписанной окружности не только касается сторон треугольника, но и делит их пополам. Это означает, что каждая сторона треугольника будет являться хордой с радиусом вписанной окружности, а радиус будет являться перпендикуляром, опущенным из центра окружности на каждую из сторон. Величина углов треугольника также будет связана с радиусом вписанной окружности: углы, образованные хордами, будут пропорциональны радиусу окружности.
Стороны треугольника: Радиус вписанной окружности связан с длинами сторон треугольника через теорему тангенсов. Согласно этой теореме, квадрат радиуса окружности равен произведению длин отрезков, на которые стороны треугольника делят друг друга. Иными словами, сумма отношений радиуса вписанной окружности к длине каждой стороны треугольника равна 4, то есть r/a + r/b + r/c = 1/2, где r - радиус окружности, а a, b и c - длины сторон треугольника.
Площадь треугольника: Еще одна интересная связь - между радиусом вписанной окружности и площадью треугольника. Площадь треугольника можно выразить через радиус и полупериметр треугольника: S = pr, где S - площадь, p - полупериметр, r - радиус вписанной окружности. Это означает, что при увеличении радиуса вписанной окружности площадь треугольника также увеличивается.
Таким образом, радиус вписанной окружности оказывает глубокое влияние на характеристики треугольника, связывая углы, стороны и площадь треугольника вместе. Это делает его важной фигурой в геометрии и позволяет использовать его для решения различных задач и построений.
Итоговый размер центрального образования в треугольнике с неравными сторонами

С учетом различных размеров сторон треугольника, радиус вписанной окружности, также называемый размером центрального образования, приобретает определенные особенности.
Центральное образование, которое является естественной частью треугольника, может быть увеличено или уменьшено в зависимости от соотношений длин сторон. Интересно, что при неодинаковой величине сторон, радиус вписанной окружности может оказаться больше или меньше, чем в треугольниках со сторонами одинаковой длины.
Особенности радиуса центрального образования в разносторонних треугольниках могут быть объяснены взаимосвязью между углами и длинами сторон. Величина радиуса подвержена воздействию различного соотношения углов треугольника, а также пропорциональности точек вписанной окружности относительно сторон треугольника.
Таким образом, понимание особенностей радиуса центрального образования в треугольнике с неравными сторонами позволяет улучшить понимание геометрических свойств треугольников в целом.
Сущность внутренней окружности в треугольнике прямоугольной формы

Треугольник прямоугольной формы, который состоит из двух катетов и гипотенузы, характеризуется наличием особой внутренней окружности. Данное явление имеет свойство, подразумевающее нахождение радиуса окружности, необходимого для вписывания внутри треугольного контура.
Этот определенный радиус, оказывающийся относительно малым, определяет положение центра окружности внутри треугольника. Радиус вписанной окружности позволяет определить различные характеристики и особенности треугольника прямоугольной формы, такие как площадь, периметр и другие геометрические параметры.
Взаимосвязь между радиусом вписанной окружности и площадью треугольника
Существует интересная связь между радиусом вписанной окружности и площадью треугольника, которая позволяет нам лучше понять взаимодействие элементов геометрической фигуры. Радиус вписанной окружности отражает меру внутренней частности треугольника, а площадь треугольника измеряет степень его заполнения пространства. В этом разделе мы рассмотрим, как эти два понятия взаимодействуют между собой и какая связь между ними существует.
Одним из ключевых факторов взаимосвязи радиуса вписанной окружности и площади треугольника является теорема о площади треугольника, которая устанавливает, что площадь треугольника прямо пропорциональна радиусу вписанной окружности. С другими словами, чем больше радиус вписанной окружности, тем больше площадь треугольника, и наоборот.
Эта связь можно объяснить следующим образом: радиус вписанной окружности определяет глубину внутренней характеристики треугольника, в то время как площадь треугольника измеряет его заполненностьтерритории. Чем больше радиус вписанной окружности, тем дальше нужно проникнуть внутрь треугольника, чтобы заполнить достаточную для этого площадь. Следовательно, площадь треугольника будет больше.
Выражая эту взаимосвязь математически, можно сказать, что площадь треугольника S прямо пропорциональна квадрату радиуса вписанной окружности r: S = k * r^2, где k - постоянная пропорциональности. Это позволяет нам не только понять взаимосвязь между указанными характеристиками, но и вычислить площадь треугольника, если известен радиус вписанной окружности, и наоборот.
- Площадь треугольника прямо пропорциональна квадрату радиуса вписанной окружности.
- Чем больше радиус вписанной окружности, тем больше площадь треугольника.
- Математическое выражение этой связи: S = k * r^2, где S - площадь треугольника, k - постоянная пропорциональности, r - радиус вписанной окружности.
Познание взаимосвязи между радиусом вписанной окружности и площадью треугольника может помочь нам глубже понять и увидеть скрытые закономерности и свойства в геометрии. Это может быть полезным в решении различных задач и применении геометрических знаний в практических ситуациях.
Вопрос-ответ

Как определить радиус вписанной окружности в треугольнике?
Радиус вписанной окружности в треугольнике можно найти по формуле: $r = \frac{S}{p}$, где $S$ - площадь треугольника, а $p$ - полупериметр треугольника.
Какие особенности имеет радиус вписанной окружности в треугольнике равносторонней формы?
В равностороннем треугольнике радиус вписанной окружности равен одной трети длины стороны треугольника. Это свойство возникает из особенностей равностороннего треугольника, в котором все углы равны 60 градусов.
Какую роль играет радиус вписанной окружности в треугольнике?
Радиус вписанной окружности в треугольнике имеет большое значение при решении геометрических задач. Он позволяет находить площадь треугольника, длины сторон, углы между сторонами и другую информацию, связанную с треугольником.
В каких треугольниках радиус вписанной окружности будет максимальным?
Радиус вписанной окружности в треугольнике будет максимальным в случае, когда треугольник является равносторонним. В таком треугольнике все стороны равны, и, соответственно, радиус окружности будет наибольшим.
Как радиус вписанной окружности влияет на углы треугольника?
Радиус вписанной окружности влияет на углы треугольника следующим образом: если провести радиусы из центра окружности к точкам касания с сторонами треугольника, то эти радиусы будут являться угловыми биссектрисами треугольника.
Что такое радиус вписанной окружности в треугольнике?
Радиус вписанной окружности в треугольнике - это расстояние от центра окружности до любой стороны треугольника, которая касается этой окружности.



