Существует древняя наука, которая подобна энигме, где остроумие и интуиция скрываются за тонкими нитями логики. Она погружает нас в мир систем неравенств с одной неведомой, где каждый знак и коэффициент тайно встречаются в своих уравнениях и ограничениях.
Эта наука требует мастерства, предвидения и ловкости ума. Она обязывает нас мыслить нестандартно и видеть скрытые возможности, раскрывая всю мощь аналитического мышления. Загадками неравенств объединены силы алгебры и геометрии: одна стала фундаментом, а другая - путеводной нитью к ясности решения.
Для исследователей математического мира решение системы неравенств с одним неизвестным - это великое открытие истинной природы чисел. Это как раскрытие шифра, где каждый символ, каждое неравенство скрывает в себе собственные внутренние законы и особенности. И только тот, кто обладает уникальным зрением, сумеет проникнуть в их суть и найти уникальное решение. Вскрыть этот код можно только при помощи надежных инструментов и стратегического подхода.
Значимость решения системы неравенств с одним неизвестным в математических задачах
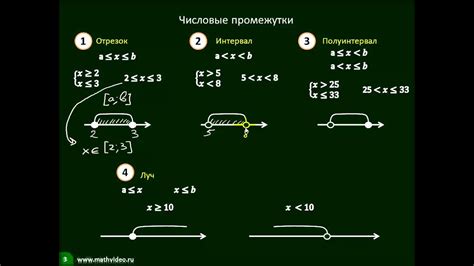
Существует одна важная математическая задача, связанная с нахождением решений систем неравенств с одним неизвестным. Возможность решения такой задачи имеет несомненную ценность в различных областях науки и применяется в реальной жизни. При изучении этой темы мы познакомимся с ее значениями и преимуществами, осознаем, как важно научиться справляться с такими задачами.
1. Позволяет моделировать реальные ситуации:
Умение решать системы неравенств с одним неизвестным позволяет абстрагировать и моделировать различные реальные ситуации. Многие проблемы, которые необходимо решить, связаны с неопределенностями и условиями, которые можно выразить в виде неравенств. Находя решение системы неравенств, мы сможем предсказать и оценить результаты исследуемой ситуации.
2. Используется для определения диапазона значений:
Решение систем неравенств позволяет определить возможный диапазон значений переменной. Это важно при решении задач, связанных с ограничениями. Например, при планировании бюджета, определении максимальных и минимальных температур или при анализе временных рамок для выполнения задачи.
3. Находит точку пересечения:
Решение таких систем неравенств может помочь определить точку пересечения графиков различных функций, что является ключевым понятием в алгебре. Это позволяет определить точку, в которой два кривых или линии пересекаются. Такой анализ полезен во многих областях, таких как экономика, инженерия и информационные технологии.
4. Решение оптимизационных задач:
Решение систем неравенств с одним неизвестным также играет важную роль при решении оптимизационных задач. Определение максимального или минимального значения функции при заданных условиях сводится к нахождению решения системы неравенств. Это применяется в экономике, производстве или в любой другой области, где требуется найти наилучший и наихудший сценарии.
Таким образом, решение систем неравенств с одним неизвестным - это важная математическая задача, которая находит свое применение во многих сферах. Отличное понимание и владение этой темой позволяет находить решения в неопределенных ситуациях, определять границы значений, находить точки пересечения графиков функций и решать задачи оптимизации.
Тайны эффективного разрешения группы неравенств

В данном разделе мы будем раскрывать секреты успешного решения системы неравенств с одним неизвестным. Здесь представлены интересные методы и инструменты, применение которых позволяет достичь оптимальных результатов при работе с неравенствами.
Самым важным фактором является правильное использование математических операций и свойств неравенств. Стройное и логичное применение арифметических операций, включая сложение, вычитание, умножение и деление, поможет упростить систему и найти искомое решение.
Важно также уметь распознавать ключевые слова и фразы в задачах с системами неравенств и понимать, как они отображаются в математических символах. Определения и интерпретации различных понятий с апелляцией к необходимым свойствам являются основой успешного решения неравенств.
Аккуратность и внимательность при работе с неравенствами также играют важную роль. Корректно записанная система и точный анализ ее частей помогут в идентификации ключевых паттернов и закономерностей, упрощающих процесс решения.
Краткость и лаконичность - еще один аспект эффективного решения систем неравенств. Умение сокращать записи и использовать упрощенные формы позволяет сэкономить время и упростить процесс решения.
В данном разделе мы рассмотрим и объясним различные стратегии и методы, которые помогут вам успешно и эффективно решать системы неравенств с одним неизвестным. Пошаговые примеры и конкретные практические советы помогут вам освоить все необходимые навыки и научиться достигать оптимальных результатов в решении математических задач.
Типы неравенств, часто встречающиеся в задачах

В математических задачах, связанных с решением системы неравенств с одним неизвестным, мы часто сталкиваемся с определенными типами неравенств. Понимание этих типов неравенств поможет нам эффективно подходить к решению задач и достичь успешных результатов.
Одним из наиболее часто встречающихся типов неравенств является линейное неравенство. В таких неравенствах неизвестная переменная входит только с линейным коэффициентом. Такие задачи обычно требуют нахождения диапазона значений, при которых выполняется неравенство.
Квадратичные неравенства также весьма распространены. В них неизвестная переменная входит в второй степени. Решение таких неравенств обычно требует использования методов факторизации и поиска корней, чтобы определить интервалы, в которых неравенство выполняется.
Условия с одними неравенством могут быть расширены до системы неравенств, где требуется одновременное выполнение нескольких неравенств. Встречающиеся типы систем неравенств могут быть как линейными, так и квадратичными.
- Неравенства с модулем - еще один важный тип задач. Здесь неизвестная переменная входит в модульный оператор, что требует рассмотрения двух случаев: когда модуль положителен и когда модуль отрицателен.
- Иррациональные неравенства - еще одна общая категория, требующая учета особенностей иррациональных чисел и знание методов их решения.
- Экспоненциальные и логарифмические неравенства - этот тип задач связан с нахождением значений переменной в подзаданных интервалах в рамках экспоненциальных и логарифмических функций.
Понимание разных типов неравенств и их решений является важным компонентом успешного решения систем неравенств с одним неизвестным. Каждый тип неравенства имеет свои особенности и требует определенных методов для достижения корректных ответов.
Важные этапы построения решения

Следующие шаги представляют собой неотъемлемые компоненты процесса нахождения ответа на систему неравенств с одним неизвестным, в котором кроются основные принципы эффективной работы с математическими задачами. Понимание и освоение этих этапов не только разовьет навыки логического мышления, но также поможет справиться с трудными задачами и достичь желаемого результата.
Анализ задачи: В этом шаге необходимо внимательно изучить условие, разобрав его на составные части и выделить ключевую информацию. Важно понять, что требуется найти и какие ограничения имеются.
Построение математической модели: На этом этапе мы переводим условие задачи в язык математики, используя переменные и неравенства. Математическая модель должна отражать все ограничения из условия.
Решение модели: В этом шаге мы применяем математические методы, чтобы получить точное или приближенное решение модели. Мы можем использовать различные техники, такие как графическое представление, алгебраические методы или численные методы.
Проверка и интерпретация: После нахождения решения мы должны проверить его, подставив его обратно в исходную систему неравенств. Также важно интерпретировать полученный ответ в контексте задачи.
Эти этапы являются фундаментом для эффективного решения системы неравенств с одним неизвестным. Они позволяют разбить сложную задачу на более простые составляющие, поэтому необходимо уделить им должное внимание и тщательно продумать каждый шаг.
Завязка задачи: разбор примеров

В данном разделе мы рассмотрим несколько примеров задач, связанных с решением системы неравенств с одним неизвестным. Мы проанализируем различные сценарии и подходы к их решению, чтобы лучше понять суть и методы работы с такими задачами.
Взглянем на первый пример. Предположим, у нас есть система неравенств с одной переменной, которая описывает диапазон возможных значений этой переменной. Наша задача состоит в определении интервала или отрезка, в котором находятся все допустимые значения переменной, удовлетворяющие условиям системы.
Далее рассмотрим другой пример. Представим, что у нас есть система неравенств, где помимо переменной, встречаются также константы и выражения с другими переменными. В этом случае задача заключается в определении диапазона, в котором может находиться значение одной переменной при условии, что все остальные переменные принадлежат определенному интервалу значений.
Также рассмотрим ситуацию, когда система неравенств имеет дробные коэффициенты или знаки неравенства отличаются от обычных "". В таких задачах наша задача состоит в определении интервала значений переменной, удовлетворяющих данной системе неравенств.
Разбор данных примеров позволит нам лучше понять разнообразие ситуаций, с которыми мы можем столкнуться при решении систем неравенств с одной неизвестной. Наблюдение за различными случаями поможет нам уловить общие шаблоны и подходы к решению таких задач, что, в свою очередь, позволит нам легче справиться с будущими математическими задачами.
Опасные штрихи в пути к решению системы неравенств
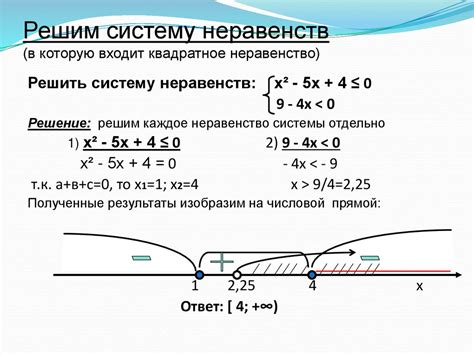
Возможны различные сложности и подводные камни при решении системы неравенств, которые могут затруднить или неправильно упростить процесс. В данном разделе мы рассмотрим некоторые из них, чтобы дать вам ясное представление и избежать ошибок.
- Неправильное понимание условий и ограничений: основной камень преткновения при решении системы неравенств - это неверное или неполное понимание условий задачи. Необходимо внимательно читать и анализировать условия, чтобы точно определить, какие неравенства нужно использовать и какие они должны быть знаки.
- Игнорирование исключений и особых случаев: некоторые задачи могут иметь исключения или особые случаи, которые необходимо учесть. Не следует игнорировать такие особенности, так как это может привести к неправильному решению.
- Неправильная обработка логических операций: при решении системы неравенств часто приходится использовать логические операции типа "или" или "и". Неправильная обработка таких операций может привести к некорректному решению задачи.
- Неправильные шаги при упрощении: одна из ключевых фаз решения системы неравенств - это упрощение выражений путем применения математических операций. Ошибки при упрощении могут сместить результат и привести к неправильному ответу.
- Пропуск проверки решения: после получения ответа на систему неравенств необходимо провести финальную проверку, чтобы убедиться в его правильности. Многие ошибки возникают из-за невнимательности и непроверки окончательного решения.
Важно иметь в виду эти подводные камни и быть внимательным при решении системы неравенств, чтобы достичь успешного и точного результата. Не торопитесь и проверяйте каждый шаг, чтобы избежать возможных ошибок.
Как преодолеть трудности при преобразовании неравенств?

В этом разделе мы рассмотрим некоторые полезные подходы и стратегии, которые помогут вам преодолеть трудности при преобразовании неравенств. Нами будут исследованы техники, позволяющие точно и эффективно работать с неравенствами и достичь желаемого результата.
Первым шагом в преодолении трудностей является построение плана действий. Вам необходимо проанализировать данное неравенство, выделить основные компоненты и определить возможные стратегии трансформации. Затем стоит разработать последовательность шагов, которая поможет вам достичь конечного решения.
Далее, при работе с неравенствами, очень важно правильно применять свойства неравенств. Например, если в задаче присутствует сложение или вычитание, вам может потребоваться изменить знак неравенства. Если есть деление на отрицательное число, вам придется поменять направление неравенства. Правильное применение этих свойств позволит вам упростить неравенство и привести его к более удобному виду для дальнейших преобразований.
Кроме того, важно учитывать особенности различных типов неравенств. Например, при решении квадратных неравенств может понадобиться использовать факторизацию или определение знака выражения внутри квадратного корня. Необходимо быть внимательным и аккуратным при работе с каждым конкретным типом неравенств, чтобы не допустить ошибок.
Однако, очень важно не только знать и применять техники преобразования неравенств, но и учитывать допустимые промежутки значений переменных. Некоторые операции могут приводить к изменению диапазона значений переменных, и вам необходимо следить за этим, чтобы не потерять возможные решения или не получить некорректное окончательное решение.
Секреты эффективной работы с неравенствами

Изысканное искусство математического мышления стремится к покорению самых сложных задач нахождения решений. Неравенства, со своей капризной природой, требуют особого подхода и глубокого понимания. В этом разделе мы рассмотрим важные секреты успешной работы с неравенствами, которые помогут вам с легкостью преодолеть каждое ограничение и найти желанное решение.
1. Определите направление: Неравенства могут ограничивать область возможных значений переменной, указывая либо на множество положительных значений, либо на множество отрицательных. Важно указать правильное направление, чтобы не потерять возможные решения. Анализируйте знаки и свойства неравенств, чтобы определить правильное направление своих расчетов.
2. Используйте алгебраические преобразования: Так же, как в уравнениях, можно применять алгебраические преобразования для упрощения неравенств. Добавление или вычитание одного и того же числа к обеим сторонам, умножение или деление на положительное число - все эти операции сохраняют знак неравенства. Однако, при умножении или делении на отрицательное число, необходимо поменять знак неравенства.
3. Будьте внимательны к исключениям: Некоторые операции могут вносить исключения в решение неравенства. Например, при умножении или делении на переменную, нужно учитывать ее возможное значение нуля и получить допустимые диапазоны решений. Анализируйте возможные исключения и учитывайте их в ходе работы с неравенствами.
4. Применяйте графическое представление: Построение графика неравенства может помочь наглядно представить его решение и определить важные точки пересечения графиков. Используйте графический метод вместе с алгебраическими приемами, чтобы увидеть полную картину и легче найти решение.
5. Продолжайте итерацию: Возможно, вам придется провести несколько итераций и использовать различные методы для решения сложных систем неравенств. Будьте гибкими и терпеливыми, и ваш порыв к решению будет вознагражден.
Понимание этих секретов позволит вам мастерски работать с неравенствами и открывать особенности их решений. Доверьтесь своим математическим навыкам и откройте для себя вселенную возможностей, которую предоставляют неравенства.
Важность внимательного анализа условий и ограничений

Тщательное понимание условий задачи и ограничений помогает определить границы, в которых необходимо искать возможное решение. Анализируя эти ограничения, можно выделить ключевые отрезки числовой прямой, на которых искомая величина может принимать значения. Это позволяет сузить область поиска и сфокусироваться на наиболее перспективных вариантах.
Кроме того, внимательное восприятие условий задачи дает возможность обнаружить дополнительные свойства и ограничения, которые могут быть полезны при решении. Это может включать в себя информацию о знаке неизвестной величины, диапазонах, в которые она может попадать, или дополнительных соотношениях между неизвестными. Анализ этих дополнительных условий упрощает постановку и решение системы неравенств, а также может привести к появлению новых подходов и стратегий.
В конечном счете, внимательный анализ условий и ограничений является неотъемлемым элементом успешного решения математических задач. Это позволяет определить границы поиска, выделить ключевые отрезки и свойства, а также использовать дополнительные соотношения между переменными. Благодаря этому, математические задачи становятся более доступными и интересными для решения, открывая возможность для креативного подхода и открытия новых решений.
Применение различных подходов к поиску и анализу результатов

Метод графиков - один из наиболее популярных подходов к решению систем неравенств. Этот метод основан на построении графиков всех неравенств и анализе пересечений графиков. Позволяет наглядно представить решение системы и удобен при работе с небольшим количеством неравенств.
Алгебраический метод - подход, основанный на алгебраическом преобразовании системы неравенств с целью упрощения и анализа. В данном методе используются правила и свойства алгебры, чтобы привести систему к более простому виду и получить решение. Часто используется для систем с большим количеством неравенств.
Интуитивный метод - подход, основанный на интуитивном понимании и оценке результатов системы неравенств. В этом случае математик может использовать свои знания и опыт для оценки значений неизвестных и получения примерного решения. Этот метод может быть полезен, когда точные математические методы не дают однозначного результата или приближенного значения.
Каждый из описанных подходов имеет свои преимущества и ограничения, поэтому выбор метода зависит от сложности системы неравенств и требуемой точности результатов. Иногда лучшим решением может быть комбинация нескольких подходов, чтобы достичь наилучших результатов.
Вопрос-ответ

Что такое система неравенств с одним неизвестным?
Система неравенств с одним неизвестным - это набор математических выражений, содержащих неравенства и одну переменную. Задача состоит в нахождении всех значений этой переменной, при которых все неравенства выполняются одновременно.
Как можно решить систему неравенств с одним неизвестным?
Для решения системы неравенств с одним неизвестным необходимо выполнить несколько шагов. Сначала объедините все неравенства вместе, затем упростите выражение и избавьтесь от скобок. Далее решите получившееся уравнение, найдите границы изменения переменной и проверьте их на валидность. Найденные значения будут являться решениями системы.
Какие секреты успешного решения математической задачи связаны с решением системы неравенств с одним неизвестным?
Одним из секретов успешного решения системы неравенств с одним неизвестным является тщательное и систематичное выполнение всех шагов алгоритма решения. Важно не упускать никаких деталей и следовать строго определенному порядку действий. Также важно быть внимательным и аккуратным при работе с математическими выражениями, чтобы избежать ошибок в процессе решения задачи.



