В этой статье мы предлагаем подробное пошаговое руководство, которое позволит вам разобраться с основами алгебры для 7 класса с использованием учебника Макарычева номер 904. Здесь мы не только предоставим вам информацию об учебнике и его особенностях, но и подробно разберем, как правильно выполнить все задания и упражнения, представленные в нем.
Ваше путешествие в мир алгебры начнется с изучения базовых понятий и основных принципов этой науки. С помощью учебника Макарычева номер 904 вы сможете освоить такие понятия, как переменные, коэффициенты, многочлены и многое другое. Наше руководство позволит вам разобраться в каждом из этих понятий, а также дать вам навыки для успешного применения их в практических заданиях.
Одним из ключевых аспектов успешного изучения алгебры является понимание основных правил и принципов, которые касаются операций с числами и переменными. В нашем руководстве мы акцентируем внимание на важности строгого следования этим правилам. Мы подчеркиваем необходимость внимательного и точного выполнения каждого действия, чтобы избежать ошибок и снять различные сомнения, которые могут возникнуть в процессе решения задач.
Тема: Разбор задачи по алгебре для 7 класса по учебнику Макарычева

В данном разделе мы рассмотрим задачу по алгебре из учебника Макарычева для 7 класса. В этой задаче мы применим различные алгебраические понятия и методы для решения конкретных проблем, используя разнообразные операции и формулы. В ходе выполнения задания мы разберем шаги решения, объясним их логику и дадим подробное обоснование каждого этапа.
| Ключевые термины | Синонимы |
|---|---|
| Задача | Упражнение |
| Учебник | Пособие |
| Алгебра | Вычислительная математика |
| Алгебраические понятия | Арифметические концепции |
| Методы | Способы |
| Операции | Действия |
| Формулы | Уравнения |
| Решение | Выполнение |
| Обоснование | Объяснение |
| Логика | Мыслительные процессы |
Основные понятия алгебры в седьмом классе

Переменные – это символы, которые представляют неизвестные значения в алгебраических выражениях и уравнениях. Они помогают нам решать задачи и находить нужные значения.
Коэффициенты – это числа, стоящие перед переменными. Они определяют, сколько раз переменная входит в данное выражение. Коэффициенты могут быть положительными, отрицательными или нулевыми.
Термы – это части алгебраических выражений, разделенные знаками сложения или вычитания. Они могут состоять из одного или нескольких слагаемых. Термы могут быть простыми или сложными, в зависимости от количества переменных и арифметических операций.
Многочлены – это алгебраические выражения, состоящие из нескольких термов, соединенных знаками сложения или вычитания. Многочлены могут иметь разные степени, высчитываемые по наибольшей степени переменной.
Изучение основных понятий алгебры в 7 классе позволит вам лучше понимать математические задачи и решать их с помощью алгебраических методов. Это полезные навыки, которые пригодятся вам как в школе, так и в жизни.
Правила работы с алгебраическими выражениями в задаче № 904

В данном разделе будут представлены основные принципы и правила работы с алгебраическими выражениями в задаче номер 904. Будут рассмотрены способы упрощения, раскрытия скобок, приведения подобных членов и другие алгебраические манипуляции, необходимые для решения данной задачи.
Упрощение выражения
Первым шагом является упрощение алгебраического выражения путем сокращения подобных членов. Для этого необходимо сложить или вычесть между собой те части выражения, которые имеют одинаковые переменные и степени. Также следует производить сокращение подобных слагаемых внутри скобок.
Раскрытие скобок
После упрощения выражения следует приступить к раскрытию скобок. Это означает умножение каждого члена внутри скобок на число, стоящее перед скобкой. При раскрытии скобок необходимо учесть знаки перед скобками: если перед скобкой стоит плюс, то знаки внутри скобок сохраняются, а если перед скобкой стоит минус, то знаки внутри скобок меняются на противоположные.
Приведение подобных членов
После раскрытия скобок следует приведение подобных членов. Подобные слагаемые - это те, у которых одинаковые переменные и степени. Для приведения подобных членов слагаемые складываются или вычитаются.
Другие алгебраические манипуляции
Помимо упрощения, раскрытия скобок и приведения подобных членов, решение задачи номер 904 может также включать другие алгебраические манипуляции, такие как домножение на общий множитель, факторизация и нахождение обратного выражения.
Понимание и применение этих правил поможет вам успешно решить задачу номер 904, а также развить навыки работы с алгебраическими выражениями в целом.
Алгоритм решения уравнений в 7 классе: последовательность действий

Раздел предлагает алгоритмическое руководство по решению уравнений в 7 классе. Здесь представлена последовательность действий, которые помогут ученикам успешно справиться с этой задачей. Для решения уравнений необходимо следовать определенным этапам, а именно: определение типа уравнения, приведение его к стандартному виду, исполнение соответствующих действий с переменными и выявление корректного ответа. В процессе выполнения упражнений ученикам будет предложено решить разнообразные уравнения, применяя полученные знания в практике. Усвоение этого алгоритма позволит ученикам стать уверенными в решении уравнений и преодолеть возможные трудности.
Методы решения задач на соотношения в алгебре
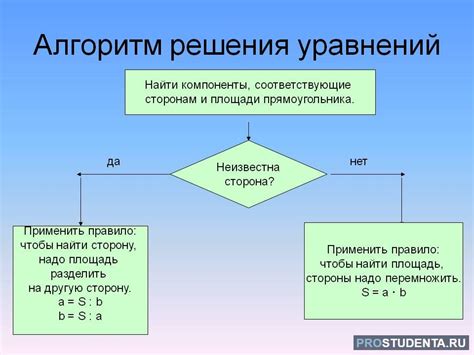
Первый метод - это метод пропорции. Он заключается в установлении равенства двух отношений, где известные значения соответствуют друг другу пропорционально неизвестным, а неизвестные значения – также пропорциональны друг другу. С помощью этого метода можно решать задачи на пропорциональное деление и умножение, а также на сравнение двух величин.
Второй метод – это метод использования пропорциональной картинки. Он основан на построении графической модели, где каждый элемент представлен в виде определенного количества единиц. Задачи на пропорциональность решаются путем сравнения и анализа пропорциональных отношений, изображенных на картинке.
Третий метод – это метод использования формул и уравнений. Он заключается в применении известных формул и уравнений для решения задач на пропорциональность. С помощью этого метода можно решать задачи на пропорциональное увеличение и уменьшение, а также на решение уравнений с пропорциональными отношениями.
В данном разделе мы рассмотрим каждый из этих методов более подробно, а также предоставим примеры задач, которые можно решить с их помощью. Познакомившись с этими методами, вы сможете легко и точно решать задачи на пропорциональность в алгебре.
Использование математических выражений в задаче под номером 904

В данном разделе мы рассмотрим применение законов алгебры для решения задачи номер 904 из учебника "Алгебра, 7 класс" автора Макарычева. В этой задаче будет использован набор математических формул, которые позволят нам постепенно разобрать и решить ее.
Математические формулы позволяют нам описывать и решать конкретные задачи, используя символы и операции, эффективно выражая идеи и отношения между различными величинами. В задаче номер 904 мы будем применять формулы для нахождения значений неизвестных и решения уравнений.
- Первым шагом будет анализ задачи и выделение из нее ключевых понятий, которые позволят сформулировать математические уравнения. С помощью формул мы сможем выразить величины, связанные с задачей, через неизвестные значения.
- Затем перейдем к составлению уравнений, используя известные нам формулы и выражения. Это позволит нам свести задачу к математической модели и сформулировать конкретные уравнения.
- После составления уравнений перейдем к их решению. В этом этапе мы будем использовать различные алгебраические приемы и методы для нахождения значений неизвестных и полной вертикальной прямой, описывающей график функции.
Использование математических выражений и формул в задаче номер 904 поможет нам разобраться в ее сути и предоставит нам возможность получить точный и надежный результат. Это необходимо для эффективного решения алгебраических задач и развития навыков работы с математическими выражениями.
Роль коэффициента в алгебре: ключевой элемент для решения уравнений и построения графиков

В алгебре коэффициенты играют важную роль в решении уравнений и построении графиков. Коэффициенты определяют, как различные переменные зависят друг от друга, влияют на изменение значений и формулы в математических выражениях. Изучение концепции коэффициента помогает понять и применять алгебраические методы для анализа и решения широкого спектра проблем, от простых до сложных.
Примеры коэффициентов
Коэффициенты могут представлять собой числа, факторы, буквенные обозначения или их комбинации. Например, в уравнении 3x + 2y = 7 коэффициенты 3 и 2 указывают на то, как изменяются значения переменных x и y при решении уравнения. В выражении 2x^2 + 5x - 3 коэффициенты 2, 5 и -3 определяют связь между степенями переменной x.
Решение уравнений с помощью коэффициентов
Зная значения коэффициентов, мы можем использовать алгебраические методы для нахождения неизвестных переменных и решения уравнений. Например, при решении квадратного уравнения ax^2 + bx + c = 0 коэффициенты a, b и c позволяют нам применить формулу дискриминанта и найти корни уравнения. Вычисление и анализ значений коэффициентов помогает нам понять, как уравнение связано с графиком функции и найти точки пересечения с осями координат.
Значимость коэффициентов в алгебре
Коэффициенты играют роль не только в решении уравнений, но и в построении графиков функций и анализе их свойств. Изучая и учитывая значения коэффициентов, мы можем определить симметрию графика, наличие экстремумов, характер поведения функции и ее асимптоты. Таким образом, знание и понимание коэффициентов позволяют нам более глубоко и точно анализировать и работать с алгебраическими выражениями и уравнениями.
Графическое решение уравнений и неравенств в задаче номер 904
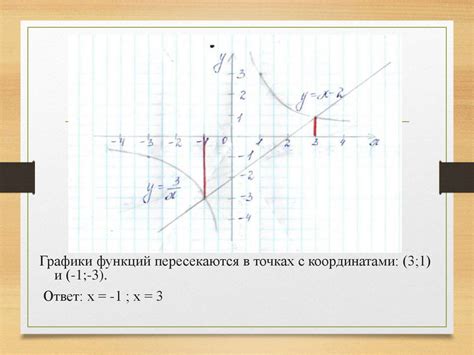
В данном разделе представлен подход, основанный на визуальном представлении и графическом решении уравнений и неравенств в контексте задачи номер 904 учебника алгебры для 7 класса Макарычева. Используя графический метод, мы можем наглядно представить различные решения и интерпретировать их геометрически. Это позволяет учащимся лучше понять и визуализировать математические концепции, а также расширить свои навыки в решении задач.
| Шаги графического решения |
|---|
| 1. Представьте уравнение или неравенство в виде функции или выражения, содержащего переменную. |
| 2. Постройте координатную плоскость и отметьте оси. |
| 3. Запишите уравнение или неравенство в форме y = f(x). |
| 4. Представьте график этой функции на координатной плоскости. |
| 5. Найдите точки пересечения графика с осями координат или другими графиками, если это необходимо. |
| 6. Проанализируйте график, чтобы определить решение уравнения или неравенства. |
Графическое решение уравнений и неравенств позволяет наглядно исследовать и находить решения поставленных задач. Оно может быть полезным при работе с сложными уравнениями и неравенствами, а также позволяет проверять правильность полученных ответов. При использовании этого метода важно помнить о его ограничениях и уметь интерпретировать полученные результаты в контексте задачи. Графическое решение является одним из инструментов, которые помогут студенту лучше визуализировать и понять математические концепции.
Техника работы с системами уравнений в алгебре

Для успешного решения систем уравнений необходимо понимание основных понятий, таких как переменная, уравнение, система уравнений, коэффициенты и т.д. При работе с системами уравнений часто используются методы замены, сложения и вычитания уравнений, а также приведения системы к более удобному виду.
Одним из ключевых понятий при работе с системами уравнений является равносильность. Равносильные системы - это такие системы уравнений, которые имеют одинаковое множество решений. Для определения равносильных систем применяются различные преобразования, такие как умножение уравнений на число или их суммирование и вычитание.
Для наглядного представления и анализа систем уравнений, часто используется таблица. В таблице помещаются все уравнения системы, а значения переменных записываются в соответствующие ячейки. Такой подход упрощает выявление зависимостей между переменными и нахождение решений системы. При необходимости, в таблице можно использовать дополнительные столбцы для промежуточных вычислений или учета введенных условий.
Для успешной работы с системами уравнений рекомендуется усваивать базовые методы решения и тренироваться на практических задачах. В дальнейшем, эти навыки позволят не только успешно решать системы уравнений, но и применять их в реальных жизненных ситуациях, где нужно найти несколько неизвестных величин, удовлетворяющих определенным условиям.
| Принципы работы с системами уравнений: | Примеры методов решения: |
|---|---|
| Определение понятий и терминов | Метод замены |
| Равносильность систем уравнений | Метод сложения и вычитания |
| Использование таблицы для анализа системы уравнений | Метод приведения к более удобному виду |
Решение задач по поиску неизвестного значения в алгебре поэтапно

Этот раздел представляет подробное руководство, которое позволит вам научиться решать задачи алгебры класса 7 по поиску неизвестного значения. Здесь приведены шаги, используемые при решении таких задач, и приведены примеры для наглядности.
Для начала, мы разберем принципы решения задач на нахождение неизвестного значения. Учебный материал объяснит вам, как проводить необходимые математические операции, что позволит вам точно определить неизвестное значение в алгебре.
Затем мы перейдем к конкретным примерам, в которых будут поставлены задачи на поиск неизвестного значения. Каждый пример будет детально разобран, шаг за шагом, с объяснением каждого этапа решения.
В этом разделе также будет использоваться таблица, чтобы обеспечить более наглядное представление процесса решения. Таблица будет показывать значения переменных на каждом шаге решения и промежуточные результаты, чтобы вы могли следовать за каждым шагом и легко воспроизводить решение задач самостоятельно.
После изучения этого раздела вы сможете успешно решать задачи, связанные с поиском неизвестного значения в алгебре, и будете уверены в своих навыках решения таких задач.
| Шаг | Описание |
|---|---|
| 1 | Определение переменных и условий задачи |
| 2 | Формулировка уравнения на основе заданных условий |
| 3 | Преобразование уравнения с целью изолирования неизвестного значения |
| 4 | Решение полученного уравнения для определения неизвестного значения |
| 5 | Проверка полученного решения и его интерпретация в контексте задачи |
Практические рекомендации для решения задачи алгебры

Этот раздел предлагает полезные советы и подсказки для успешного решения задачи данного учебника по алгебре. Вам будет представлена методика, которая поможет вам лучше понять условие задачи, определить ключевые данные и правильным образом применить соответствующие алгебраические операции.
1. Внимательно прочитайте условие задачи: Прежде чем начинать решать задачу, важно внимательно прочитать условие и понять его содержание. Обратите особое внимание на имена, числа и ключевые слова, которые могут указывать на необходимые операции или алгоритмы решения.
2. Разберите условие на ключевые элементы: После чтения задачи, разберите ее на отдельные ключевые элементы - данные, вопрос и известные ограничения. Это поможет вам лучше ориентироваться в задаче и определить необходимые действия.
3. Используйте алгебраические методы для решения: В зависимости от типа задачи, определите, какие алгебраические методы или формулы могут быть применены для ее решения. Не забывайте использовать правила математических операций и алгебраические свойства, чтобы получить окончательный результат.
4. Проверьте правильность решения: После получения ответа, проведите проверку его правильности. Убедитесь, что ваше решение соответствует условию задачи и логически верно.
Следуя этим практическим советам, вы сможете эффективно и точно решать задачи по алгебре и достигать успеха в обучении.
Вопрос-ответ

Какие темы из алгебры рассматриваются в упражнении номер 904 учебника Макарычев для 7 класса?
В упражнении номер 904 учебника Макарычев для 7 класса рассматривается тема "Решение уравнений".
Какова структура решения уравнений в упражнении номер 904 учебника Макарычев для 7 класса?
Структура решения уравнений в упражнении номер 904 учебника Макарычев для 7 класса состоит из следующих шагов: запись уравнения, определение типа уравнения (линейное, квадратное и т.д.), приведение уравнения к стандартному виду, решение уравнения, проверка полученного решения.
Какие методы применяются для решения уравнений в упражнении номер 904 учебника Макарычев для 7 класса?
В упражнении номер 904 учебника Макарычев для 7 класса для решения уравнений применяются различные методы, в зависимости от типа уравнения: метод подстановки, метод равенства исходного уравнения нулю, метод графического изображения и т.д.
Какие трудности могут возникнуть при решении уравнений в упражнении номер 904 учебника Макарычев для 7 класса?
При решении уравнений в упражнении номер 904 учебника Макарычев для 7 класса могут возникнуть следующие трудности: недостаточные знания базовых математических операций, неумение приводить уравнения к стандартному виду, ошибки при вычислениях, неумение проверять полученные решения на соответствие исходному уравнению.
Какие примеры задач можно решить с помощью упражнения номер 904 учебника Макарычев для 7 класса?
С помощью упражнения номер 904 учебника Макарычев для 7 класса можно решить различные задачи, связанные с решением уравнений, например: задачи на нахождение неизвестных величин при известных условиях, задачи на нахождение корней уравнений, задачи на проверку правильности решения уравнения и т.д.
Как можно решить задачу номер 904 из алгебры 7 класса Макарычев?
Для решения задачи номер 904 из алгебры 7 класса Макарычев необходимо следовать определенным шагам. Первоначально, ознакомьтесь с условием задачи и выделите главные величины. Затем, используя изученные в теории методы и формулы, произведите необходимые вычисления. После этого, проанализируйте полученный ответ и проверьте его на соответствие заданию. В случае необходимости, примените дополнительные методы решения или проверки ответа. В конце, оформите решение задачи в понятной и логичной форме.
Какие основные темы и концепции рассматриваются в алгебре 7 класса Макарычев?
В алгебре 7 класса Макарычев основные темы включают в себя: числа и их свойства, алгебраические выражения и их упрощение, уравнения и неравенства, работа с графиками прямых линий и так далее. Концепции, изучаемые в этом курсе, включают в себя: операции с числами (сложение, вычитание, умножение, деление), использование алгоритмов и методов решения уравнений и неравенств, понимание графиков и их анализ. Учебник Макарычева предоставляет подробные объяснения и многочисленные примеры для более глубокого понимания этих тем и концепций.