В мире цифровой логики существует непрерывная потребность в переводе логических условий на понятный для компьютера язык математических символов. Одним из наиболее эффективных инструментов является использование карт Карно и метода квайновой нормальной формы (КНФ). С помощью этой техники можно легко и точно представить сложные логические функции, сделав их более доступными для понимания и дальнейшей обработки.
Однако, создание КНФ по карте Карно требует тщательного анализа и технического мастерства. Начинающим может показаться сложным сам процесс перевода, а кажется, что погрузиться в мир символов и математических операций – отнюдь не легкая задача. Но не стоит пугаться! Мы предлагаем подробное руководство, которое поможет вам разобраться с этим проблемным вопросом и научиться создавать КНФ по карте Карно без лишних сложностей.
Зачем, спросите вы, нам вообще создавать КНФ по карте Карно? Ответ прост: это необходимо для более эффективного решения задачи, связанной с обработкой логических условий. Да, можно обойтись и без этого инструмента, но только зачем усложнять себе жизнь и потерять много времени на поиски оптимального решения? С помощью карты Карно и метода КНФ вы сможете систематизировать информацию, упростить логическое выражение и ускорить выполнение задачи в несколько раз. Это как сокращение пути от А до Б, только в мире логики и программирования.
Основные понятия: карта Карно и Конъюнктивная нормальная форма

В этом разделе мы погрузимся в основные понятия, выделенные в теме: "Как сделать КНФ по карте Карно: подробное руководство." Рассмотрим, что представляет собой карта Карно и как она связана с конъюнктивной нормальной формой (КНФ).
Карта Карно – это графический инструмент, используемый для анализа логических выражений и упрощения логических функций. С помощью карты Карно можно наглядно представить взаимосвязь между различными комбинациями переменных и значениями функции, которую они определяют. Карта Карно помогает обнаружить закономерности и преобразовать логическое выражение в более простую форму.
Конъюнктивная нормальная форма (КНФ) является одной из формальных систем представления логических функций. Она представляет собой дизъюнкцию конъюнкций литералов, где каждая конъюнкция соответствует одному истинному значению функции. Преобразование логической функции в КНФ может быть полезным для анализа и оптимизации работы цифровых схем. КНФ также позволяет удобно работать с картой Карно и упрощать логические выражения.
Определение и основные концепции

Карта Карно - это графическое представление логической функции, в котором все возможные комбинации входных значений упорядочены и расположены на двумерном прямоугольнике. Карта Карно позволяет визуализировать зависимость между входными переменными и выходными значениями.
Конъюнкция - это булева операция, которая соответствует логическому умножению и представляет собой логическое "И" между двумя или более переменными. В результате конъюнкции значение будет истинным только в том случае, если все переменные являются истинными.
Дизъюнкция - это булева операция, которая соответствует логическому сложению и представляет собой логическое "ИЛИ" между двумя или более переменными. В результате дизъюнкции значение будет истинным, если хотя бы одна из переменных является истинной.
Логическая функция - это математическое выражение, которое описывает зависимость между входными переменными и выходными значениями. Логическая функция может быть выражена с помощью различных операций, таких как конъюнкция, дизъюнкция, отрицание и других.
Конъюнктивная нормальная форма (КНФ) - это один из способов представления логической функции, в котором она выражается как конъюнкция дизъюнкций. КНФ позволяет представить логическую функцию в виде совокупности элементарных конъюнкций, каждая из которых соответствует одному выходному значению.
В следующих разделах статьи более подробно будет рассмотрено применение этих понятий при создании КНФ по карте Карно и представлена пошаговая инструкция по этому процессу.
Преимущества применения анализа картой Карно

1. Удобство визуализации и понимания: Карта Карно представляет собой графическую схему, где каждая ячейка соответствует конкретному набору входных переменных. Такая визуальная форма позволяет легко представить связь между входными значениями и соответствующими выходными результатами, что значительно упрощает анализ и понимание функции.
2. Минимизация количества литералов: Используя карту Карно, можно произвести минимизацию логической функции путем группировки ее смежных ячеек. Такой подход позволяет сократить количество переменных и уравнений в полученной конъюнктивной нормальной форме (КНФ), что упрощает последующую обработку и реализацию логических схем.
3. Обнаружение ошибок и неисправностей: При анализе больших и сложных функций с помощью карты Карно легко обнаружить ошибки в логической схеме или некорректное задание функции. Визуальное представление функции позволяет быстро выявить неправильные или неполные группировки ячеек, а также пропущенные сочетания входных переменных.
4. Улучшение производительности и эффективности: Применение карты Карно позволяет оптимизировать логические функции и минимизировать суммарное количество операций, необходимых для их выполнения. Это позволяет достичь значительного улучшения производительности логических схем и снижения энергопотребления при их реализации в аппаратных устройствах.
Почему стоит выбрать данный подход

В условиях современного мира, где важно стремиться к оптимальности и эффективности, выбор подходящего метода для создания точной нормальной формы (КНФ) по карте Карно может оказаться решающим фактором. Несмотря на разнообразие доступных инструментов, данный метод представляет собой непременный инструмент, обеспечивающий точность и надежность в процессе анализа и оптимизации логических функций.
Интуитивная идея использования карты Карно в создании КНФ позволяет легко визуализировать и анализировать булевы функции. Вместо того чтобы работать непосредственно с абстрактными символами, можно использовать графическое представление, что значительно упрощает процесс понимания логической структуры функций и возможных оптимизаций.
Достоинством данного подхода является его гибкость. По карте Карно можно анализировать и оптимизировать функции различных размеров и сложностей. Независимо от количества входных переменных, метод всегда остается применимым и позволяет учесть все возможные комбинации значений переменных, что гарантирует получение точной нормальной формы.
Важно отметить, что использование карты Карно в создании КНФ позволяет значительно сократить время и усилия, затрачиваемые на анализ и оптимизацию логических функций. Благодаря интуитивному и гибкому подходу, инженеры и специалисты могут сфокусироваться на сущности проблемы, а не тратить время на осознание и анализ сложных абстрактных кодов.
Подготовка данных для создания схемы Карно
Первым шагом в подготовке данных является анализ исходной булевой функции, определение ее переменных и их возможных значений. Необходимо изучить логику функции и выделить все возможные комбинации значений переменных. Это поможет нам построить таблицу истинности для функции.
Далее мы можем перейти к построению таблицы истинности. Для каждой комбинации значений переменных функции определяем соответствующее значение выражения. Таким образом, мы получим таблицу, где каждая строка представляет собой одну из комбинаций значений переменных, а последняя колонка – соответствующие значения функции.
Однако, часто булевые функции имеют большое количество переменных, и построение полной таблицы истинности может быть сложной задачей. В таком случае, мы можем использовать методы упрощения функций, такие как алгоритмы Квайна-МакКласки, чтобы минимизировать количество строк в таблице истинности и упростить дальнейшую работу с схемой Карно.
После подготовки данных и упрощения функции мы готовы приступить к построению карты Карно. Эта карта представляет собой таблицу, разделенную на ячейки, где каждая ячейка соответствует одной комбинации значений переменных. В каждой ячейке мы указываем соответствующее значение функции.
Теперь, когда мы подготовили все необходимые данные, мы можем приступить к последующим шагам создания схемы Карно. В следующем разделе мы рассмотрим, как заполнить и анализировать карту Карно для получения упрощенной логической функции.
Корректное описание входных данных
При работе с картой Карно необходимо предоставить точное и четкое описание исходных данных. В этом разделе мы объясним, каким образом правильно описать информацию, которая будет использоваться для создания КНФ.
Для начала, нужно передать информацию о величинах и свойствах переменных вашего логического выражения. Здесь важно быть ясным и точным, чтобы исключить возможные неоднозначности. Необходимо указать символы или буквы, которые будут использоваться для обозначения каждой переменной, их значения, а также различные свойства – например, положительную или отрицательную логическую функцию.
Далее, следует описать таблицу истинности, которая будет основой для построения карты Карно. Важно указывать все возможные комбинации значений переменных, а также соответствующие им значения функции. В этом разделе, можно использовать термины, такие как "истина" и "ложь", вместо более сложных определений.
Четкое и точное описание исходных данных является ключевым фактором для успешного создания КНФ на основе карты Карно. Предоставьте всю необходимую информацию с ясностью и последовательностью, чтобы избежать путаницы и ошибок в процессе обработки данных.
Построение самой карты Карно
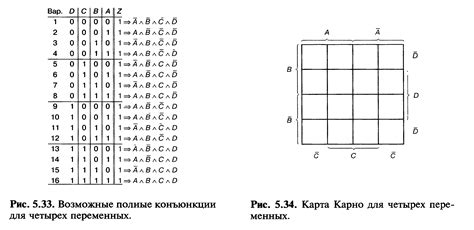
Разберемся, как создать карту Карно, необходимую для проведения минимизации логической функции.
Первоначально нужно составить таблицу истинности, в которой перечислить все возможные комбинации входных значений. Затем определить значение функции для каждой комбинации и заполнить соответствующие ячейки таблицы.
После того как таблица истинности полностью заполнена, мы можем приступить к построению самой карты Карно. Для этого необходимо разбить таблицу истинности на прямоугольные участки, размер которых определяется количеством переменных функции. Каждый прямоугольник будет представлять собой группу единиц в таблице истинности.
Как только мы разделили таблицу на прямоугольники, у нас появляются основные элементы карты Карно – квадраты. Количество квадратов равно количеству прямоугольников.
Далее необходимо объединить квадраты в группы, соседствующие по вертикали или горизонтали. Каждая группа должна содержать степень двойки переменных – 2, 4, 8 и так далее. Объединение осуществляем путем выделения общих значений в ячейках квадратов.
В результате мы получим сгруппированные квадраты, которые будут использованы для записи новой логической функции.
Порядок и принципы заполнения таблицы Карно: важные шаги и рекомендации
В данном разделе мы рассмотрим основные шаги и правила, которые следует учесть при заполнении таблицы Карно для построения КНФ. Данная таблица представляет собой инструмент, позволяющий систематизировать логические значения переменных и установить взаимосвязи между ними, что в свою очередь помогает создать удобное графическое представление булевой функции.
1. Определите количество переменных: Важным первым шагом является определение количества переменных в булевой функции. Учитывайте, что таблица Карно требует равного количества переменных и представляет собой квадратную матрицу с соответствующим количеством строк и столбцов.
2. Заполните таблицу согласно логическим значениям: В следующем шаге необходимо заполнить таблицу Карно, установив логические значения для каждой комбинации переменных. При заполнении таблицы следует придерживаться определенного порядка, начиная с первой строки и продолжая по порядку по строкам и столбцам. При этом необходимо понимать, что каждая ячейка таблицы может принимать только два возможных значения: 0 или 1.
3. Сгруппируйте ячейки с единицами: Далее следует выделить и сгруппировать ячейки таблицы, в которых значения равны 1. Каждая группа должна состоять из соседних ячеек, где изменяется только одна переменная. Группы можно формировать горизонтально или вертикально, в зависимости от удобства и сложности булевой функции.
4. Запишите конъюнкции: Последним шагом является запись конъюнкций для каждой сгруппированной области. Конъюнкция представляет собой логическое умножение переменных внутри каждой группы. Важно помнить, что каждая переменная в конъюнкции должна принимать два возможных значения: саму переменную и ее инверсию. Конъюнкция для каждой группы является одним из слагаемых формулы КНФ.
Таким образом, следуя указанным шагам и принципам заполнения таблицы Карно, вы можете создать удобное графическое представление булевой функции, которое далее будет использовано для построения соответствующей конъюнктивно-нормальной формы.
Поиск элементарных следствий на основе строения Карты Карно
Анализируя структуру Карты Карно, можно выявить особые области, называемые простыми импликантами. Эти области представляют собой уникальные комбинации ячеек с минимальным возможным числом переменных.
Процесс обнаружения простых импликантов основан на поиске замкнутых областей, содержащих достаточное количество ячеек, чтобы исключить другие возможные комбинации значений переменных. Для этого необходимо аккуратно анализировать каждую ячейку Карты Карно.
При исследовании каждой ячейки следует обратить внимание на ее соседние ячейки и определить, являются ли они частью потенциальной простой импликанты. Затем необходимо продолжать анализ постепенно, двигаясь по каждой строке и каждому столбцу Карты Карно.
Чтобы убедиться, что найдена простая импликанта, следует проверить, является ли каждая ячейка в составе выбранной области соседней с любой другой ячейкой внутри этой области. В случае, если нет никаких соседствующих ячеек, можно считать, что найдена простая импликанта.
Далее необходимо проверить, что каждая ячейка внутри простой импликанты отличается только одной переменной от соответствующей ячейки в других областях Карты Карно. Если это требование выполняется, тогда можно сказать, что простая импликанта найдена и ее компактное представление может быть использовано для формирования КНФ.
Обнаружение простых импликантов при анализе Карты Карно позволяет существенно упростить процесс построения канонической нормальной формы и получить наиболее компактное и эффективное представление логической функции.
Способы выявления необходимых клеток
В этом разделе рассмотрим различные методы определения необходимых ячеек по карте Карно без привлечения конкретных терминов и определений.
Первый способ заключается в...
- Изучении расположения символов на карте и их сдвигах
- Анализе последовательности чисел в объединенных прямоугольниках
- Учете наличия и отсутствия единиц в каждой ячейке и их взаимосвязей
- Установлении зависимостей между входными переменными и выходами
Второй способ предполагает...
- Выделение прямоугольников с минимальным числом переходов
- Поиск наиболее значимых групп ячеек
- Определение закономерностей в расположении символов и их влияния на выбор ячеек
Сравнение и комбинирование этих способов поможет максимально точно и эффективно определить необходимые клетки на карте Карно.
Составление конъюнктивной нормальной формы на основе импликант, полученных из карты Карно

Для начала необходимо проанализировать карту Карно и выявить импликанты, которые покрывают все нулевые и единичные значения функции. После этого, каждую импликанту можно рассматривать как элементарное условие, которое должно выполняться для истинности всей функции.
Далее, мы можем объединить все импликанты в КНФ, используя логическую операцию "ИЛИ". Каждая импликанта будет представлена в виде конъюнкции литералов, где литералы могут быть либо переменными, либо их отрицаниями.
Если импликантов получилось много, возможно потребуется применить процесс упрощения КНФ и выполнить минимизацию логической функции. Для этого можно использовать алгоритмы Квайна-МакКласки и метод Куайна.
Итак, составление КНФ на основе импликант, полученных из карты Карно, позволяет нам компактно и однозначно представить логическую функцию, учитывая все возможные варианты ее значений. Это является важным шагом при решении задачи поиска минимальной формы логической функции и оптимизации схемы ее реализации.
Вопрос-ответ

Можно ли использовать метод карт Карно для упрощения сложных логических функций?
Да, метод карт Карно можно использовать для упрощения сложных логических функций. Однако, порядок переменных в таблице истинности должен быть логически связным. Если в таблице присутствуют 'дыры', т.е. ячейки таблицы, в которых значение функции равно 0, то их следует объединить в отдельную группу. Также важно помнить, что число переменных должно быть степенью двойки, так как карты Карно используют двоичную систему.
Какая польза от создания КНФ с использованием метода карт Карно?
Создание конъюнктивной нормальной формы (КНФ) с использованием метода карт Карно имеет ряд преимуществ. Во-первых, это позволяет упростить сложные логические функции и сделать их более читаемыми. Во-вторых, КНФ позволяет анализировать и предсказывать поведение системы на основе истинности каждой конъюнкции, что может быть полезно при проектировании цифровых схем и устройств. Кроме того, КНФ может быть использована для проверки эквивалентности различных логических функций.
Можно ли использовать метод карт Карно для создания других нормальных форм, например, дизъюнктивной нормальной формы (ДНФ)?
Нет, метод карт Карно применяется исключительно для создания конъюнктивной нормальной формы (КНФ), которая представляет собой конъюнкцию нескольких дизъюнкций. Для создания дизъюнктивной нормальной формы (ДНФ) можно использовать другие методы, например, метод алгебраических преобразований или метод Квайна-МакКласки.