АВС - геометрическая фигура, состоящая из трех линий, соединяющих три точки. В данном изложении рассматривается треугольник, который обладает особыми свойствами. При этом одна из его сторон равна 64 единицам, что является важной особенностью данной геометрической формы.
Конкретные числовые значения могут изменяться, но предметом изучения является именно взаимосвязь и свойства треугольника, когда одна из его сторон имеет определенную длину. Это открывает возможность для анализа уникальных характеристик и особенностей данной геометрической фигуры.
Понятие треугольника и его определение
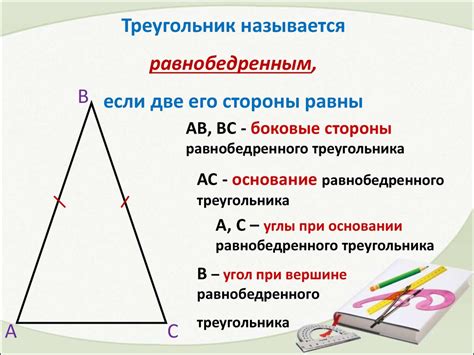
Треугольник – это плоская геометрическая фигура, образованная тремя отрезками, соединяющими три точки, называемые вершинами треугольника. Каждый отрезок, соединяющий вершины, называется стороной треугольника. Единицей измерения сторон может выступать, например, единица длины.
Каждому треугольнику присущи определенные свойства и характеристики, которые могут быть изучены и описаны при помощи математических методов и терминов. Важными характеристиками треугольника являются его периметр, площадь, углы и соотношения между сторонами и углами.
Понимание понятия треугольника и его определение является важным шагом в освоении геометрии и позволяет дальше изучать его свойства и применять полученные знания в практических задачах.
Специфика треугольника АВС с длиной стороны 64
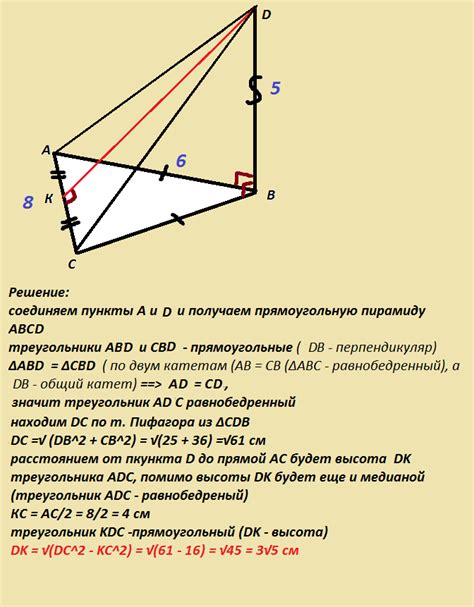
Рассмотрим особенности треугольника АВС, где одна из его сторон имеет длину 64 единицы. Этот треугольник обладает рядом уникальных свойств, которые оказывают влияние на его форму, углы и отношения между сторонами.
1. Форма треугольника: Треугольник АВС с длиной стороны 64 может принимать различные формы в зависимости от углов и длин других сторон. Его форма может быть остроугольной, тупоугольной или прямоугольной.
2. Углы треугольника: Углы треугольника АВС также зависят от длины стороны 64. Они могут быть равными или разными, и их величина определит тип треугольника. Например, в прямоугольном треугольнике один из углов будет составлять 90 градусов, а другие два угла суммируются до 180 градусов.
3. Отношения сторон: Равенство длины стороны 64 влияет на отношения между сторонами треугольника. Например, в прямоугольном треугольнике с длиной стороны 64, другие две стороны могут быть соизмеримыми или несоизмеримыми. Эти отношения могут быть использованы для вычисления других характеристик треугольника, таких как площадь и периметр.
Итак, трегуольник АВС с длиной стороны 64 является уникальным в своих форме, углах и отношениях между сторонами. Понимание этих свойств поможет вам лучше изучить и анализировать такие треугольники и применять их в практических задачах.
Применение треугольника АВС с длиной стороны 64 условные единицы в геометрии и практических задачах
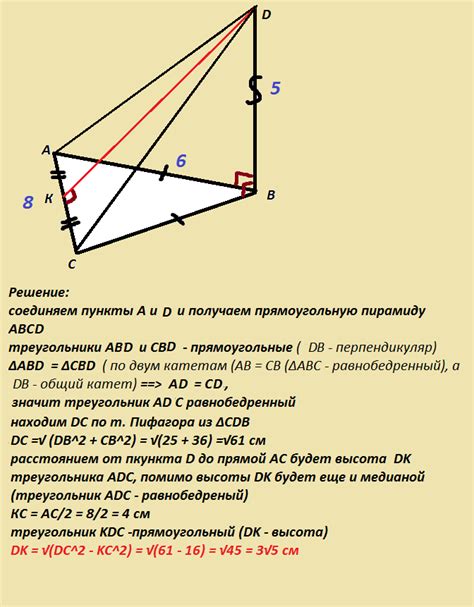
В данном разделе будут рассмотрены различные аспекты использования треугольника АВС, у которого одна из сторон равна 64 условным единицам. Рассматривая его геометрические свойства и применение в практических задачах, мы сможем лучше понять его значения и применение в различных областях.
Первоначально стоит отметить, что такой треугольник проявляет уникальные свойства, связанные с его структурой и геометрическими особенностями. Используя таблицу, можно оценить значения углов и длин других сторон, исходя из заданной длины стороны 64 условных единиц. Например, на основе теоремы косинусов можно определить длину второй стороны и углы.
| Свойства треугольника АВС: | |
|---|---|
| Длина стороны АВ: | 64 условных единицы |
| Длина стороны BC: | ... |
| Угол А: | ... |
| Угол В: | ... |
| Угол С: | ... |
Другим интересным аспектом применения треугольника АВС является его влияние на практические задачи и прикладную геометрию. Например, этот треугольник может использоваться для расчета длины недостающей стороны или определения высоты или площади подобных фигур. Его уникальные свойства позволяют решать разнообразные задачи в области конструирования, строительства, картографии и других.
В итоге, треугольник АВС со стороной длиной 64 условные единицы является предметом изучения в геометрии и активно применяется в практических задачах. Его свойства и особенности способствуют широкому разнообразию использования в различных отраслях и областях деятельности.
Вопрос-ответ

Каковы длины сторон треугольника АВС, если известно, что его периметр равен 192 единицы?
Если периметр треугольника АВС равен 192 единицам, то каждая сторона треугольника будет иметь длину 64 единицы. Поскольку периметр равен сумме длин всех трех сторон, то a + b + c = 192. Из условия известно, что a = b = c = 64, следовательно, 64 + 64 + 64 = 192.
Можно ли построить треугольник АВС, если известно, что длина одной из его сторон равна 64 единицам?
Треугольник АВС может быть построен, если известно, что длина одной из его сторон равна 64 единицам. Заданная сторона должна соответствовать условию неравенства треугольника, то есть сумма длин оставшихся двух сторон должна быть больше 64 единицы. Если это условие выполняется, то можно построить треугольник АВС.
Какие свойства треугольника можно определить при условии, что его сторона равна 64 единицы?
При условии, что сторона треугольника равна 64 единицы, можно определить различные свойства треугольника АВС. Например, можно вычислить его периметр, который будет равен 3 * 64 = 192 единицам. Также можно определить площадь треугольника, используя формулу Герона или формулу высоты. Однако для более точных вычислений необходимо знать значения других сторон или углов треугольника.
Как вычислить площадь треугольника АВС, если известно, что его сторона равна 64 единицы?
Для вычисления площади треугольника АВС, если известна только одна сторона длиной 64 единицы, необходимо знать хотя бы еще одну сторону или хотя бы один угол треугольника. Без этих данных точное вычисление площади невозможно. Однако можно использовать формулу высоты, если известна высота треугольника, проведенная к стороне АВС. В этом случае площадь будет равна половине произведения длины основания (в данном случае 64 единицы) на высоту.



