В мире искусства существует множество различных приемов и техник, позволяющих художникам передать свои идеи и эмоции на холсте. Одним из таких захватывающих приемов является создание треугольника, описанного около окружности.
Дело в том, что треугольник, как геометрическая фигура, имеет особый символический смысл, а описанная около окружности добавляет ему еще больше глубины и значимости. Это становится мощным инструментом, который художник может использовать для передачи определенных идей, а также для создания изображения, которое будет привлекать внимание зрителя и вызывать у него эмоциональный отклик.
Создание треугольника, описанного около окружности, требует некоторой технической и творческой грамотности. Художнику необходимо иметь в своем арсенале набор инструментов, позволяющих точно вычертить требуемую фигуру и добиться гармоничного сочетания цветов и линий. Более того, это требует от художника определенного знания и понимания эффектов и визуальных принципов, которые могут быть использованы для создания впечатляющего и привлекательного искусственного образа.
Необходимые инструменты и материалы для создания треугольника, описанного около окружности
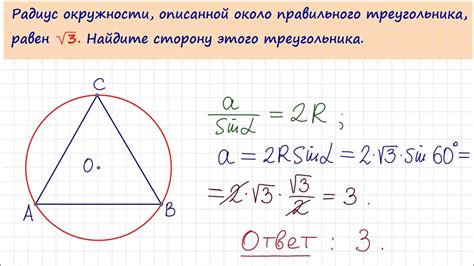
Осуществление процесса создания треугольника, описанного около окружности, требует использования определенных инструментов и материалов. Следующий список содержит необходимые предметы для успешного выполнения данной задачи.
- Геометрический циркуль - инструмент с регулируемыми ножками, при помощи которого можно создавать окружности и измерять расстояния.
- Линейка - помогает создавать прямые линии и контролировать расстояния при построении треугольника.
- Карандаш - основной инструмент для нанесения линий и отметок на бумагу.
- Ластик - используется для исправления ошибок и стирания ненужных линий.
- Бумага - подложка, на которой будет происходить рисование треугольника и операции с окружностью.
- Компас - соединяется с геометрическим циркулем для создания окружности, которая является основой для построения треугольника.
Эти инструменты и материалы играют важную роль в процессе создания треугольника, описанного около окружности. Они позволяют обозначить и измерить нужные линии и углы, обеспечивая точность и качество конечного результата.
Старт: первые шаги в создании треугольника вокруг окружности
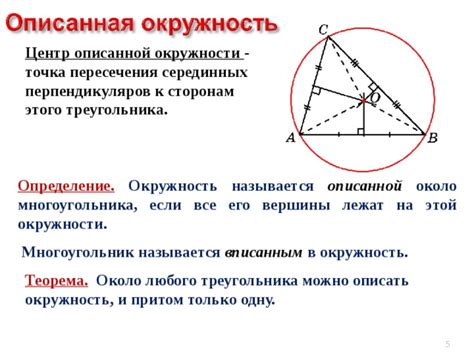
В данном разделе мы рассмотрим основы создания треугольника, описанного около окружности. Научимся шаг за шагом строить эту геометрическую фигуру без необходимости использования сложных математических определений.
Для начала работы потребуется отличное понимание геометрических соотношений и базовых терминов. Мы рассмотрим основные понятия и приемы, которые помогут в создании треугольника вокруг окружности с легкостью и точностью.
Важно разобраться с терминами, такими как радиус, диаметр и центр окружности. Также нам понадобится некоторая информация о треугольниках, их сторонах и углах. В этом разделе мы пошагово проведем вас через процесс создания треугольника, описанного около окружности, и покажем, как все эти элементы связаны между собой.
Выбор местоположения центра окружности и построение основания треугольника
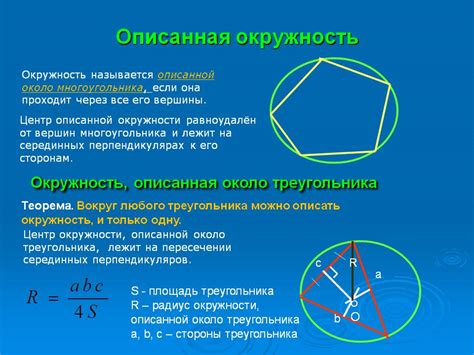
Для начала, необходимо определиться с выбором места, где будет располагаться центр окружности. Исходя из требований и целей построения треугольника, можно выбрать разные варианты для центра окружности.
- Равносторонний треугольник: для создания такого треугольника центр окружности будет располагаться в точке пересечения медиан треугольника.
- Равнобедренный треугольник: центр окружности будет лежать на высоте, проходящей через вершину равных сторон.
- Произвольный треугольник: в этом случае выбор местоположения центра окружности будет определяться исходя из желаемого расположения треугольника на плоскости и визуальных предпочтений.
После выбора местоположения центра окружности необходимо построить основание треугольника. Это может быть выполнено с использованием различных методов и инструментов, включая компас, линейку или графические программы.
Основание треугольника определяется как точка пересечения окружности, описанной вокруг треугольника, с каждой из его сторон. Для достижения эстетического эффекта рекомендуется построить треугольник таким образом, чтобы его основание было равносторонним или равнобедренным.
Определение радиуса описанной окружности
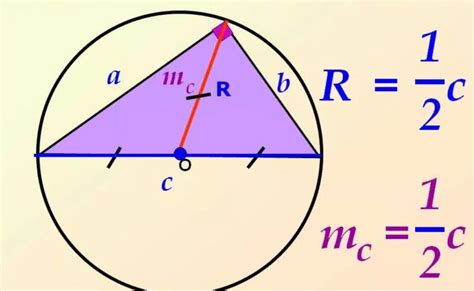
Для нахождения радиуса описанной окружности существует несколько методов, которые мы представим вам в этом разделе.
- Метод построения радиуса описанной окружности с использованием медианы треугольника.
- Метод построения радиуса описанной окружности с использованием высоты треугольника.
- Метод построения радиуса описанной окружности с использованием радиуса вписанной окружности.
- Метод построения радиуса описанной окружности с использованием длин сторон треугольника.
Каждый из данных методов представляет свою уникальную формулу, основанную на связи между различными параметрами треугольника. Рассмотрим каждый метод подробнее и предоставим примеры расчетов радиуса описанной окружности для конкретных треугольников.
Определение координат вершин треугольника

В данной части статьи мы рассмотрим способы определения координат вершин треугольника в контексте задачи описания его вписанной окружности.
Для начала, важно понять, что вершины треугольника являются точками, имеющими свои координаты на плоскости. Координаты вершин задают их положение в двумерном пространстве.
Одним из подходов к определению координат вершин треугольника является использование геометрических свойств и нахождение пересечений прямых, описывающих стороны треугольника. Также можно использовать формулу расстояния между точками для вычисления координат вершин.
Другим методом может быть использование угловых и длинных отношений в треугольнике, чтобы определить координаты вершин. Здесь важно учитывать описания задачи и наличие данных о расстоянии между вершинами и центром вписанной окружности.
Необходимо помнить, что для решения данной задачи требуется достаточное знание геометрии и умение применять соответствующие формулы и теоремы.
Построение биссектрис углов треугольника
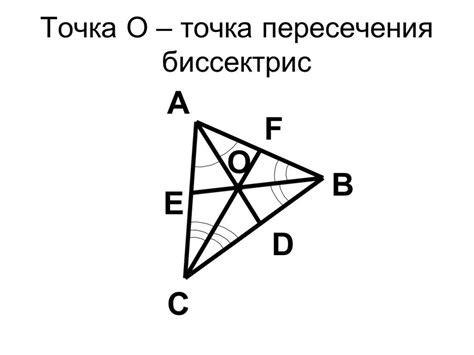
Для построения биссектрисы угла треугольника можно использовать несколько методов. Один из самых распространенных методов - это использование циркуля и линейки. В этом случае необходимо провести две дуги, с радиусами, равными расстоянию от вершины угла до сторон треугольника, и построить прямую, соединяющую точки пересечения этих дуг.
Еще одним методом является построение биссектрисы с использованием компаса и линейки. В этом случае необходимо провести две дуги с центрами в вершине угла и соединить точки пересечения этих дуг прямой.
Следует отметить, что биссектрисы углов треугольника также имеют некоторые интересные свойства, которые могут быть использованы при решении задач. Например, точка пересечения биссектрис углов треугольника является центром вписанной окружности в этот треугольник.
Использование биссектрис при построении и анализе треугольников является важным инструментом для понимания их свойств и особенностей. Такое знание может помочь при решении различных задач, связанных с геометрией, а также в дальнейшем изучении более сложных фигур и структур.
Проверка правильности построения треугольника с описанной около окружностью

Уточнение деталей и внесение изменений в фигуру

В данном разделе мы рассмотрим важные аспекты, связанные с уточнением деталей и корректировкой фигуры, описанной около окружности. Здесь мы проанализируем основные шаги и техники, которые помогут сделать фигуру более точной и симметричной.
- Точность измерений: В первую очередь необходимо обратить внимание на точность проведения измерений. Используйте инструменты, позволяющие достичь наибольшей точности, например, линейку с миллиметровой шкалой или цифровой измерительный прибор.
- Учет дополнительных параметров: При построении фигуры необходимо учитывать такие детали, как радиус окружности и площадь треугольника. Применение математических формул и учет этих параметров поможет достичь более точного и сбалансированного результата.
- Симметрия и пропорции: Одним из важных аспектов рисования фигуры является достижение симметрии и правильных пропорций. Используйте симметричные элементы и ориентируйтесь на главные пропорциональные отношения, чтобы создать эстетически приятную и гармоничную фигуру.
- Корректировка и подгонка: Во время процесса рисования может возникнуть необходимость внести корректировки и подогнать фигуру под требуемые параметры. Будьте готовы вносить изменения, используя техники, такие как растягивание, сжатие или поворот элементов для достижения желаемого результата.
- Детализация и отделка: Не забывайте о мелких деталях и отделке вашей фигуры. Уделите внимание деталям, таким как острые углы или округлые края, чтобы придать фигуре больше реалистичности и выразительности.
Уточнение деталей и корректировка фигуры являются важными этапами процесса создания треугольника, описанного около окружности. Используя описанные выше техники и следуя указаниям, вы сможете придать вашей фигуре более точную форму и достичь желаемого результата.
Подключение внешней геометрической системы

Раздел "Подключение внешней геометрической системы" представляет собой важный этап в процессе работы с геометрическими фигурами, такими как треугольник, описанный около окружности.
Геометрические системы являются неотъемлемой частью математического аппарата, позволяющего нам анализировать исследуемые фигуры и проводить соответствующие вычисления. Внешние геометрические системы представляют собой специализированные инструменты, программы или библиотеки, которые позволяют работать с геометрическими фигурами, выполнять различные операции и получать результаты в формате, удобном для дальнейшего использования.
Подключение внешней геометрической системы может быть осуществлено с помощью различных методов, включая подключение через API, использование сторонних библиотек или написание собственного кода. Каждый из этих подходов имеет свои преимущества и возможности, и выбор наиболее подходящего зависит от конкретной задачи и требований к функциональности и производительности.
Важно отметить, что выбор внешней геометрической системы должен быть основан на тщательном анализе ее возможностей, документации, поддержки и примеров использования. Эффективное использование подобных систем позволяет значительно упростить работу с геометрическими фигурами и повысить точность и надежность получаемых результатов.
Заключительные штрихи и отделка рисунка

Передавая заключительную стадию процесса, этот раздел уделит внимание важным деталям и финишной отделке рисунка, созданного на основе описанного окружности треугольника. Здесь приведены ключевые приемы и рекомендации для придания искривленных линий максимальной выразительности и эстетического совершенства.
Важным аспектом заключительных штрихов является использование акцентирования и усиления определенных элементов через линии, тени, штриховку или градиенты. Отображение объемного эффекта и текстур в рисунке может быть достигнуто с помощью специальных техник, таких как фоновая перспектива и перекрытие линий.
Рекомендуется также аккуратно подбирать цветовую гамму для рисунка, чтобы подчеркнуть его композиционные особенности и создать гармоничное визуальное впечатление. Оттенки и контрасты могут быть использованы для акцентирования конкретных частей рисунка или создания определенной атмосферы.
Заключительный этап отделки рисунка включает в себя работу над финальными деталями и доработками. Независимо от того, выбран ли традиционный инструмент или программное обеспечение для редактирования, рекомендуется уделить максимальное внимание точности и аккуратности, чтобы достичь высокого качества и завершенности результата.
Завершив этот этап, вы станете обладателем полностью доработанного и выразительного рисунка, отличающегося оригинальностью и красотой. Учтите, что практика и эксперименты ключевы для достижения желаемого результата, поэтому не бойтесь использовать творческий подход и экспериментировать с различными техниками.
Вопрос-ответ

Какими инструментами можно нарисовать треугольник, описанный около окружности?
Для рисования треугольника, описанного около окружности, можно использовать компас и линейку. Сначала нужно нарисовать окружность с помощью компаса. Затем, выбрав три точки на окружности, можно провести линии, соединяющие эти точки и получить треугольник.
Как найти центр описанной окружности треугольника?
Для нахождения центра описанной окружности треугольника можно использовать так называемую "теорему о трёх серединах". Согласно этой теореме, центр описанной окружности треугольника находится на пересечении медиан треугольника. Для нахождения центра можно провести медианы треугольника и найти их точку пересечения.
Можно ли нарисовать треугольник, описанный около окружности, без использования компаса?
Да, можно нарисовать треугольник, описанный около окружности, и без использования компаса. Например, для этого можно воспользоваться геометрическими методами. Один из вариантов - использование процесса инсайдера. В этом случае нужно провести от любой точки окружности перпендикуляры к сторонам треугольника и найти точки их пересечения с окружностью. Затем можно провести линии, соединяющие найденные точки и получить треугольник.
Для чего полезно уметь рисовать треугольник, описанный около окружности?
Умение нарисовать треугольник, описанный около окружности, полезно в геометрии и конструктивной геометрии. Такие треугольники активно используются при решении различных задач и построения различных фигур. Это является важной базовой навыком для изучения геометрии и решения геометрических задач.



