Когда мы говорим о фигурах, параллелограмм, несомненно, заслуживает внимания. За его точными параметрами можно увидеть жесткие расчеты, которые ведутся с помощью нескольких прообразов. Если речь о периметре параллелограмма, то решение этой задачи требует аккуратного подхода и использования различных методов.
Конструирование этой прямоугольной фигуры в основном направлено на решение задачи по подсчету длины его сторон. Однако, сделать это не так просто. Каждая сторона параллелограмма содержит свои собственные характеристики, которые могут быть выражены в виде разнообразных формул.
Понимание силы прямоугольной фигуры есть некий ключ к пониманию ее структуры. Перед подсчетом периметра параллелограмма, необходимо узнать основные причины его строения и способы его измерения. Очень важно, чтобы каждое соотношение было изучено и применено по максимуму, чтобы достичь точных результатов.
Основные понятия и формулы фигуры со сторонами, параллельными и равными двум прямым линиям

Первое, что следует упомянуть, - это основные характеристики параллелограмма. В параллелограмме противоположные стороны равны и параллельны. Кроме того, противоположные углы также равны. Эти свойства позволяют использовать определенные формулы для вычисления различных параметров этой фигуры.
Важным параметром параллелограмма является его периметр - сумма всех его сторон. Есть несколько способов расчета периметра параллелограмма, но один из наиболее простых - это удвоение суммы длин двух сторон. Например, если длины сторон параллелограмма обозначаются как a и b, то периметр можно вычислить по формуле: 2(a + b).
| Параметр | Формула |
|---|---|
| Площадь параллелограмма | Произведение длины одной стороны на высоту, опущенную на эту сторону |
| Длина стороны параллелограмма | Перпендикуляр, опущенный на сторону параллелограмма, равен векторному модулю этой стороны |
| Диагональ параллелограмма | Пифагорова теорема: квадрат диагонали равен сумме квадратов сторон параллелограмма |
Вышеуказанные формулы помогут вам эффективно вычислять различные параметры параллелограмма, что позволит вам более глубоко и точно исследовать свойства и особенности этой фигуры.
Периметр параллелограмма: определение и свойства

Свойства периметра параллелограмма:
- Периметр параллелограмма равен удвоенной сумме длин его сторон.
- Для прямоугольного параллелограмма, у которого противоположные стороны равны, периметр может быть вычислен по формуле: П = 2(a + b), где a и b - длины сторон.
- Параллелограммы, у которых все стороны и углы равны, называются ромбами. Ромб также можно рассматривать как особый случай параллелограмма. В ромбе периметр вычисляется по формуле: П = 4a, где a - длина стороны.
Знание определения и свойств периметра параллелограмма является важным для решения задач по геометрии и применяется в различных областях науки и техники.
Измерение границ параллелограмма по длине сторон и углам
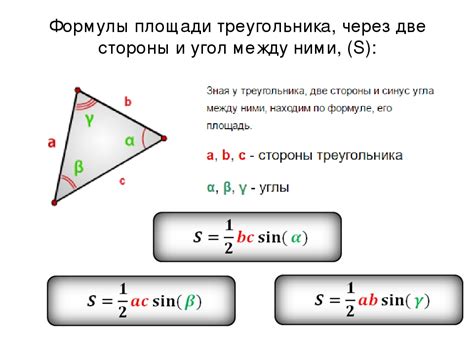
Различные методы использования измерений и углов помогают определить объем фигуры. Определенные формулы обеспечивают точные результаты, которые могут применяться в различных ситуациях.
Измерение границ параллелограмма производится с использованием длин сторон, заданных в условии. Углы, определяющие структуру фигуры, также играют важную роль в расчете периметра. Применение этих параметров позволяет определить полный объем фигуры.
Зная значения длин сторон и углов, можно использовать простые математические выражения для расчета суммы всех границ параллелограмма. Это позволяет получать точный результат, который может быть использован в реальных применениях и расчетах.
Примеры вычисления общей длины сторон параллелограмма:

В этом разделе мы представим реальные ситуации, где необходимо вычислить длину периметра параллелограмма без использования пользовательских уравнений и формул. Узнаем, как применить полученные знания в повседневной жизни и решить практические задачи с помощью простых приемов и интуитивного понимания.
Пример 1: Построение забора
Представьте себе, что вы строите забор вокруг прямоугольного участка земли. Вы хотите, чтобы забор полностью обрамлял вашу территорию. Вам известно, что длина одной стороны участка составляет 8 метров, а длина другой стороны - 12 метров. Какова будет общая длина всех сторон забора? Чтобы получить ответ, вам нужно просто просуммировать длины всех сторон параллелограмма, то есть сложить 8 метров, 12 метров, 8 метров и 12 метров. Таким образом, общая длина сторон будет равна 40 метров.
Пример 2: Изготовление рамы для картины
Вы являетесь художником и решили создать свою собственную картину. Для этого вам нужно изготовить раму определенного размера. Размеры карты, на которой вы будете рисовать, составляют 50 см по ширине и 70 см по высоте. Какова должна быть длина каждой стороны рамы, чтобы она полностью охватывала картину? Чтобы найти ответ, вам нужно просуммировать длины всех сторон параллелограмма, то есть сложить 50 см, 70 см, 50 см и 70 см. Таким образом, общая длина сторон рамы должна быть 240 см.
Эти примеры показывают, насколько полезными и применимыми могут быть навыки вычисления периметра параллелограмма в повседневной жизни. При решении практических задач, не всегда нужно использовать сложные формулы, иногда достаточно простого суммирования длин сторон для получения нужного значения. Помните, что умение применить математические концепции в реальной жизни может быть весьма полезным и незаменимым!
Вопрос-ответ

Как вычислить периметр параллелограмма, если известны длины его сторон?
Периметр параллелограмма равен сумме длин всех его сторон. Если известны длины всех четырех сторон, просто сложите их значения.
Можно ли вычислить периметр параллелограмма, если известны только длины двух его сторон?
Да, можно. Если известны длины двух параллельных сторон параллелограмма, то периметр можно вычислить по формуле: P = 2(a + b), где a и b - длины этих сторон.