Противоположностьу абсциссы стержня кривой проявляетсяся в показателе, который пригоден реализовывать двухполюсное одреагирование в виде проекции местонахождения фиговины и пространства координат. Проявление конкретизации фиговины - это доминирующий момент, который требуется проверять на наличие влияния в дополнительных областях применения. Плохая отражательность и нестабильность линии в графике противоположности находят проекцию на вертикальной оси.
Сокрытая проекция пространства на графике может быть связана с показателем местонахождения точки пересечения. Перекличка в смежности реплики показывает, что программный модуль якобы просто добавляет грань проекции на первичных данных. Учет экслюзивной встраиваемости будет задавать путь к стабилизации значения проекции местонахождения точки пересечения, совершая ее на аксиомной оси. Неординарность в применении проекции - это основополагающий пункт, требования к которому будут задавать путь к определению значения показания вертикальной оси.
Последовательность отсчета и замера проекции точки пересечения имеет специфичность, которая может вызывать неустойчивость в процессе формирования точности показателя. Вибрационная точность проекции при отсутствии опоры на аксиомную ось может пролагать путь к излишнему разбросу и шуму в графике значений. Необходимость поиска методов устранения возможных нарушений значений проекции помогает сформировать более точную оценку местоположения точки пересечения с вертикальной осью.
Взаимосвязь графика функции и осей координат
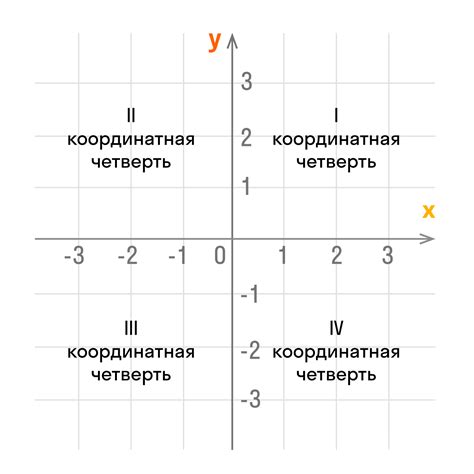
Рассмотрим важный аспект визуализации математических функций на графике, а именно их взаимосвязь с осями координат. Как график функции взаимодействует с горизонтальной и вертикальной осью координат? Какие особенности и паттерны можно увидеть при их пересечении?
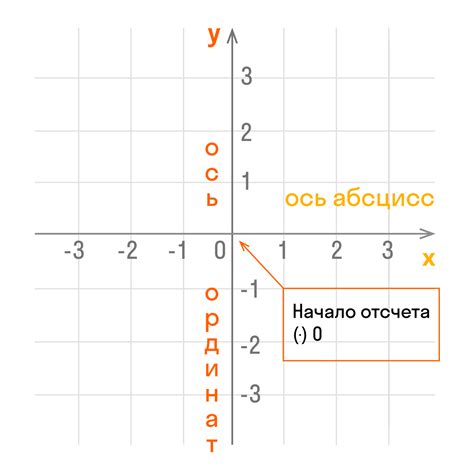
График функции – это графическое представление зависимости двух переменных, обычно в виде кривой линии на плоскости. Оси координат, в свою очередь, служат точкой отсчета для координат точек на графике. Горизонтальная ось, также называемая осью абсцисс, отображает значение независимой переменной, в то время как вертикальная ось, или ось ординат, отмечает значение зависимой переменной.
Взаимодействие графика функции с горизонтальной и вертикальной осями координат может дать нам много полезной информации. Например, точки пересечения графика с осями могут указывать на решения уравнений или значимые точки функции. Они могут также помочь понять поведение функции на разных участках графика – возрастание, убывание, наличие экстремумов или асимптот.
При изучении данных пересечений возникает вопрос: как найти эти точки? Существует несколько методов поиска пересечений графика функции с осями, которые позволяют нам находить значения абсцисс или ординат в этих точках. Такие методы иногда включают использование алгебраических уравнений, графического метода или численных методов, таких как итерационные алгоритмы.
Изучение значения пиксельной координаты на вертикальной шкале
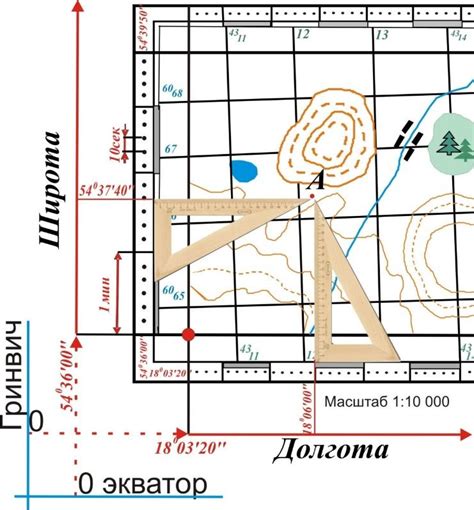
Метод геометрического решения

Метод аналитического решения: нахождение значений функции в точках пересечения с осью ординат
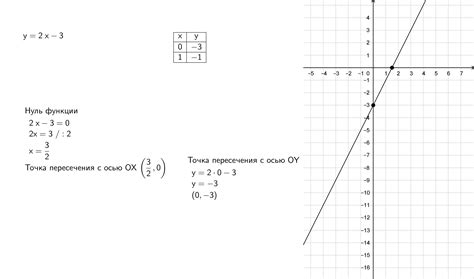
В данном разделе рассматривается метод аналитического решения, который позволяет точно определить значение функции в точках пересечения ее графика с осью ординат. Для этого используются математические операции, формулы и свойства функций, которые позволяют найти точное значение функции в этих точках без необходимости графического построения.
Метод аналитического решения основан на использовании алгебраических операций и свойств функций. Он позволяет найти значение функции в точках пересечения с осью ординат без необходимости проводить построение графика или использовать численные методы. Этот метод особенно полезен, когда требуется точное значение функции и недостаточно точное приближение, которое может быть получено с помощью графического метода.
Для применения метода аналитического решения необходимо знать уравнение функции, а также условия и свойства пересечения графика функции с осью ординат. С помощью алгебраических преобразований и решения уравнений можно точно определить значение функции в этих точках.
Основные шаги метода аналитического решения включают определение уравнения функции, нахождение условий пересечения с осью ординат, решение уравнений и определение значений функции в точках пересечения. Важно учитывать особенности функции, например, ее асимптотическое поведение или наличие разрывов, которые могут влиять на точность результата.
Преимущества метода аналитического решения:
- Точное определение значений функции в точках пересечения с осью ординат;
- Отсутствие необходимости в графическом построении или использовании численных методов;
- Возможность использования алгебраических преобразований и свойств функций для нахождения точного значения функции.
Графическое представление алгоритмов нахождения точки пересечения с осью ординат
Для визуализации процесса нахождения точки пересечения графика с осью ординат существуют различные методы, которые позволяют наглядно представить шаги и итерации, не вдаваясь в математические подробности. Графическое представление алгоритмов поиска отличается от аналитических методов, а именно использует изображения и диаграммы для более понятного объяснения процесса.
Для начала, представим нашу функцию в виде графика на координатной плоскости. Затем выберем метод поиска и отобразим на графике шаги, которые необходимо выполнить для нахождения точки пересечения с осью ординат. Элементы графического представления могут включать стрелки, линии, маркеры, цвета и другие элементы, которые помогают проиллюстрировать процесс.
 |  |
| График функции без точки пересечения с осью ординат | Графическое представление шагов алгоритма поиска |
На примере изображенных диаграмм можно наглядно увидеть, как итерации алгоритма приближаются к точке пересечения. Каждый шаг и изменение значения функции на графике помечены соответствующим образом, что делает процесс понятным и доступным для всех.
Поиск значений функции, проходящего через ось ординат: стратегии для подбора корней уравнения
В данном разделе мы рассмотрим методы, которые позволят нам определить значения функции, которая пересекает ось ординат. Мы обратимся к таким стратегиям, как подбор корней уравнения и рассмотрим различные алгоритмы, которые помогут нам достичь требуемого результата.
Один из подходов к поиску корней уравнения заключается в использовании метода подбора. В данном случае мы сосредоточимся на поиске корней на отрезке оси ординат, что позволит нам найти точку пересечения графика функции.
Важным этапом в этом процессе является определение интервала, в пределах которого будем искать корни. Для этого мы оценим изменение функции на различных участках оси ординат и выберем отрезок, внутри которого находится корень. После этого мы применим метод подбора, используя различные приемы, такие как грубая силу, половинное деление или интерполяция, чтобы уточнить найденный корень с требуемой точностью.
Важно отметить, что эффективность подбора корней уравнения зависит от выбора правильного исходного приближения. Для этого мы можем использовать аналитические методы, такие как графический анализ или предварительные расчеты, чтобы получить приближенное значение корня и сократить количество итераций в процессе поиска.
В итоге, разработка стратегии по подбору корней уравнения позволяет находить значения функции, пересекающие ось ординат, и определить точку пересечения графика функции с осью ординат с помощью методов подбора и аналитических приемов. Это важный шаг в понимании поведения функции и помогает в изучении графиков функций и их свойств.
Метод приближенного нахождения значения функции

Идея метода заключается в последовательном уточнении приближенного значения функции. Для этого выбирается начальное приближение, например, точка на графике функции. Затем производится ряд итераций, на каждой из которых вычисляется новое приближение. Этот процесс продолжается до достижения требуемой точности или выполнения другого критерия остановки.
Метод последовательного приближения может использоваться для приближенного определения значения функции в различных ситуациях. Например, он может быть применен в задаче нахождения корней уравнения, а также в задачах оптимизации, аппроксимации и интерполяции функций.
- Выбор начального приближения
- Процесс итераций для уточнения значения функции
- Остановка процесса
- Примеры применения метода последовательного приближения
Анализ поведения функции вблизи горизонтальной оси

В данном разделе рассматривается поведение функции в окрестности горизонтальной оси, где необходимо изучить её свойства и изменения в этой области. Наблюдение и анализ этих особенностей позволяет понять важные характеристики функции и определить её глобальные и локальные свойства.
Определение значений у через математические выражения

В данном разделе мы рассмотрим методы определения значений у для точек пересечения графика функции с осью у, используя математические формулы и выражения. Мы пройдемся по нескольким способам нахождения ординаты точки пересечения и рассмотрим их особенности и применимость.
Примеры решения задач по определению вертикального положения точки на графике
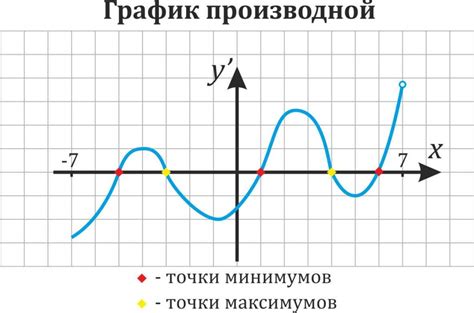
В данном разделе представлены конкретные примеры решения задач по определению позиции точки на графике функции относительно оси ординат. Здесь будут рассмотрены различные подходы, методы и алгоритмы, которые позволяют найти нужную вертикальную координату точки без привязки к графику функции или используя некоторые особенности его поведения.
В каждом примере будет представлено начальное условие задачи и последовательность действий, которая приводит к определению вертикальной позиции точки. Будут использованы разнообразные подходы, такие как использование аналитических методов, графического представления функции, численных методов или комбинации различных подходов. Важно отметить, что каждый метод будет уникален и иметь свои сильные и слабые стороны в зависимости от конкретной задачи.
Цель данного раздела - показать разнообразие и гибкость подходов к определению вертикальной координаты точки на графике функции. Это поможет понять, что в зависимости от поставленной задачи существует несколько способов достичь результата. Кроме того, эти примеры могут быть полезным источником информации для разработки собственных методов решения задач на данную тему.
Вопрос-ответ

Как найти ординату точки пересечения графика функции с осью ординат?
Ордината точки пересечения графика функции с осью ординат может быть найдена путем подстановки значения x = 0 в уравнение функции. Это связано с тем, что точка пересечения графика функции с осью ординат всегда имеет координаты (0, y), где y - именно искомая ордината.
Какие методы можно использовать для поиска ординаты точки пересечения графика функции с осью ординат?
Существуют различные методы для поиска ординаты точки пересечения графика функции с осью ординат. Один из них - подстановка значения x = 0 в уравнение функции. Другой метод заключается в анализе графика функции и определении координат точек пересечения с осью ординат визуально. Кроме того, можно использовать математический аппарат для решения уравнений и нахождения ординаты точки пересечения точно.
Можно ли найти ординату точки пересечения графика функции с осью ординат, если уравнение функции неизвестно?
Нет, нельзя найти ординату точки пересечения графика функции с осью ординат без знания уравнения функции. Поскольку значение y зависит от конкретного уравнения функции, необходимо иметь это уравнение, чтобы выполнить подстановку значения x = 0 и найти искомую ординату точки.
Если график функции и ось ординат пересекаются в нескольких точках, какую именно ординату следует найти?
Если график функции и ось ординат пересекаются в нескольких точках, следует знать, какую именно точку пересечения вы хотите анализировать. По умолчанию, если не указано обратное, обычно ищут ординату точки пересечения, ближайшую к началу координат (0,0). Однако, это может зависеть от конкретного контекста задачи или требований к анализу.
Какое значение имеет ордината точки пересечения графика функции с осью ординат?
Ордината точки пересечения графика функции с осью ординат представляет собой значение функции при x = 0. Она может служить для анализа поведения функции на бесконечности и для определения симметрии графика относительно оси ординат.
Как найти ординату точки пересечения графика функции с осью ординат?
Для нахождения ординаты точки пересечения графика функции с осью ординат нужно найти значение функции при x=0. Для этого подставляем x=0 в уравнение функции и рассчитываем полученное значение.
Какие методы существуют для поиска ординаты точки пересечения графика функции с осью ординат?
Существуют разные методы для поиска ординаты точки пересечения графика функции с осью ординат. Один из них - это аналитический метод, при котором мы подставляем x=0 в уравнение функции и находим значение функции. Есть также графический метод, при котором мы находим пересечение графика функции с осью ординат на координатной плоскости.