В увлекательной области геометрии существует важное понятие равенства фигур, которое позволяет нам сравнивать и классифицировать их. Однако, для того чтобы установить, что две фигуры являются равными, необходимо использовать эффективные методы и правила. Сегодня мы погрузимся в мир геометрии и исследуем различные подходы к определению равенства фигур.
Понимание равенства фигур является одним из фундаментальных навыков при изучении геометрии. Это позволяет нам узнавать, что две фигуры имеют одинаковую форму и размеры, что все их соответствующие стороны и углы равны. Такой уровень понимания помогает нам решать разнообразные задачи и строить логические доказательства в геометрических конструкциях.
Существует несколько подходов к определению равенства фигур в геометрии. Одним из самых распространенных методов является метод сравнения сторон и углов. Если все стороны и углы одной фигуры соответствуют соответствующим сторонам и углам другой фигуры, то эти фигуры считаются равными. Однако, этот метод не всегда эффективен, особенно при работе с более сложными и абстрактными фигурами.
Методы выявления равенства геометрических фигур на основе их свойств
В данном разделе мы рассмотрим различные подходы и методы для определения равенства геометрических фигур на основе их геометрических свойств. Каждая фигура обладает уникальными характеристиками, которые могут быть использованы для определения ее равенства другим фигурам.
- Сравнение сторон и углов
- Подобие фигур
- Совпадение элеменов
- Изометричные преобразования
Если фигуры имеют одинаковое соотношение сторон и углов, то они являются подобными. Подобные фигуры могут быть разных размеров, но все равно считаются равными.
В некоторых случаях фигуры могут быть равными, если они имеют несколько совпадающих элементов, таких как радиусы, диаметры, высоты и т.д. При наличии всех совпадающих элементов можно гарантированно утверждать о равенстве данных фигур.
Изометричные преобразования, такие как сдвиг, поворот и отражение, могут применяться для установления равенства фигур. Если две фигуры могут быть превращены друг в друга с помощью этих преобразований, то они считаются равными.
Правила эквивалентности геометрических фигур в евклидовой геометрии

Еквивалентность фигур - это понятие, отражающее их сходство или идентичность. Для определения эквивалентности фигур существуют несколько основных правил и приемов, которые позволяют оперировать взаимными отношениями между элементами геометрических фигур.
Перестановочное правило является одним из критериев для определения эквивалентности фигур. Согласно этому правилу, если порядок соответствующих элементов двух фигур может быть изменен без изменения самой фигуры, то эти фигуры считаются эквивалентными.
Гомотетическое правило основано на понятии подобия фигур. Если одна фигура может быть получена из другой путем гомотетии (масштабирования с сохранением пропорций), то эти фигуры считаются эквивалентными.
Правило равенства сторон и углов также является важным критерием эквивалентности фигур. Если у двух фигур все стороны и углы равны попарно, то эти фигуры считаются эквивалентными.
Правила эквивалентности фигур в евклидовой геометрии позволяют не только классифицировать фигуры и устанавливать их взаимные отношения, но и применять различные методы решения задач, в которых требуется определить равенство геометрических фигур.
Применение симметрии в определении эквивалентных форм

Используя концепцию симметрии, мы можем сравнивать фигуры, опираясь на их узоры, структуры и расположения элементов. В основе данного подхода лежит представление о том, что эквивалентные фигуры обладают одинаковыми симметричными свойствами, которые могут быть отражены, повернутыми или перенесены друг в друга без искажений.
Применение симметрии в определении эквивалентных форм позволяет сократить время и усилия при классификации и анализе объектов, тогда как традиционные методы требуют точных измерений и затрат на математические расчеты. Методы анализа симметрии основаны на таких понятиях, как оси симметрии, плоскости симметрии или центральной симметрии, и позволяют обнаруживать скрытые особенности и закономерности в структуре изучаемых фигур.
Методы сопоставления геометрических параметров фигур
Один из основных методов сопоставления фигур - это сравнение их габаритных параметров, таких как длина, ширина и высота. Это позволяет установить их пропорциональное соотношение друг относительно друга. Также можно рассмотреть сравнение площадей фигур, которое дает представление о их относительной поверхности. Другими словами, сравнение габаритов позволяет определить различные стороны форм и их соотношение между собой.
Для более точного определения сходства фигур часто используется сравнение их геометрических параметров, таких как радиусы, диаметры, углы и длины дуг. Эти параметры характеризуют форму фигуры более детально и позволяют выделить особенности их структуры. Кроме того, сравнение углов и длин дуг дает возможность выделить особенности геометрической формы и определить сходство или отличия между фигурами.
Дополнительно, методы сравнения фигур могут включать анализ их центральных точек, симметрии и высоты. Эти характеристики позволяют определить, насколько симметричная и уравновешенная фигура, а также установить соотношение их осей симметрии. Также можно использовать сопоставление величин высот фигур, что позволяет выявить различия в их геометрической структуре и форме.
- Сравнение габаритных параметров фигур
- Сопоставление геометрических характеристик: радиусы, диаметры, углы, длины дуг
- Анализ центральных точек, симметрии и высоты
Важность угловых свойств при определении одинаковых фигур
Одним из ключевых примеров угловых свойств, которые играют важную роль в определении равных фигур, является свойство равных углов. Если две фигуры имеют одинаковые углы, то с большой вероятностью можно утверждать, что они равны друг другу. Это свойство позволяет сократить число параметров для сравнения и сконцентрироваться на углах, что значительно упрощает процесс определения одинаковости фигур.
Кроме того, угловые свойства включают в себя такие элементы, как смежные и вертикальные углы, дополнительные и суплементарные углы, углы симметрии и другие. Все они играют свою уникальную роль в определении равности фигур и обеспечивают дополнительные признаки для сравнения и классификации геометрических объектов.
- Важность угловых свойств при определении равных фигур
- Углы фигур как "отпечатки" их равенства
- Роль свойств равных углов в процессе определения одинаковых фигур
- Дополнительные угловые свойства и их вклад в классификацию фигур
Анализ особенностей равных фигур с помощью сопоставления сторон и углов
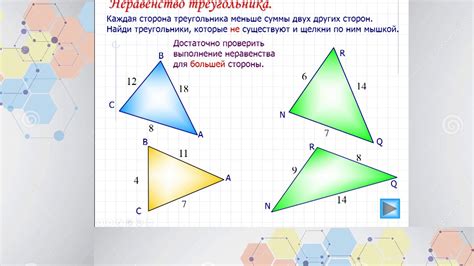
В данном разделе мы рассмотрим методы и подходы к анализу равных фигур, используя сопоставление их сторон и углов. Такой анализ позволяет нам выявить особенности и сходства между фигурами без применения конкретных определений, а именно, сравнивать их геометрические характеристики.
Сопоставление сторон является одним из ключевых способов анализа равных фигур. При сравнении фигур мы обращаем внимание на длины и соотношения их сторон, а также на их положение относительно друг друга. Точное измерение сторон позволяет нам установить, являются ли фигуры равными или разными, а также определить тип их симметрии.
Сравнение углов также играет важную роль в анализе равных фигур. Углы являются основными элементами геометрических фигур и могут предоставить нам информацию о сходствах и различиях между ними. При сопоставлении углов мы обращаем внимание на их величину, форму и положение внутри фигур.
Кроме того, важно учитывать, что для успешного анализа равных фигур необходимо использовать систематический подход. Комбинирование сопоставления сторон и углов позволяет нам получить полную картину сходств и различий между фигурами, а также определить их равенство.
- Рассмотрение длин сторон и их соотношение
- Идентификация симметричных элементов
- Анализ формы и величины углов
- Использование систематического подхода
Использование подобия фигур для определения их эквивалентности
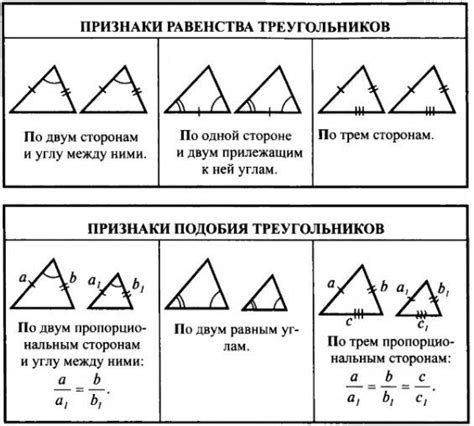
Основным преимуществом использования подобия для определения равенства фигур является возможность сокращения временных и ресурсных затрат. Вместо того, чтобы проводить точные измерения и сравнивать полученные значения, можно использовать сходство фигур и устанавливать их эквивалентность на основе данных о пропорциональности углов и сторон.
Важным аспектом использования подобия фигур является выбор основания для сравнения. Обычно в качестве основания берется какой-либо угол или сторона фигуры. Основание должно быть явно определено и представлено в качестве сравнительного параметра при сравнении фигур. Например, можно выбрать основанием фигуры наибольший угол или длину наибольшей стороны, и на основе этого сравнить подобные фигуры.
Влияние размерности пространства на выявление одинаковых форм
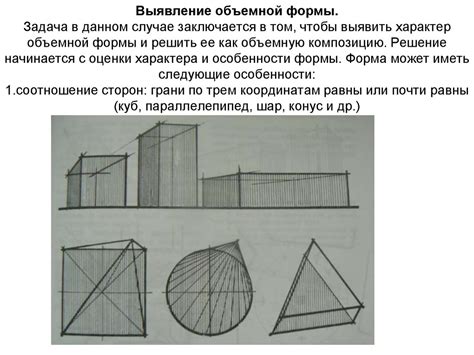
Размерность пространства играет существенную роль в определении равности фигур. В зависимости от количества измерений, наши способности воспринимать и сравнивать формы могут значительно меняться.
В двухмерном пространстве, где фигуры описываются только двумя координатами, мы можем обращать внимание на их геометрические свойства, такие как длины сторон и углы между ними. При этом мы ориентируемся на простые правила сравнения исходя из наших знаний о плоской геометрии.
Однако в трехмерном пространстве, где фигуры описываются тремя координатами, наше восприятие и анализ становятся более сложными. Мы начинаем обращать внимание не только на длины, но и на объемы фигур, а также на их ориентацию и пространственное положение друг относительно друга. Тут мы уже применяем более сложные алгоритмы и методы сравнения для определения равенства форм.
В многомерном пространстве, где фигуры описываются более чем тремя координатами, возникают дополнительные сложности. Мы должны учитывать большее количество характеристик, таких как радиусы, диагонали, площади поверхностей и т.д. Также нам может потребоваться использование специальных математических моделей и техник для более точного сравнения форм, что делает процесс более ресурсоемким.
Итак, размерность пространства имеет прямое влияние на нашу способность определять равность фигур. Чем выше размерность, тем больше характеристик приходится учитывать и тем сложнее процесс сравнения. Поэтому необходимо адаптировать методы и правила определения равных фигур в зависимости от размерности пространства.
Роль преобразований в определении одинаковых фигур
В данном разделе рассмотрим значение преобразований при определении одинаковых фигур. Преобразования играют важную роль в анализе и сравнении геометрических объектов, позволяя выявить их одинаковость без необходимости точного сравнения каждой составляющей элемента.
Преобразования, такие как повороты, отражения и сдвиги, позволяют трансформировать фигуру, сохраняя при этом ее форму и размеры. Это позволяет нам перейти от одной фигуры к другой, не изменяя их существенных характеристик.
Применение преобразований позволяет упростить процесс определения одинаковых фигур, основанный на анализе их свойств. Например, если две фигуры можно получить друг из друга с помощью поворотов, то они считаются одинаковыми. Такой подход помогает исключить множество ненужных сравнений и сосредоточиться на более существенных аспектах, таких как количество сторон или углов у фигуры.
Преобразования также позволяют выделить инвариантные свойства фигур - те характеристики, которые остаются неизменными при преобразовании. Например, длина сторон и углы между ними являются инвариантными свойствами, которые могут быть использованы при сравнении фигур. Это помогает выявлять равные фигуры даже в случаях, когда они находятся в различных ориентациях или находятся внутри других фигур.
Таким образом, преобразования играют важную роль при определении одинаковых фигур, позволяя нам сосредоточиться на главных характеристиках и облегчая процесс сравнения и анализа.
Применение понятия эквивалентности в геометрических расчетах

Понятие эквивалентности в геометрии означает, что две фигуры могут быть считаться равноценными, если они имеют одинаковую форму, размеры и ориентацию в пространстве. Это позволяет использовать свойства одной фигуры для определения свойств другой, что существенно упрощает геометрические вычисления.
В геометрии часто возникает задача определения площади, периметра, объема или других характеристик фигуры. Применение понятия эквивалентности позволяет свести сложные вычисления к более простым, используя уже известные свойства равноценных фигур.
Например, если у нас есть прямоугольник, площадь которого найти сложно, можно заменить его на равноценный прямоугольник с более простыми размерами, такими как ориентация сторон или отношение их длин. Затем можно использовать известные формулы для вычисления площади прямоугольника с простыми размерами и применить полученный результат к исходной фигуре.
Вопрос-ответ

Какие методы можно использовать для определения равных фигур?
Для определения равных фигур можно использовать различные методы, включая сравнение сторон и углов, использование геометрических преобразований, а также применение формул и теорем.
Какие правила следует придерживаться при определении равных фигур?
При определении равных фигур следует придерживаться нескольких правил. Во-первых, стороны и углы должны быть одинаковыми. Во-вторых, фигуры должны иметь одинаковую форму и размер. Также, если одна фигура может быть превращена в другую с помощью сдвига, поворота или отражения, то они считаются равными.