Геометрия является одним из важнейших разделов математики, который позволяет нам разбираться во всем окружающем нас пространстве. В 7 классе мы начинаем углублять свои знания в геометрии и изучаем такое важное понятие, как "луч".
Луч - это одна из основных составляющих геометрических фигур, которая выступает в качестве вектора движения, направляющего наше внимание к определенному объекту. Но что именно представляет собой луч, и каким образом мы можем его определить? Давайте разберемся.
Луч в геометрии - это утонченная стрелка, указывающая на конечную точку. Он начинается от определенной точки, которую мы называем началом луча, и продолжается в определенном направлении, не имея конкретной конечной точки. Важно отметить, что луч имеет только одно направление и не ограничен конечной точкой.
Изучение лучей играет важную роль в геометрии, так как их свойства и характеристики позволяют нам лучше понять взаимосвязь между различными геометрическими фигурами и помогают нам строить логические цепочки при решении геометрических задач. Понимание понятия луча открывает перед нами новые возможности в анализе и построении геометрических моделей.
Геометрия: фундаментальные понятия и их роль в учебной программе 7 класса

Фигура - это объемное или плоское образование, определенное границей или контуром. В геометрии фигуры делятся на плоские и объемные. Плоские фигуры возникают при пересечении плоскости плоской кривой или прямолинейной линией. Они имеют только две измерения - длину и ширину. Объемные фигуры обладают также третьим измерением - высотой, они занимают объем и могут быть реальными объектами, такими как куб, сфера или пирамида.
Угол - это область пространства между двумя лучами, исходящими из одной точки. Углы используются для описания поворотов, направлений и отношений между линиями. Они могут быть различных видов: острые (меньше 90 градусов), прямые (равны 90 градусам) и тупые (больше 90 градусов). Углы также могут быть смежными, вертикальными или суплементарными в зависимости от их положения и характеристик.
Параллельные прямые - это прямые, которые лежат в одной плоскости и никогда не пересекаются. Если две прямые параллельны, то они имеют одинаковое направление и расстояние между ними всегда одинаково. Параллельные прямые используются в геометрии для определения отношений между углами, построения параллельных линий и решения задач на построение фигур.
Однако, это лишь отдельные примеры понятий, которые ученики изучают в 7 классе. Геометрия раскрывает перед нами богатство форм, исследование которых расширяет наши знания о мире и помогает развить логическое мышление и способность видеть связи между абстрактными объектами.
Основные понятия и базовые определения в геометрии

Точка - это одномерный геометрический объект, который не имеет ни размеров, ни формы, ни направления. Он является основным строительным элементом всей геометрии и служит для определения других геометрических объектов.
Прямая - это одномерное множество точек, которое не имеет начала, конца и ширины. Прямая расширяется в обе стороны до бесконечности и может быть задана посредством двух точек или одной точки и направления.
Отрезок - это часть прямой, образованная двумя точками. Отрезок имеет начало и конец и является конечным по длине.
Угол - это фигура, образованная двумя лучами, которая пространственно ограничена и может быть измерена в градусах. Угол определяется своей вершиной и двумя сторонами - лучами.
Параллельные прямые - это прямые, которые лежат в одной плоскости и не пересекаются независимо от их продолжения. Они имеют одно и то же направление и постоянное расстояние между собой.
Перпендикулярные прямые - это прямые, которые пересекаются и образуют прямой угол (угол в 90 градусов). Они имеют противоположные направления.
Знание этих основных понятий и определений поможет вам строить геометрические конструкции, формулировать и доказывать теоремы, а также решать задачи, связанные с геометрией.
Углы и их классификация
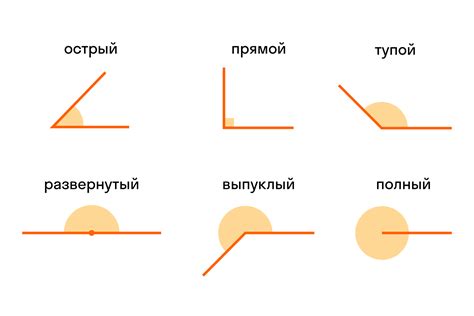
В геометрии углы играют важную роль, так как они определяют взаимное положение прямых и плоскостей. Понятие угла позволяет изучать и анализировать фигуры и их свойства. В данном разделе мы рассмотрим основные понятия, связанные с углами, а также классификацию углов в зависимости от их вида и размера.
Угол - это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. Первый луч называется начальной стороной, а второй - конечной стороной. Важно понимать, что углы могут иметь различные размеры и положения, что влияет на их классификацию и свойства.
Существует несколько способов классифицировать углы. Одним из ключевых критериев является их размер. Углы, чьи стороны лежат на прямых, называются прямыми углами и равны 90 градусам. Острые углы имеют размер меньше 90 градусов, а тупые углы - больше 90 градусов.
Кроме размера, углы также могут быть классифицированы по своему положению друг относительно друга. Например, вертикальные углы образуются пересечением двух прямых и находятся по разные стороны от пересекающейся прямой. Смежные углы располагаются по соседству и имеют общую начальную или конечную сторону. Дополнительные углы составляют в сумме 180 градусов и находятся по разные стороны от пересекающейся прямой в паре с вертикальными углами.
Изучение углов и их классификация позволяют нам анализировать и решать различные геометрические задачи. Понимание свойств углов помогает строить более сложные фигуры и доказывать различные геометрические теоремы.
Треугольники: основные свойства и типы

Первое свойство треугольника - его сумма углов всегда равна 180 градусам. То есть, если мы измерим углы треугольника и сложим их, получим 180 градусов. Второе свойство - сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это неравенство называется неравенством треугольника. Третье свойство - среди всех треугольников с заданными сторонами, наибольшую площадь имеет равносторонний треугольник, у которого все стороны равны.
Теперь рассмотрим различные типы треугольников. Односторонний треугольник имеет одну из сторон больше или меньше других двух. Равнобедренный треугольник имеет две равные стороны и два равных угла. Равносторонний треугольник имеет все стороны и углы равными. Прямоугольный треугольник имеет один прямой угол, равный 90 градусам. Остроугольный треугольник имеет три острых угла, меньших 90 градусов. Тупоугольный треугольник имеет один угол больше 90 градусов.
| Тип треугольника | Описание |
|---|---|
| Односторонний треугольник | Имеет одну сторону, которая больше или меньше других двух. |
| Равнобедренный треугольник | Имеет две равные стороны и два равных угла. |
| Равносторонний треугольник | Имеет все стороны и углы равными. |
| Прямоугольный треугольник | Имеет один прямой угол, равный 90 градусам. |
| Остроугольный треугольник | Имеет три острых угла, меньших 90 градусов. |
| Тупоугольный треугольник | Имеет один угол больше 90 градусов. |
Вопрос-ответ

Какое основное определение луча в геометрии для 7 класса?
Луч в геометрии - это отрезок прямой, имеющий одно начало и бесконечное продолжение в одном направлении.
Какие свойства лучей в геометрии 7 класса?
Свойства лучей в геометрии 7 класса включают: у каждого луча есть начало и направление, они могут быть равными или параллельными, они могут пересекаться или быть противоположными.
Как определить положение луча относительно других объектов в геометрии 7 класса?
Положение луча относительно других объектов в геометрии 7 класса можно определить с помощью понятий пересечения, параллельности и сравнения углов. Например, луч может пересекать другой луч, быть параллельным или образовывать определенные углы с другими лучами.
Какие основные формулы связаны с лучами в геометрии 7 класса?
В геометрии 7 класса нет конкретных формул, связанных именно с лучами. Однако, при решении задач на геометрию, могут быть использованы формулы для вычисления длин отрезков, нахождения площадей фигур и другие общие формулы, которые могут быть применены и к лучам.



