Наша реальность, и в особенности разнообразные физические явления, неразрывно связаны с движением. Все, что нас окружает, вечно в движении. Одной из самых увлекательных форм движения является метаморфоза, при которой тело движется по криволинейной, закругленной траектории.
Мы глядим вокруг себя и видим, как все, начиная от планет нашей солнечной системы и заканчивая человеком, обретает жизнь, приобретает размеры и полеты в своем неповторимом танце вокруг опережающих и опаздывающих в своем бесконечном притяжении и отталкивании. Оказывается, сила определяет траекторию движения.
Будь то пули пушки или лебедь на озере, движение по криволинейной, закругленной траектории в физике обладает некими особыми свойствами. Во-первых, это постоянное изменение скорости вдоль пути, позволяющее телу преодолевать равномерное однородное движение. Во-вторых, это центростремительная сила, действующая на тело и удерживающая его на окружности. Также, чтобы изучить это явление, нужно рассмотреть ускорение, перпендикулярное скорости и направленное к центру. Исследование таких движений дает нам возможность глубже понять принципы работы вселенной и разгадать ее хитрости.
Основные понятия и термины
В данном разделе мы представляем основные понятия и определения, охватывающие тему движения по окружности в физике. Здесь рассматриваются базовые термины, необходимые для понимания и изучения физических процессов, связанных с движением по кривой линии, которая имеет форму замкнутого круга или окружности. Мы охватываем основные принципы и свойства, связанные с этим видом движения, используя разнообразные синонимы и вариации терминов.
| Термин | Определение |
|---|---|
| Радиус | Расстояние от центра окружности до любой ее точки |
| Центростремительное ускорение | Ускорение, направленное к центру окружности и возникающее при движении по окружности |
| Период | Время, за которое точка на окружности проходит полный оборот |
| Угловая скорость | Скорость, с которой точка на окружности меняет свое положение относительно центра окружности |
| Тангенциальная скорость | Скорость, направленная вдоль касательной к окружности |
| Круговая частота | Количество полных оборотов точки на окружности за единицу времени |
| Центростремительное ускорение | Ускорение, направленное к центру окружности и возникающее при движении по окружности |
Эти основные понятия играют важную роль в понимании физических явлений, связанных с движением по окружности. Они позволяют анализировать и описывать движение тел вращения, а также предсказывать и объяснять различные свойства и поведение систем, основанных на этом движении. Понимание этих понятий является фундаментом для более сложных концепций и теорий в физике.
Принцип инерции: неизменность направления скорости в движении по окружности
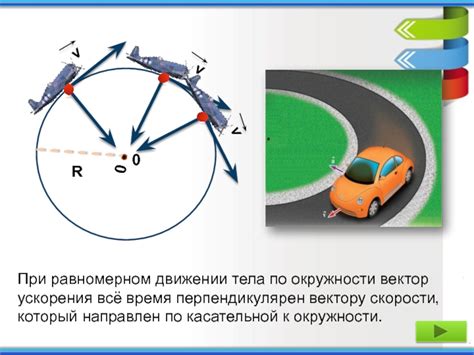
В физике существует основной принцип, называемый принципом инерции. Этот принцип утверждает, что тело, находящееся в равномерном движении, будет продолжать двигаться прямолинейно и со скоростью, пока на него не будет действовать внешняя сила.
Когда тело движется по окружности, оно необходимо постоянно изменять направление своей скорости. Из принципа инерции следует, что в отсутствие внешних сил на тело, оно будет сохранять свою скорость и направление движения вдоль окружности.
Однако, если на тело действует внешняя сила, оно будет отклоняться от своей натуральной траектории и изменять направление движения. Таким образом, в движении по окружности принцип инерции позволяет понять, почему тело будет двигаться радиально в результате воздействия внешних сил.
Принцип инерции в движении по окружности также связан с понятием центростремительной силы. Центростремительная сила придает телу направленное радиальное ускорение и обеспечивает его движение по окружности.
Центробежное ускорение и его особенности
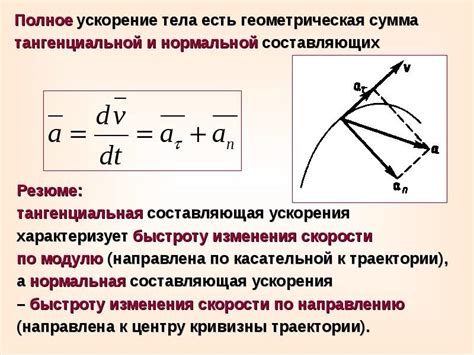
В данном разделе рассмотрим явление, связанное с перемещением тела по заданной траектории, обладающей формой окружности. Обратим внимание на специфический вид ускорения, который возникает при таком типе движения и имеет название центростремительного ускорения.
Центростремительное ускорение представляет собой векторную величину, направленную от тела к центру окружности, и характеризующую его изменение скорости. Основным свойством этого ускорения является то, что оно всегда направлено к центру окружности, поэтому его векторное значение отличается от направления самого движения тела.
Одной из важных характеристик центростремительного ускорения является его зависимость от радиуса окружности и скорости перемещения тела. Увеличение радиуса окружности или увеличение скорости движения приводит к возрастанию центростремительного ускорения. Это становится явным при рассмотрении уравнения, описывающего данное ускорение, которое пропорционально как скорости, так и радиусу окружности.
Центростремительное ускорение также является причиной изменения направления движения тела по окружности. Благодаря ему тело постоянно смещается по кривой траектории, сохраняя связь с ее центром. Данная особенность центробежного ускорения позволяет объяснить многие физические явления, такие как силы инерции при повороте на машине или движение спутников по орбитам вокруг планеты.
- Центростремительное ускорение всегда направлено от тела к центру окружности
- Размер центростремительного ускорения зависит от радиуса окружности и скорости перемещения тела
- Центростремительное ускорение является причиной изменения направления движения по окружности
- Центробежное ускорение играет важную роль в объяснении ряда физических явлений
Исключительные ситуации при движении вдоль окружности
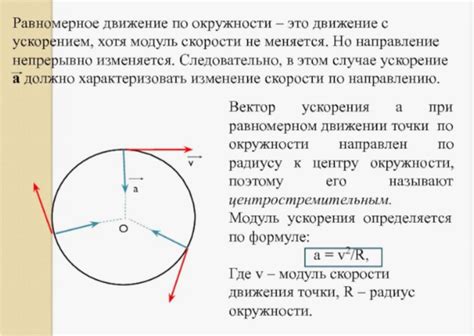
Кроме классического движения по окружности, в физике существуют граничные случаи, которые отличаются от обычной ситуации. В этих случаях принципы и свойства движения нарушаются или приобретают особые характеристики.
Измененная скорость. Одной из граничных ситуаций является движение с неустановившейся скоростью, когда она не является постоянной величиной. В этом случае, скорость объекта, движущегося вдоль окружности, может изменяться со временем. Она может увеличиваться или уменьшаться, что влияет на динамику движения и требует дополнительных учетов и анализа.
Непостоянное ускорение. Другим интересным граничным случаем является движение с изменяющимся ускорением. В обычной ситуации ускорение является постоянной величиной, но иногда возникают ситуации, когда оно меняется в процессе движения. В таких случаях, направление или величина ускорения могут претерпевать изменения, что вносит существенные изменения в поведение объекта на окружности.
Эффекты искажений. Некоторые граничные ситуации связаны с появлением искажений, которые изменяют форму окружности или ее радиус. Например, объект может двигаться вдоль эллипса, что приводит к нестандартному поведению и множеству интересных эффектов. Также возможно смещение центра окружности, что приводит к изменению осей и неоднородному движению.
Граничные случаи движения по окружности представляют собой интересную область исследования в физике. Изучение этих случаев позволяет лучше понять и описать различные аспекты движения, а также обнаружить новые явления и закономерности.
Законы сохранения и движение по окружности

Этот раздел посвящен законам сохранения, которые играют важную роль в изучении движения объектов по окружности. У этих законов есть свои особенности и свойства, которые помогают понять и объяснить различные аспекты движения.
Закон сохранения энергии является ключевым понятием при изучении движения по окружности. Он утверждает, что в закрытой системе энергия сохраняется, то есть не создается и не уничтожается, а только преобразуется из одной формы в другую. В контексте движения по окружности, закон сохранения энергии позволяет анализировать изменение кинетической и потенциальной энергии, а также выявить зависимости между ними.
Закон сохранения момента импульса также играет важную роль при рассмотрении движения по окружности. Он утверждает, что если на объект, движущийся по окружности, не действуют внешние моменты сил, то момент импульса этого объекта остается постоянным. Это означает, что при изменении радиуса или скорости движения объекта по окружности, его момент импульса остается неизменным.
Законы сохранения позволяют предсказать и объяснить особенности движения по окружности, а также связать различные величины, такие как энергия, момент импульса и скорость. Изучение и применение этих законов позволяют описать и понять разнообразные явления и процессы, связанные с движением по окружности в физике.
Расчеты и примеры траектории движения по кривой линии
В этом разделе мы рассмотрим основные методы и приемы расчета движения тела по криволинейной траектории. Здесь вы сможете ознакомиться с конкретными примерами и узнать, как можно определить параметры движения, такие как скорость, ускорение и силы, действующие на тело в процессе его движения вдоль кривой линии.
Траектория движения – это закономерность изменения положения тела в пространстве с течением времени. Такая закономерность может быть представлена в виде кривой линии, отображающей маршрут движения тела.
Для расчета движения по криволинейной траектории необходимо знание основных физических величин и законов, связанных с движением тела. Это позволяет определить, какие силы действуют на тело и как изменяются его скорость и ускорение в процессе движения по данной траектории.
Примеры расчетов движения по окружности позволят наглядно проиллюстрировать применение теоретических знаний в практической задаче. Мы рассмотрим случаи равномерного движения по окружности, а также движения с постоянным угловым ускорением. В каждом примере будут представлены формулы расчета скорости, ускорения и силы, а также будет показано, как испытываемая телом сила влияет на его движение.
Применение кругового движения в технических и научных областях

Выборочная искусственная имитация движения точки по окружности, применяемая в различных практических исследованиях и технических задачах, предлагает возможность решать множество проблем, связанных с передвижением и вращением. Круговое движение находит применение в различных областях, таких как механика, электроника, астрономия, медицина и другие.
В инженерии и технике круговое движение применяется для создания и оптимизации механизмов и систем, позволяющих осуществлять разные виды работы, начиная от простых вентиляторов и двигателей, и до сложных роботизированных систем и промышленных машин. Исследование и практическое использование движения по окружности позволяет достичь высокой точности, стабильности и эффективности в механических процессах.
В научных исследованиях движение по окружности играет значительную роль при изучении физических явлений и характеристик материалов. Это движение позволяет проводить такие эксперименты, которые невозможно было бы осуществить с прямолинейным движением. Например, при масс-спектрометрии, орбитальных экспериментах в астрономии или моделировании движения электронов в атоме.
В медицине круговое движение находит применение в ряде процедур и диагностических методов. Например, круглый обход мускулов на терапевтическом массаже, окружность крови внутри сердца при эхокардиографии или движение колеблющейся частички при проведении ультразвуковой терапии.
Вопрос-ответ

Как определить, движется ли объект по окружности или нет?
Для определения движения по окружности необходимо проверить, сохраняется ли радиус и угловая скорость объекта на протяжении времени. Если радиус и угловая скорость остаются постоянными, то объект движется по окружности.
Каковы принципы движения по окружности в физике?
Принципы движения по окружности в физике основываются на законах сохранения момента импульса и момента силы. Когда объект движется по окружности, момент силы равен нулю, а момент импульса постоянен.
Какие свойства движения по окружности важны для физики?
Важными свойствами движения по окружности являются постоянство радиуса и угловой скорости, центростремительное ускорение, которое направлено к центру окружности, и периодическое изменение кинетической и потенциальной энергии объекта.
Как определить периодическое изменение кинетической и потенциальной энергии объекта, движущегося по окружности?
Для определения периодического изменения кинетической и потенциальной энергии объекта на окружности необходимо учесть, что кинетическая энергия максимальна, когда потенциальная энергия минимальна и наоборот. Участвующая здесь формула: E = K + П, где E - полная механическая энергия, K - кинетическая энергия, П - потенциальная энергия.
Может ли объект двигаться по окружности с постоянной скоростью?
Нет, объект не может двигаться по окружности с постоянной скоростью. Движение по окружности подразумевает изменение направления скорости, что означает изменение вектора скорости. При постоянной скорости вектор скорости остается неизменным, что не совместимо с движением по окружности.



