Успешное обучение математике начинается с изучения основных понятий, которые лежат в основе различных математических операций. В одноименном разделе предлагается познакомиться с одной из таких важных концепций, которая начинает свое знакомство с учениками именно в шестом классе.
В процессе изучения математики, ученики встречаются с различными терминами и определениями, включая нод нок, которые являются ключевыми элементами для умения выполнять арифметические операции. Благодаря этим понятиям школьники учатся проводить самостоятельные расчеты и выполнять сложные математические примеры.
Цель данной статьи - изучение темы "нод нок" в математике с помощью конкретных примеров и разъяснений. Во время прохождения материала, каждый ученик сможет получить полное понимание сути этих понятий и научиться применять их в многочисленных заданиях и задачах по математике.
Значение "Общий делитель" и "Минимальное общее кратное"
Когда мы говорим о двух числах, несомненно, важно знать, каким образом их можно связать друг с другом. Для этого существуют такие понятия, как "Общий делитель" и "Минимальное общее кратное".
Общий делитель - это число, которое может нацело делить одновременно два или более числа. Другими словами, это число, которое является общим для всех чисел, которые мы рассматриваем. Общие делители есть у любых чисел, однако важно найти их наименьшее значение.
Примером общего делителя может служить число, которое одновременно делится на 4 и на 6.
Минимальное общее кратное, в свою очередь, представляет собой наименьшее возможное число, которое делится нацело на все числа, которые мы рассматриваем. Он позволяет определить такую характеристику, которая будет общей для этих чисел.
Давайте представим, что нам нужно найти наименьшее число, которое делится на 2, 3 и 5. В этом случае минимальное общее кратное будет собой число, которое делится нацело на все эти три числа.
Таким образом, понимание определений "Общий делитель" и "Минимальное общее кратное" позволяет нам определить связь между различными числами и проводить соответствующие вычисления.
Примеры применения наибольшего общего делителя и наименьшего общего кратного

В диапазоне шестых классов математики, существует несколько увлекательных примеров, демонстрирующих использование наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) в различных ситуациях. Эти числовые концепции играют ключевую роль в решении различных задач, связанных с математическими отношениями и измерением. Давайте рассмотрим несколько интересных примеров, чтобы лучше понять, как НОД и НОК помогают нам в решении разнообразных задач и упрощении вычислений.
Пример 1: Разделение яблок
Представьте, что у вас есть 24 яблока и вы хотите разделить их между своими друзьями так, чтобы каждому досталось одинаковое количество яблок. Чтобы найти наибольшее количество друзей, которым вы можете поделить эти яблоки равномерно, вы должны найти НОД чисел 24 и количества ваших друзей.
(продолжение в стиле предыдущего абзаца)
Нахождение наибольшего общего делителя и наименьшего общего кратного чисел

Наибольший общий делитель (НОД) - это наибольшее число, которое одновременно является делителем для всех данных чисел. Он помогает нам определить, какие числа являются общими делителями для заданных чисел и какие числа являются их наибольшим общим делителем.
Наименьшее общее кратное (НОК) - это минимальное число, которое кратно всем заданным числам. Оно позволяет нам определить, какие числа являются кратными для всех данных чисел и какое число является их наименьшим общим кратным.
Для нахождения НОД и НОК чисел существуют специальные алгоритмы и методы. Один из таких методов - это разложение чисел на простые множители и последующее определение общих множителей и их степеней для НОД, а также определение общих множителей и их степеней с наибольшими значениями для НОК.
Таким образом, нахождение НОД и НОК чисел позволяет нам находить связи между числами, решать задачи на делимость и кратность, а также проводить различные математические операции с числами.
Основные свойства высшей общей кратности и наименьшего общего кратного

Высшая общая кратность двух чисел - это наибольшее число, которое является делителем обоих данных чисел. Она позволяет определить, какое минимальное число надо выбрать, чтобы оно делилось без остатка на оба числа.
Наименьшее общее кратное двух чисел - это наименьшее число, которое делится без остатка на оба данных числа. Оно позволяет определить, какое минимальное число необходимо выбрать, чтобы оно было кратным обоим числам.
Нахождение высшей общей кратности и наименьшего общего кратного помогает при решении различных задач, связанных с дробями, пропорциями и упрощением выражений. Благодаря этим свойствам, мы можем оперировать числами и получать правильные результаты.
Знание этих основных свойств позволяет решать разнообразные задачи, связанные с числами, и использовать их в повседневной жизни для расчетов и анализа данных.
Применение наибольшего общего делителя и наименьшего общего кратного в задачах, связанных с долями

В долевых задачах, возникающих в различных сферах нашей жизни, для решения часто требуется нахождение наибольшего общего делителя и наименьшего общего кратного. Наибольший общий делитель (НОД) помогает найти наибольшую общую часть долей, в то время как наименьшее общее кратное (НОК) определяет наименьшую общую единицу измерения долей.
Пример: Представим себе ситуацию, где необходимо разделить торт между несколькими людьми. Каждый человек хочет получить долю торта, состоящую из одинакового количества кусочков. Чтобы достичь равномерного разделения, необходимо найти НОД количества кусочков, которые хотят каждый получить участники. Затем НОК даст нам наименьшее количество кусочков, которое нужно разделить на равные доли для удовлетворения всех участников.
Таким образом, применение НОД и НОК в задачах на доли позволяет находить решения, обеспечивающие равномерное и справедливое деление между участниками.
Решение задач на кратность с использованием НОД и НОК

Одной из наиболее распространенных проблем, связанных с кратностью чисел, является определение общей кратности двух или более чисел. Для этого мы можем использовать понятие НОК. НОК двух чисел - это наименьшее число, которое делится на оба числа без остатка. Путем вычисления НОК мы можем определить, через какое промежуток времени два события произойдут одновременно или когда два агента снова будут находиться на одной точке.
Кроме того, НОК также помогает в решении задач на кратность, связанных с расчетами и планированием. Например, если мы знаем, что один автобус отправляется через 10 минут, а другой - через 15 минут, мы можем использовать НОК для определения, сколько минут пройдет до следующего одновременного отбытия обоих автобусов.
НОД, с другой стороны, помогает нам определить общие делители двух чисел. Он позволяет нам разбить задачу на более мелкие подзадачи и найти общий фактор чисел.
| Пример задачи | Решение с использованием НОД и НОК |
|---|---|
| Найти наименьшее число, которое делится на 6, 8 и 10 без остатка. | Для решения данной задачи мы найдем НОК чисел 6, 8 и 10. НОК(6, 8, 10) = 120. Таким образом, наименьшее число, которое делится на 6, 8 и 10 без остатка, равно 120. |
| Определить, через сколько минут колесо обозрения и большой часовой механизм оказываются в начальном положении. | Мы найдем НОК периодов вращения колеса обозрения и большого часового механизма. Затем мы узнаем, через какое время они окажутся снова в одной точке. |
Практические задания с вычислением наибольшего общего делителя и наименьшего общего кратного

В данном разделе мы рассмотрим несколько интересных задач, в которых понадобятся навыки вычисления наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК). Такие задачи широко применяются как в математике, так и в повседневной жизни, например, для решения задач по распределению предметов или времени.
Давайте рассмотрим первое задание. У нас есть четыре друзей, у каждого из которых есть несколько яблок. Наша задача - распределить яблоки так, чтобы в каждой группе было одинаковое количество яблок. Для этого нам понадобится вычислить НОД количества яблок у каждого друга. Наибольший общий делитель позволит нам узнать, сколько яблок нужно каждому другу, чтобы они были равноправными в этом аспекте.
Перейдем ко второму заданию. Допустим, у нас есть два объекта, которые совершают колебания. Один объект колеблется каждые 8 секунд, а второй - каждые 12 секунд. Нам нужно найти момент времени, когда эти два объекта будут колебаться вместе. Для этого вычислим НОК периодов колебаний каждого объекта. Наименьшее общее кратное позволит нам определить, через сколько секунд объекты будут совершать колебания одновременно.
Таким образом, вычисление НОД и НОК имеет практическое значение в задачах, связанных с равномерным распределением ресурсов или событий. Умение применять эти концепции в реальной жизни помогает решить множество задач эффективно и точно.
Использование наименьшего общего делителя и наименьшего общего кратного в разложении чисел на простые множители

Наименьший общий делитель - это наименьшее число, на которое можно без остатка разделить два или более числа. Он помогает нам найти общие простые множители у разных чисел и сократить их до наименьшего возможного значения.
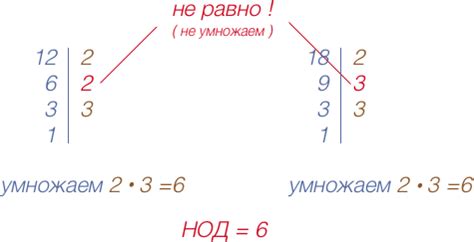
Пример: Разложим числа 12 и 18 на простые множители. Найдем их НОД:
12 = 2 * 2 * 3
18 = 2 * 3 * 3
НОД(12, 18) = 2 * 3 = 6
Наименьшее общее кратное - это наименьшее число, которое делится без остатка на два или более числа. Он помогает нам найти общие простые множители у разных чисел и увеличить их до наименьшего возможного значения.
Пример: Разложим числа 6 и 8 на простые множители. Найдем их НОК:
6 = 2 * 3
8 = 2 * 2 * 2
НОК(6, 8) = 2 * 2 * 2 * 3 = 24
Использование наименьшего общего делителя и наименьшего общего кратного значительно упрощает разложение чисел на множители, позволяя найти наименьшее и наибольшее возможное значение для каждого из них. Это может быть полезно, например, при решении задач на поиск наименьшего общего кратного нескольких чисел или при факторизации числа.
Ступеньки к математическому мастерству: тренируемся на задачах с расчетами НОД и НОК

В этом разделе представлены задачи, которые помогут вам развить навыки работы с понятиями НОД и НОК, этих универсальных математических инструментов. Мы предлагаем вам потренироваться в решении интересных и разнообразных задач, где пригодятся знания о наибольшем общем делителе и наименьшем общем кратном чисел.
Во время решения каждой задачи вам придется активно применять ваш математический аппарат, анализировать условия и выбирать подходящие стратегии. Решение задач требует логического мышления, творческого подхода и навыков работы с числами.
Разнообразие задач, представленных в этом разделе, позволит вам познакомиться с различными ситуациями, где расчеты НОД и НОК играют важную роль. Вы будете решать задачи на разные предметы, такие как делящиеся на цифры числа, доли, время и расписание, справедливость различных условий и многое другое.
Тренировка на этих задачах поможет вам развить ваше математическое мышление, повысить навыки работы с числами и научиться применять полученные знания в реальных ситуациях. Уверены, что успешное выполнение задач принесет удовлетворение и поможет вам стать более навыкатным математиком!
Вопрос-ответ

Что такое нод нок в математике?
Нод нок (наибольший общий делитель и наименьшее общее кратное) - это два понятия, которые используются в математике для работы с дробями и целыми числами. Нод нок позволяют нам находить общие свойства и связи между разными числами. Нод нок двух чисел - это наибольшее число, на которое оба числа делятся без остатка, а нок двух чисел - это наименьшее число, которое делится на оба числа без остатка.
Как можно рассчитать нод нок двух чисел?
Нод двух чисел можно рассчитать с помощью алгоритма Евклида. Для этого необходимо поделить большее число на меньшее и запомнить остаток. Затем это остаток нужно поделить на предыдущий остаток, и так далее, пока не получим остаток равный нулю. Нодом является последнее ненулевое число. Нок двух чисел можно рассчитать, зная их нод, по формуле: нок = (число1 * число2) / нод.
Можете привести примеры использования нод нок в математике?
Конечно! Один из примеров использования нод нок - это упрощение дробей. Для этого необходимо найти нод числителя и знаменателя дроби, а затем разделить оба числа на этот нод. Например, дробь 4/8 можно упростить, найдя нод чисел 4 и 8, который равен 4. Поделив числитель и знаменатель на 4, получим упрощенную дробь 1/2. Еще один пример использования нод нок - это нахождение общего времени выполнения двух действий. Если первое действие повторяется через каждые 4 часа, а второе - через каждые 6 часов, то общее время выполнения обоих действий будет равно их ноку, то есть 12 часам.



