Существует удивительный способ доказать равенство нулю определителей без привлечения вычислений. Этот метод позволяет обнаружить, что значение определителя равно нулю, просто путем внимательного изучения свойств матрицы. Для достижения этой цели не требуется сложных вычислений или экспертных навыков в математике. Уникальность данного подхода заключается в его интуитивной и элегантной сути.
Итак, как реализовать этот метод и оправдать равенство нулю определителей? Ответ прост: мы будем исследовать подмножество известных свойств матрицы, чтобы выявить скрытые взаимосвязи. Такой подход открывает возможность увидеть глубинные механизмы, лежащие в основе определителей, и их связь с нулевым значением.
Замечательно то, что данная методика доступна всем, независимо от уровня математической подготовки. Она ориентирована на любознательных исследователей, которые желают прикоснуться к величайшим открытиям математического мира. Следуя нашим рекомендациям и используя данную методику, вы сможете увидеть красоту и сложность математических объектов через простоту и интеллектуальную логику.
Использование теоремы о ранге матрицы для подтверждения нулевого значения определителя

Определитель матрицы является важной характеристикой, которая отображает базисность системы векторов, записанных в столбцы этой матрицы. Если определитель равен нулю, то система векторов является линейно зависимой, и можно утверждать, что они лежат в одной плоскости или совпадают. Нашей задачей будет доказать это утверждение без явных вычислений определителя.
Для этого мы воспользуемся теоремой о ранге матрицы, которая утверждает, что ранг матрицы равен максимальному числу линейно независимых строк (или столбцов), которые могут быть выделены в этой матрице. Используя это свойство, мы покажем, что приравнивание определителя к нулю эквивалентно тому, что количество линейно независимых строк (или столбцов) матрицы меньше чем размерность матрицы.
| Строка 1 | Строка 2 | Строка 3 | |
| Столбец 1 | x | x | x |
| Столбец 2 | y | y | y |
| Столбец 3 | z | z | z |
Чтобы убедиться в этом, рассмотрим пример выше: трехнарная матрица, в которой все элементы в одной строке (или столбце) равны между собой. Если мы обратим внимание, то сразу заметим, что строки (или столбцы) этой матрицы линейно зависимы, так как существует возможность выразить одну строку (или столбец) через другие. Следовательно, ранг такой матрицы будет меньше размерности, а определитель будет равен нулю.
Таким образом, использование теоремы о ранге матрицы позволяет нам доказать равенство нулю определителя без необходимости проводить вычисления. Этот подход является эффективным и может применяться в различных задачах, связанных с линейной алгеброй и матричными вычислениями.
Сущность и свойства определителя матрицы

Определитель – это числовое значение, вычисляемое на основе элементов матрицы. Он является своеобразной мерой для определенных геометрических и алгебраических свойств матрицы. Своеобразность определителя заключается в его роли при описании изменений объема, расстояния и ориентации линейных преобразований. Он также может быть использован для решения систем линейных уравнений и нахождения обратной матрицы.
Одно из свойств определителя – это его связь с вычислительными операциями над матрицами. Изменение порядка строк или столбцов матрицы приводит к изменению знака определителя, но его абсолютное значение остается неизменным. Это позволяет упростить вычисления и получить эквивалентные записи определителей с использованием теории перестановок. Также можно выделить свойства определителя, которые позволяют заменить некоторые строки или столбцы на их линейные комбинации без изменения значения определителя. Это упрощает анализ системы линейных уравнений и позволяет находить определитель, избегая прямого вычисления.
Теорема о ранге матрицы и связь с детерминантом

Основная идея теоремы состоит в том, что если матрица имеет нулевой определитель, то ее ранг не может быть максимальным, и, следовательно, в ней обязательно существует линейно зависимая система столбцов. Это доказывает связь между определителем и рангом матрицы, позволяя нам утверждать, что нулевой определитель означает наличие линейно зависимых столбцов. Такое равенство может быть полезным в различных математических и инженерных задачах.
Представление матрицы в виде блочной структуры

В данном разделе рассматривается метод представления матрицы в виде блочной структуры, что позволяет более наглядно и систематично организовать данные. Блочная структура позволяет разделить матрицу на составные части или блоки, которые могут быть упорядочены и организованы по определенным правилам.
Распределение элементов матрицы в блочной структуре может быть осуществлено различными способами. Например, матрица может быть разделена на равные квадратные блоки, которые могут быть дальше сгруппированы в регулярные подматрицы. Другой вариант может предусматривать разбиение матрицы на блоки различных размеров в зависимости от специфических свойств элементов или требований задачи.
Такой подход позволяет более эффективно проводить анализ и манипуляции с матрицей. Каждый блок может иметь свою структуру и порядок элементов, что способствует пониманию взаимосвязи между элементами и их взаимодействию. Кроме того, блочная структура может значительно упростить проведение операций над матрицами, таких как сложение, умножение и нахождение определителя.
Использование блочной структуры матрицы может быть особенно полезным при решении сложных задач линейной алгебры, в том числе при доказательстве равенства нулю определителей. Анализирование подматриц внутри блоков может помочь выявить закономерности и свойства, которые могут привести к доказательству равенства нулю определителей без проведения вычислений.
Понятие элементарных преобразований и их воздействие на определитель

Есть несколько важных факторов, которые следует учитывать при применении элементарных преобразований. Во-первых, определитель матрицы остается неизменным при выполнении элементарных преобразований. Это означает, что, несмотря на изменения в матрице, определитель остается постоянным. Во-вторых, элементарные преобразования позволяют использовать свойства определителя для упрощения вычислений. Например, применение элементарных преобразований может привести к матрице с простой структурой, в которой обнаруживаются явные закономерности, с помощью которых можно легче вычислить определитель.
Для лучшего понимания важности элементарных преобразований и их воздействия на определитель матрицы, рассмотрим несколько примеров. Применение элементарных преобразований может привести к упрощению матрицы, позволяя нам применить свойство комплексного алгебраического вычисления к определителю, такие как "смена знака при перестановке строк" или "разложение по строке". Это упрощает процесс вычисления определителя и позволяет получить точный результат.
Соответствие между рангом матрицы и количеством ее ненулевых миноров

В данном разделе рассматривается важное свойство матриц, которое связывает их ранг и количество ненулевых миноров. Ранг матрицы определяется, как максимальное количество линейно независимых строк или столбцов, в то время как ненулевые миноры представляют собой подматрицы, определитель которых не равен нулю.
- Вначале рассмотрим матрицу, у которой все строки или столбцы являются линейно зависимыми.
- В такой матрице любой из ее миноров будет равен нулю, так как существует нетривиальная линейная комбинация строк или столбцов, дающая ноль.
- Следовательно, количество ее ненулевых миноров будет равно нулю, что соответствует ее рангу.
- Теперь рассмотрим матрицу, у которой строки или столбцы являются линейно независимыми.
- В такой матрице существует хотя бы один ненулевой минор, так как определитель подматрицы, составленной из линейно независимых строк или столбцов, будет не нулевым.
- Количество ненулевых миноров в такой матрице будет равно ее рангу, так как каждый ненулевой минор будет определителем подматрицы, составленной из линейно независимых строк или столбцов.
Таким образом, мы доказали, что если все строки или столбцы матрицы линейно зависимы, то количество ее ненулевых миноров равно нулю. Если же строки или столбцы матрицы линейно независимы, то количество ее ненулевых миноров равно ее рангу. Это важное соответствие помогает в понимании связи между рангом матрицы и ее ненулевыми минорами в рамках линейной алгебры.
Достижение равенства нулю определителя в случае матрицы нулевого ранга
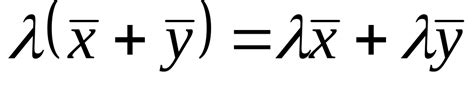
Результатом будет убедительное доказательство равенства нулю определителя при нулевом ранге матрицы, в котором мы запрограммируем наш мозг на поиск альтернативных путей понимания и убеждения в этом факте, не прибегая к скучным расчетам и вычислениям значений элементов матрицы.
Примеры применения теоремы о ранге матрицы для подтверждения нулевого значения определителей

В первом примере рассмотрим квадратную матрицу, у которой все строки являются линейными комбинациями некоторых других строк. Используя теорему о ранге матрицы, мы можем показать, что ранг данной матрицы равен числу её независимых строк, что в данном случае является нулем. Следовательно, определитель такой матрицы будет равен нулю.
| a | b | c |
| 2a | 2b | 2c |
| 3a | 3b | 3c |
Во втором примере рассмотрим матрицу, которая содержит строки или столбцы, являющиеся линейной комбинацией других строк или столбцов. Используя теорему о ранге матрицы, мы можем установить, что ранг данной матрицы будет меньше, чем её размерность. Это означает, что все миноры матрицы будут равны нулю, что в свою очередь приводит к нулевому значению определителя.
| a+b | 2a+2b | c |
| a | 2a | c |
| (a+b)+(a) | (2a+2b)+(2a) | c+c |
Таким образом, данные примеры наглядно иллюстрируют применение теоремы о ранге матрицы для доказательства равенства нулю определителей, позволяя избежать вычислений и основываясь на линейной зависимости строк или столбцов матрицы.
Важность практического применения результатов
Применение в алгебраической геометрии
В алгебраической геометрии изучается связь между алгебраическими уравнениями и геометрическими объектами, что позволяет решать сложные геометрические задачи с использованием алгебраических методов. Знание о равенстве нулю определителей является необходимым инструментом для исследования свойств и формулирования алгоритмов решения таких задач.
Применение в теории вероятностей
Применение в математической физике
В математической физике изучаются математические модели, описывающие физические явления. При решении уравнений, связанных с такими моделями, равенство нулю определителей может быть использовано для получения упрощенных аналитических решений или численного моделирования физических процессов.
Вопрос-ответ

Каким образом можно доказать равенство нулю определителей без проведения вычислений?
В математике существуют специальные свойства и теоремы, которые позволяют доказать равенство нулю определителей без выполнения вычислений. Одним из таких методов является использование свойства линейной зависимости строк или столбцов матрицы. Если строки или столбцы матрицы являются линейно зависимыми, то определитель этой матрицы равен нулю. Это можно легко проверить с помощью элементарных преобразований, например, если одна строка матрицы является линейной комбинацией других строк.
Можно ли доказать равенство нулю определителей с использованием свойств диагональных матриц?
Да, можно. Если рассматривать диагональную матрицу, то ее определитель равен произведению элементов на главной диагонали. Если хотя бы один из элементов на главной диагонали равен нулю, то определитель такой матрицы будет равен нулю. Таким образом, доказать равенство нулю определителей можно, показав, что в матрице присутствует хотя бы один нулевой элемент на главной диагонали.
Каким образом можно использовать свойства преобразований строк и столбцов для доказательства равенства нулю определителей?
Для доказательства равенства нулю определителей можно использовать свойства элементарных преобразований строк и столбцов. Например, если в матрице существует строка или столбец, являющийся линейной комбинацией других строк или столбцов, то определитель этой матрицы будет равен нулю. Это можно проверить, выполнив соответствующие преобразования, например, вычтя из одной строки матрицы другую строку, умноженную на некоторое число.



