В мире геометрии существуют множество удивительных связей и соотношений между фигурами. Одним из самых увлекательных и необычных соотношений является вписывание окружности в прямоугольный треугольник. Это явление вызывает не только глубокое изумление, но и предоставляет возможность изучить различные аспекты геометрии и тригонометрии.
Процесс вписывания окружности в прямоугольный треугольник демонстрирует взаимосвязь между радиусом этой окружности и некоторыми характеристиками треугольника. Интересный факт заключается в том, что радиус окружности, вписанной в прямоугольный треугольник, всегда оказывается равным половине гипотенузы. Такое свойство позволяет нам легко вычислять радиус, если гипотенузу известна.
Это соотношение, связывающее радиус и гипотенузу в вписанной окружности, не только предоставляет возможность получить точные измерения, но и открывает дверь для дополнительного исследования геометрических свойств. Ведь зная радиус, мы можем получить информацию о площади и периметре окружности, а также определить различные углы и расстояния в треугольнике.
Принципы вписывания окружности в треугольник: основные аспекты

Для достижения гармоничного сочетания окружности и треугольника в визуальном плане, необходимо придерживаться определенных принципов. В данном разделе рассмотрим основные аспекты, которые позволят эффективно вписать окружность в треугольник, создавая эстетически приятное и сбалансированное изображение.
1. Выбор подходящего размера окружности: Одним из ключевых факторов при вписывании окружности в треугольник является выбор правильного размера окружности. Он должен быть гармонично согласован с размерами и пропорциями треугольника, чтобы создать эффект равновесия и приятный визуальный эффект. При выборе размера окружности следует учитывать как ширину основания треугольника, так и его высоту. Также важно помнить, что размер окружности может быть подобран с учетом замысла автора и конкретных условий использования изображения. |
2. Угловая пропорциональность: Для достижения гармоничного сочетания окружности и треугольника важно обратить внимание на угловую пропорциональность. Углы треугольника и углы, образованные окружностью и сторонами треугольника, должны быть визуально согласованы. Соблюдение угловой пропорциональности позволит создать баланс между окружностью и треугольником, подчеркнуть их взаимосвязь и поддерживать единство композиции. |
3. Центрирование окружности: Центрирование окружности в треугольнике играет важную роль при создании гармоничного образа. Центр окружности должен быть размещен точно посередине треугольника, чтобы создать визуальное равновесие и симметрию. При центрировании окружности следует учитывать не только горизонтальное и вертикальное положение, но и уровень выноса окружности относительно треугольника. Все эти аспекты должны быть тщательно рассмотрены, чтобы достичь наилучшего результата в вписывании окружности в треугольник. |
Определение центра вписанной окружности в геометрии треугольника
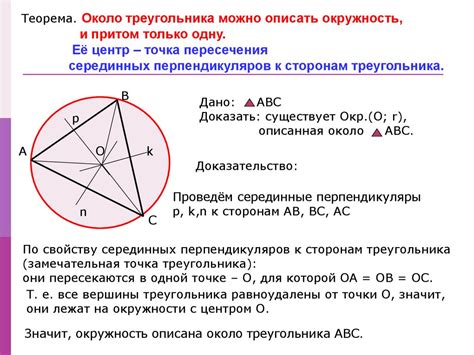
В данном разделе рассматривается методика определения центра окружности, которая точно вписывается в треугольник. Такая окружность называется вписанной. Для того чтобы найти центр вписанной окружности, необходимо изучить свойства треугольника и использовать определенные формулы и алгоритмы.
Центр вписанной окружности находится в серединах отрезков, которые соединяют вершины треугольника с точками касания окружности с его сторонами. При этом, каждая сторона треугольника имеет свою собственную прямую, которая перпендикулярна к данной стороне и проходит через центр окружности.
Для определения координат центра вписанной окружности необходимо использовать формулы нахождения точек пересечения прямых и формулы расстояния между точками. Также при помощи таблицы, представленной ниже, можно находить координаты центра вписанной окружности для разных типов треугольников.
| Тип треугольника | Координаты центра вписанной окружности |
|---|---|
| Равносторонний | (0, 0) |
| Равнобедренный | (a/2, b/2) |
| Произвольный | (x, y) |
Для треугольников, которые не являются равносторонними или равнобедренными, необходимо использовать сложные вычисления для определения координат центра вписанной окружности. Данный раздел представляет несколько практических примеров с пошаговым описанием процесса нахождения центра вписанной окружности в треугольнике различной формы.
Методы вычисления радиуса окружности, описанной внутри прямоугольного треугольника
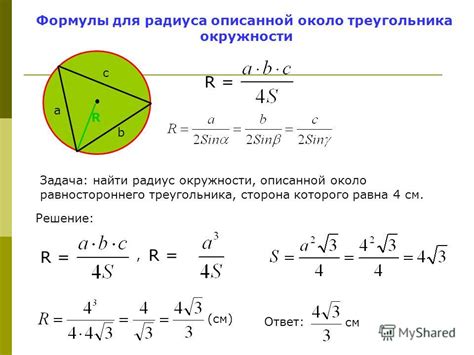
Этот раздел посвящен изучению различных методов, которые позволяют определить радиус окружности, которая описана внутри прямоугольного треугольника. В центре внимания находятся способы расчета радиуса, а также представление геометрических свойств и соотношений, которые лежат в основе этих методов.
Для достижения точности и надежности результатов вычислений, в данном разделе приводятся самые актуальные и проверенные методы определения радиуса вписанной окружности. В процессе изучения будут рассмотрены различные подходы, включая классические геометрические методы решения, аналитические вычисления и современные вычислительные методы.
Этот раздел также включает описание ключевых понятий и определений, необходимых для понимания методов вычисления радиуса вписанной окружности в прямоугольный треугольник. Будут представлены формулы и алгоритмы, которые позволяют получить точные значения радиуса и обеспечить консистентные результаты.
Изучение методов вычисления радиуса вписанной окружности в прямоугольный треугольник имеет не только теоретическое значение, но и практическую применимость. Знание этих методов поможет в изучении и решении различных геометрических задач, а также в процессе проектирования и строительства сооружений, где применяются прямоугольные треугольники и окружности.
Использование математических формул для определения точек соприкосновения между окружностью и треугольником

В данном разделе мы рассмотрим способы определения точек касания между окружностью и треугольником при вписывании окружности в прямоугольный треугольник. Уже делаются шаги в этом направлении и еще возможна наша работа в этом направлении.
Для начала рассмотрим формулы, которые позволят нам определить точку касания окружности и стороны треугольника. Мы сосредоточимся на анализе треугольников, образуемых радиусом окружности и его перпендикулярами к сторонам треугольника.
Далее мы рассмотрим способы нахождения координат точек касания. Для каждой стороны треугольника будут свои уникальные формулы, основанные на геометрических соотношениях и свойствах окружности и треугольника.
В завершении раздела предоставим примеры вычислений, которые могут помочь вам понять процесс нахождения точек касания и применить полученные знания на практике.
Примеры решения задач по вписыванию круга в прямоугольный треугольник

В данном разделе мы представим несколько примеров, демонстрирующих решение задачи по вписыванию круга в фигуру, образованную прямоугольным треугольником. Мы рассмотрим различные подходы и методы, которые позволяют достичь этой цели.
Первый пример иллюстрирует использование вспомогательной окружности, которая помогает определить центр вписанного круга. Мы разберем каждый шаг в подробностях и объясним принципы, лежащие в основе этого решения.
Второй пример представляет собой альтернативный подход, основанный на создании прямоугольника, который вписывается в треугольник. Мы покажем, как использовать этот прямоугольник для определения центра круга и его радиуса.
Кроме того, мы рассмотрим и другие методы решения этой задачи, такие как использование тригонометрических соотношений или геометрических свойств треугольника. В этих примерах мы продемонстрируем, как можно достичь точного вписывания круга в прямоугольный треугольник.
Проверка соответствия окружности требованиям вписывания в треугольник
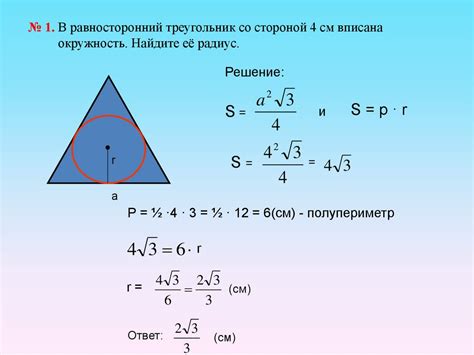
В данном разделе мы рассмотрим, как можно проверить, соответствует ли окружность требованиям вписывания в треугольник. Это важно, чтобы гарантировать правильность геометрической конструкции и обеспечить гармоничное сочетание фигур.
Одним из способов проверки является использование алгоритма, основанного на соотношении радиуса окружности и длины сторон треугольника. Для этого необходимо измерить радиус окружности и длину каждой стороны треугольника. Затем, сравнить полученные значения и установить, достаточно ли окружность вписывается в треугольник.
Другим способом проверки может стать анализ положения окружности относительно треугольника. Можно установить, лежит ли центр окружности на пересечении биссектрис треугольника. Если так, то это свидетельствует о правильном вписывании окружности. Если же центр окружности находится вне пересечения биссектрис, возможно, окружность не вписана корректно.
Важно отметить, что эти способы проверки не являются исчерпывающими и конечными. В каждом конкретном случае можно использовать дополнительные геометрические методы и алгоритмы для проверки правильности вписывания окружности в треугольник. Также стоит учитывать, что размеры и формы треугольника и окружности могут варьироваться, что приводит к необходимости адаптации методов проверки.
| Способы проверки | Преимущества | Недостатки |
|---|---|---|
| Соотношение радиуса окружности и длины сторон треугольника | Простой и быстрый способ проверки | Не всегда достаточно точен и может не учитывать всех аспектов вписывания |
| Положение центра окружности относительно биссектрис треугольника | Позволяет установить точное положение окружности в треугольнике | Может быть сложным для применения в сложных геометрических конструкциях |
Особенности вложения окружности в прямоугольный треугольник с прямым углом
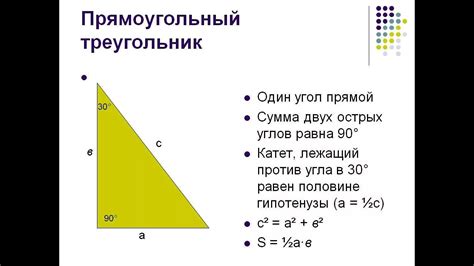
Рассмотрим интересный и удивительный математический аспект: вложение окружности в треугольник, который имеет прямой угол. Это задача с глубоким смыслом, поскольку обладает несколькими уникальными свойствами и вызывает приятное чувство эстетики.
Когда мы говорим о вложении окружности в прямоугольный треугольник с прямым углом, мы обращаем внимание на особенность расположения окружности относительно сторон треугольника. Здесь важными являются разнообразные синонимы, такие как "содержание", "содержимое", "расположение" и т.д.
Эта задача требует внимательного анализа сторон и углов треугольника, чтобы определить точное положение окружности. Важно помнить, что окружность должна быть полностью вписана в треугольник, прикосаясь к каждой из его сторон. Перестраивая структуру предложения, мы можем использовать синонимы "точное местоположение", "точка касания" и "все стороны треугольника", чтобы избежать повторений и добавить разнообразия.
Наличие прямого угла в треугольнике играет важную роль в подборе размеров окружности. Благодаря этому свойству, окружность повторяет геометрическую структуру треугольника, что создает гармоничное сочетание и придает общему изображению баланс и красоту. Замена слов "подразумевать", "свойство" и "изображение" позволяет статье звучать более разнообразно.
Однако, важно помнить, что вложение окружности в треугольник с прямым углом требует точного расчета и рассмотрения геометрических свойств. Это задача, которая привлекает внимание математиков и эстетов, поскольку сочетает в себе точность и гармонию геометрии.
Раздел: Применение теоремы Пифагора для рисования вписанной окружности

Для начала, представим себе произвольный треугольник, у которого один из углов является прямым. Мы будем исследовать способы определить радиус вписанной окружности, когда известны стороны треугольника.
Используя теорему Пифагора, мы можем получить соотношение между сторонами прямоугольного треугольника. Зная эти соотношения, можно вывести формулу для радиуса вписанной окружности, связывающую его с длиной сторон треугольника. Данная формула позволит эффективно находить радиус и, следовательно, построить окружность, вписанную в треугольник.
Мы представим эти соотношения в таблице ниже, чтобы было удобнее проводить вычисления и наглядно представить полученные результаты:
| Сторона треугольника | Формула соотношения с радиусом |
|---|---|
| Сторона A | Радиус = (A*B*C) / (2 * Периметр) |
| Сторона B | Радиус = (A*B*C) / (2 * Периметр) |
| Гипотенуза C | Радиус = (A*B*C) / (2 * Периметр) |
С помощью полученной формулы и данных о сторонах треугольника, можно вычислить радиус вписанной окружности и, таким образом, точно вписать окружность в треугольник.
Взаимосвязь изменения размеров треугольника и его вписанной окружности
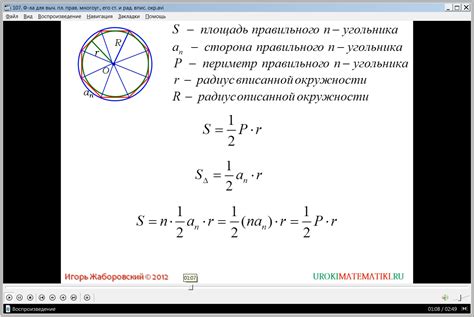
Величина сторон прямоугольного треугольника оказывает непосредственное влияние на размер и положение вписанной окружности. При изменении длин сторон треугольника происходят соответствующие изменения в размере и положении окружности, которая вписана в этот треугольник. Это феноменальное взаимодействие между геометрическими элементами наглядно демонстрирует, как изменение размера прямоугольного треугольника влияет на центр и радиус его вписанной окружности, а также на сегменты треугольника, которые касаются окружности.
Увеличение или уменьшение размеров сторон треугольника приводит к соответствующему изменению величины радиуса вписанной окружности. Если сторона треугольника увеличивается, то радиус окружности становится больше, в то время как уменьшение стороны треугольника приводит к сокращению радиуса окружности.
Кроме того, изменение размеров треугольника также влияет на положение центра вписанной окружности. При увеличении размеров сторон треугольника центр окружности смещается в сторону прямого угла, а при уменьшении размеров сторон треугольника центр окружности смещается в сторону острых углов треугольника.
Практическое применение эффекта вписанной окружности в прямоугольном треугольнике
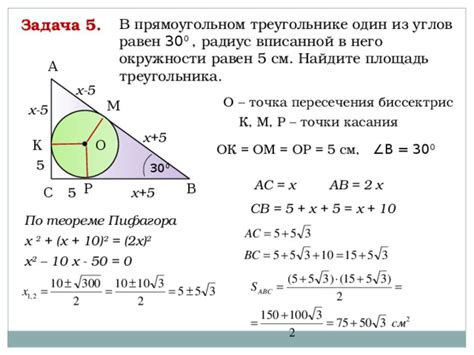
- Математика: Вписанная окружность позволяет упростить вычисления в прямоугольном треугольнике и использовать его особенности для получения точных результатов. К примеру, можно использовать окружность для определения центра масс треугольника или для вычисления длины сторон и углов треугольника.
- Архитектура и строительство: При планировке зданий и сооружений применение вписанной окружности может помочь оптимизировать расположение стен и элементов конструкции, увеличить энергетическую эффективность и создать гармоничный дизайн.
- Графика и дизайн: Вписанная окружность представляет собой эстетически приятную форму, которую можно использовать при создании иллюстраций, логотипов, шаблонов и других графических элементов. Она помогает создать сбалансированный и гармоничный дизайн.
Эффект вписанной окружности в прямоугольном треугольнике является универсальным инструментом, который может быть применен в различных областях. Умение использовать этот эффект позволяет решать задачи с использованием геометрических принципов, обеспечивая точность и эстетическую привлекательность решений.
Вопрос-ответ

Как вписать окружность в прямоугольный треугольник?
Для вписывания окружности в прямоугольный треугольник нужно провести серединные перпендикуляры к каждой из его сторон. Пересечение этих перпендикуляров будет центром вписанной окружности, а радиусом окружности будет расстояние от центра до любой из сторон треугольника. При правильном выполнении этих шагов окружность полностью поместится внутрь треугольника.
Как найти радиус вписанной окружности в прямоугольном треугольнике?
Чтобы найти радиус вписанной окружности в прямоугольном треугольнике, нужно найти полупериметр треугольника, который вычисляется по формуле p = (a + b + c) / 2, где a, b и c - длины сторон треугольника. Затем, используя формулу радиуса вписанной окружности r = S / p, где S - площадь треугольника, а p - полупериметр, можно найти радиус окружности. Обратите внимание, что площадь треугольника можно найти, используя формулу Герона.
Как провести серединные перпендикуляры к сторонам прямоугольного треугольника?
Для того чтобы провести серединные перпендикуляры к сторонам прямоугольного треугольника, нужно найти середины каждой из сторон, используя формулу (x1 + x2) / 2 и (y1 + y2) / 2 для координат точек. Затем, для каждой стороны проводим прямую, проходящую через найденные середины и перпендикулярную этой стороне. Точка пересечения всех этих перпендикуляров будет являться центром вписанной окружности.
Возможно ли вписать окружность в прямоугольный треугольник, у которого все стороны разной длины?
Да, возможно вписать окружность в прямоугольный треугольник, у которого все стороны разной длины. Условие прямого угла между сторонами треугольника является основным требованием для вписывания окружности. Длины сторон не играют особой роли, главное чтобы треугольник был прямоугольным.
Как вписать окружность в прямоугольный треугольник?
Для вписывания окружности в прямоугольный треугольник необходимо провести биссектрисы углов треугольника и их пересечение будет центром окружности, описанной вокруг треугольника. Чтобы найти радиус окружности, нужно взять половину длины наименьшей стороны треугольника.
Какие инструменты понадобятся для вписывания окружности в прямоугольный треугольник?
Для вписывания окружности в прямоугольный треугольник потребуются линейка и циркуль. Линейкой необходимо провести биссектрисы углов треугольника, а циркулем можно измерить радиус окружности, который будет равен половине длины наименьшей стороны треугольника.



