Представьте себе, что вы потеряли все важное знание, полученное в течение многих лет обучения. Как бы вы смогли восстановить основы школьной математики? В этой статье мы предлагаем вам краткий курс, в котором вы сможете вспомнить все важные темы и понять их значение в современном мире.
Алгебра: это не просто набор букв и чисел на бумаге. Она является языком, с помощью которого мы можем описывать и анализировать различные математические отношения и структуры. Вспомните, как решать уравнения и неравенства, как упрощать выражения и находить значения переменных.
Геометрия: это наука о формах и пространстве. Она помогает нам понять, как строить и анализировать фигуры, а также решать различные геометрические задачи. Вспомните, как измерять углы, находить площади и объемы, а также как использовать теоремы и свойства для доказательства геометрических утверждений.
Статистика: ее значение в современном мире трудно переоценить. Она помогает нам собирать, анализировать и интерпретировать данные, чтобы принимать обоснованные решения. Вспомните, как находить средние значения, строить графики и диаграммы, а также использовать вероятность для прогнозирования событий.
История математики: открытия и достижения
Изучение истории математики позволяет нам не только ознакомиться с прошлыми достижениями, но и понять, какие принципы и методы использовались для решения математических задач, исторические контексты использования этих знаний и их влияние на общество.
Разбираясь с историей математики, мы можем узнать о знаменитых математиках прошлого, таких как Пифагор, Евклид, Архимед, Фибоначчи и многих других, их творческих и научных открытиях, которые стали основой для развития современной математики.
Будучи одной из старейших наук, математика в своей истории прошла непростой путь эволюции. Она развивалась на протяжении многих столетий, вносила вклад в разные области научного знания, неизменно привлекая к себе внимание ученых и математиков разных поколений. Открытия и достижения этих ученых существенно изменили нашу жизнь и вселенную, раскрывая перед нами новые горизонты и позволяя более полно понять некоторые законы и принципы, лежащие в основе этой науки.
- История математики демонстрирует несокрушимый ум человечества и его постоянное стремление к познанию истины.
- Каждое историческое открытие в математике отражает значимость и роль этой науки в развитии культуры и цивилизации.
- Изучение истории математики позволяет увидеть непрерывность и наследие идеи, которые связывают нас с пониманием и использованием математических знаний.
История математики дает нам возможность заглянуть в прошлое, оценить идеи и труды великих умов, а также восхититься их достижениями. Изучение истории математики помогает понять ее ценность и роль в современном мире и вдохновляет на новые открытия и развитие.
Путь математики: эволюция с древности до наших дней

Исследование развития математики от истоков до современности открывает перед нами удивительный путь, пропитанный творчеством и открытиями великих умов. Как лазурная нить, математика пронизывает эпохи и цивилизации, служа непременным инструментом для понимания мира и решения сложных задач.
Древние цивилизации
Глубокий корень математики уходит в архаическую эпоху. Бабилонцы и египтяне разработали системы счисления, использование которых позволяло им решать практические задачи. Древнегреческие философы, в частности Пифагор, Эвклид и Архимед, не только расширили базу математических знаний, но и внесли вклад в создание геометрии и алгебры.
Средневековье и Возрождение
Средние века, хотя и славятся преобладанием религиозной доктрины, были не лишены вклада в развитие математики. Арабские ученые сохранили и распространили древние знания, усовершенствовав алгебру и внедрив в Европу индо-арабскую систему счисления. Затем наступила эпоха Возрождения, великие математики которого, такие как Леонардо Пизанский (Фибоначчи), Николай Коперник и Иоганн Кеплер, сделали ставку на опытные исследования и создали фундамент для будущих открытий.
Наука и технологический век
В девятнадцатом и двадцатом веках математика приобрела новое значение в силу развития науки и технологии. Открывая двери к промышленному революционному прогрессу, ученые, включая Карла Гаусса, Леонарда Эйлера и Аду Лавлейс, разработали новые теории и методы, направившие математику в исследование сложных функций, статистики и компьютерных наук.
Современность
В наше время математика стала мощным инструментом для моделирования сложных систем, разработки криптографии, исследования машинного обучения и экономических процессов. С появлением новых концепций, таких как теория хаоса и фракталов, математика продолжает расширять свои границы и искать новые пути понимания мира.
Развитие математики с древних времен до наших дней свидетельствует о постоянной эволюции нашего понимания, построенного на труде и стойкости великих умов, которые позволяют нам узнать и создать больше в этом невероятном мире чисел и формул.
Основы алгебры: ключевые концепции и операции

Этот раздел посвящен основным понятиям и операциям в алгебре, одной из фундаментальных областей математики. Здесь мы рассмотрим ключевые принципы и инструменты, которые позволяют решать сложные математические задачи, а также понимать взаимосвязи между различными математическими явлениями.
Основные понятия алгебры включают в себя такие термины, как переменная, уравнение, функция, неравенство и многое другое. Мы рассмотрим, как эти понятия связаны между собой и как они используются для анализа и решения различных задач.
| Операция | Описание |
|---|---|
| Сложение | Операция, которая объединяет два или более числа в одно число. |
| Вычитание | Операция, противоположная сложению; позволяет находить разность между двумя числами. |
| Умножение | Операция, которая позволяет находить произведение двух или более чисел. |
| Деление | Операция, противоположная умножению; позволяет находить частное между двумя числами. |
Важно понимать, что эти операции можно применять не только к числам, но и к другим объектам, таким как переменные и функции. Алгебра также изучает различные свойства и законы этих операций, которые являются основой для дальнейшего изучения более сложных тем, таких как системы уравнений, матрицы и теория групп.
Изучение алгебры: от простых уравнений до систем линейных уравнений

Помимо освоения решения уравнений, вы также изучите системы линейных уравнений. Системы линейных уравнений являются наборами уравнений, которые связаны друг с другом и имеют общие переменные. Важной частью изучения алгебры, является развитие навыков работы с системами линейных уравнений. Вы научитесь классифицировать системы уравнений, определять их решения и применять методы решения, такие как метод подстановки и метод сложения и вычитания.
Изучение алгебры предоставляет вам не только инструменты для решения уравнений и систем, но также помогает развить аналитическое мышление, логику и абстрактное мышление. Вы сможете применять эти навыки в решении повседневных задач и более сложных математических проблем. Знание алгебры также является важным фундаментом для изучения более продвинутых математических тем, таких как геометрия, тригонометрия и анализ.
Таким образом, раздел "Изучение алгебры: от простых уравнений до систем линейных уравнений" представляет собой комплексное введение в алгебру, содержащее основные понятия, методы решения уравнений и систем. Он позволяет вам развить навыки работы с уравнениями разных видов и приобрести необходимые навыки для успешного продвижения в области математики и применения ее в повседневной жизни.
Геометрия: формы и пространство
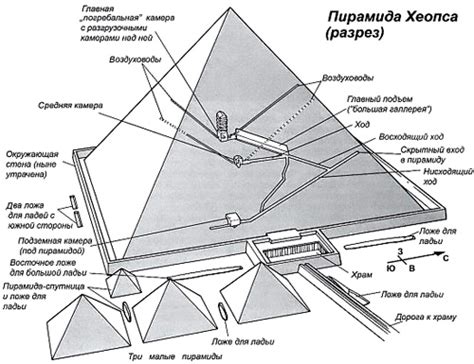
Изучение геометрии открывает перед нами захватывающий мир форм и пространства, позволяя нам углубить понимание окружающего нас мира. В данном разделе мы погрузимся в многообразие геометрических фигур и исследуем свойства пространства.
Фигуры – это основные элементы геометрии, которые встречаются в повседневной жизни и имеют свои уникальные свойства. Мы углубимся в изучение таких форм, как треугольники, квадраты, прямоугольники, круги и многое другое. Важно отметить, что каждая фигура имеет свои характеристики, такие как количество сторон, углы, длины и периметры.
Пространство – это понятие, которое помогает нам описать расположение объектов в трехмерном мире. Мы изучим объемы и поверхности пространственных фигур, таких как кубы, цилиндры и конусы. Также мы узнаем о различных системах координат и способах измерения расстояний в пространстве.
Изучение геометрии развивает наше пространственное воображение, аналитическое мышление и умение абстрагироваться от конкретных объектов. Независимо от того, являетесь ли вы будущим инженером, архитектором или просто интересуетесь миром геометрии, этот раздел поможет вам обрести новые знания и расширить свой кругозор в области геометрии и пространства.
Изучение геометрии: от плоских фигур до трехмерных объектов
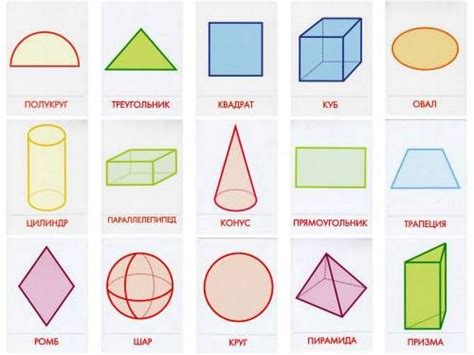
В этом разделе мы рассмотрим важные аспекты геометрии, которые помогут углубить наши знания и понимание пространственных форм.
Будем изучать различные типы плоских фигур, такие как треугольники, квадраты, прямоугольники и круги. Узнаем их основные характеристики, такие как количество сторон, углов и свойства.
Далее мы перейдем к трехмерным объектам, таким как кубы, цилиндры, конусы и сферы. Узнаем, как эти объекты выглядят в трехмерном пространстве и как связаны их размеры, объемы и площади поверхности.
Важным аспектом изучения геометрии является также понимание пространственных отношений, таких как расстояния и углы между объектами. Узнаем, как проводить измерения и решать задачи, используя принципы геометрии.
Изучение геометрии поможет нам развить навыки логического мышления, абстрактного мышления и пространственной интуиции, которые являются важными в различных областях жизни и науки.
Тригонометрия: основы работы с углами и тригонометрическими функциями

Изучение тригонометрии поможет вам лучше понять связь между углами и сторонами в геометрических фигурах, а также в анализе и моделировании различных явлений. Тригонометрические функции играют ключевую роль в решении задач, связанных с определением углов, нахождением длин сторон треугольников и измерением различных циклических явлений.
В этом разделе мы рассмотрим базовые понятия тригонометрии, такие как синус, косинус и тангенс. Мы изучим их определения и свойства, а также научимся применять эти функции для решения различных задач. Углы являются основными понятиями в тригонометрии, поэтому мы также рассмотрим способы измерения и представления углов, а также научимся работать с градусами и радианами.
Важно понимать, что тригонометрия имеет широкий применительный потенциал, и наши знания в этой области будут полезны во многих других областях, таких как физика, инженерия, астрономия и экономика. Поэтому интуитивное понимание тригонометрии и умение применять ее методы и формулы могут стать незаменимыми навыками в вашей будущей профессиональной деятельности.
Давайте начнем изучение основ тригонометрии и угловых функций, чтобы расширить наши знания в математике и подготовиться к решению сложных задач и проблем в реальном мире. И помните, что практика и постоянное обращение с углами и тригонометрическими функциями помогут вам стать опытным математиком!
Вопрос-ответ

Какие темы рассматривает статья "Вспомните все важные темы школьной математики: краткий курс"?
Статья обзорно рассматривает все основные темы школьной математики, включая арифметику, геометрию, алгебру, статистику и вероятность.
Каким образом статья описывает арифметику?
Статья описывает основные операции арифметики, такие как сложение, вычитание, умножение и деление чисел, а также дает примеры и объяснения применения этих операций в реальной жизни.
Какие темы геометрии рассматривает статья?
Статья рассматривает различные геометрические фигуры, такие как треугольники, прямоугольники, круги, а также объясняет основные понятия, такие как периметр, площадь и объем. Более подробно описывается геометрия на плоскости и в пространстве.
Какие основные концепции алгебры рассматривает статья?
Статья рассматривает основные понятия алгебры, такие как переменные, уравнения, неравенства, функции и графики. Также описывается применение алгебры в решении задач и примеры практического использования.
Какие аспекты статистики и вероятности освещаются в статье?
Статья освещает основные понятия статистики, такие как среднее значение, медиана, мода, дисперсия. Также рассматривается основы вероятности и объясняется, как решать задачи с использованием вероятностных методов.
Какие темы входят в школьный курс математики?
В школьный курс математики входят различные темы, например, арифметика (сложение, вычитание, умножение, деление), геометрия (фигуры, углы, площади, объемы), алгебра (уравнения, системы уравнений, графики функций), математическая логика, статистика и вероятность.



