Во вселенной геометрических объектов есть нечто, что привлекает взгляд и заставляет задуматься о своей природе. Возможно, это именно вектор, тот загадочный графический образ, который олицетворяет направление и длину. Два независимых понятия, которые объединяются и вместе создают волнующую картину, с которой мы имеем возможность работать. Однако, чтобы понять значение вектора, необходимо погрузиться в мир координатных систем и раскрыть смысл его компонентов.
Мы живем в трехмерном пространстве, где каждая точка можно описать с помощью нескольких параметров. Вектор в свою очередь, является чудесным инструментом для описания объектов и всех процессов, происходящих в пространстве. Важно осознать, что сам вектор не имеет ни начала, ни конца, он просто это прямая линия, которая может быть перенесена на любом удобном нам участке пространства. Чтобы определить положение вектора, необходимо использовать координаты.
Запомните, координаты - это числа, которые определяют позицию объекта в пространстве. Они являются основными элементами двумерных и трехмерных систем координат. Заключаются в себе два значения, аналогичные двумерной координатной плоскости, которые позволяют определить местоположение объекта. Каждая величина из этой пары чисел может называться компонентой вектора. При этом, две компоненты вектора могут принимать положительное или отрицательное значение, и их комбинации дают возможность установить положение вектора в пространстве.
Зачем нужна система координат и что она представляет?

В мире, где мы живем, множество объектов и явлений можно описывать и изучать с помощью различных числовых параметров. Однако, для удобства и единообразия, необходимо иметь установленную систему, с помощью которой можно было бы определить позицию и направление этих числовых параметров. Система координат представляет собой набор правил, ориентированных на определение точки или объекта в пространстве в соответствии с выбранными единицами измерения.
Система координат позволяет нам легче работать с объектами, описывать их положение, перемещение и пространственные отношения. Она также дает возможность визуализировать данные и конкретизировать информацию, делая ее более понятной и удобной для обработки. Это позволяет нам анализировать и изучать объекты и явления с помощью математических методов и моделей.
В системе координат можно определять положение объектов с помощью числовых значений, называемых координатами. Одни объекты могут иметь одну координату, такую как расстояние от начала системы координат до объекта, в то время как другие объекты могут иметь две, три и даже более координат. Зная эти координаты, мы можем точно указать местоположение объекта в пространстве и сравнивать его с другими объектами или проводить измерения и расчеты.
Система координат имеет различные типы, такие как прямоугольная система координат, полярная система координат, сферическая система координат и многие другие. Каждая система координат имеет свои особенности и применение в разных областях науки и инженерии, что делает ее важным инструментом для работы с числовыми данными и понимания пространственных отношений.
Преобразование положения точки в прямоугольной системе координат
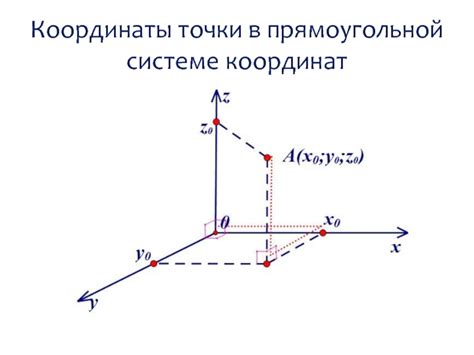
Преобразование координат векторов позволяет изменять их положение и направление в прямоугольной системе координат. Такие преобразования могут быть полезными для перемещения объектов, а также для решения геометрических задач и вычислений.
- Сдвиг: одним из наиболее распространенных преобразований координат является сдвиг. Он позволяет изменить положение вектора на определенное расстояние в заданном направлении.
- Масштабирование: данное преобразование изменяет длину вектора без изменения его направления. Оно может быть полезно, например, для изменения размера объекта на экране.
- Поворот: поворот позволяет изменить направление вектора, сохраняя его длину. Это полезное преобразование при работе с ориентацией объекта или при решении задач с вращением.
- Отражение: отражение меняет направление вектора относительно заданной оси. Это полезное преобразование во многих контекстах, включая зеркальное отображение или симметрию относительно определенной линии.
Преобразование координат векторов в прямоугольной системе координат представляет собой мощный инструмент для анализа и манипулирования геометрическими объектами. Понимание и использование этих преобразований позволяет увидеть и решить различные геометрические задачи в более эффективный и гибкий способ.
Основные характеристики вектора и его разложение на компоненты в прямоугольной системе координат
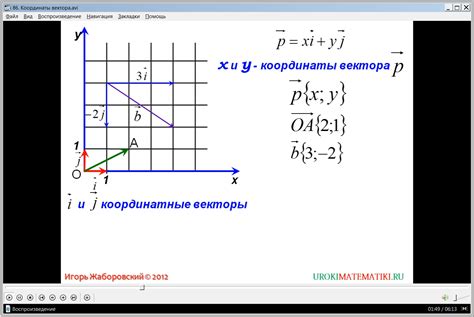
Вектор характеризуется не только величиной, но и направлением. Это позволяет описывать перемещения объекта относительно начальной точки координатной системы. Координаты вектора представляют собой числа, указывающие на его перемещение вдоль каждой из осей координат.
Разложение вектора на компоненты в прямоугольной системе координат позволяет удобно описывать его перемещение и оперировать с ним в математических выражениях. Компоненты вектора обозначаются символами, которые отражают его перемещение по соответствующей оси координат.
Проекция вектора на оси координат представляет собой компоненты вектора, которые указывают его перемещение по каждой из осей. Обычно проекции вектора представляются числами с указанием знака, отражающим его направление в положительном или отрицательном направлении от начала координатной оси.
Если вектор перемещается по оси X, его координата по оси Y будет равна 0, и наоборот.
Для описания положительного направления осей координат могут применяться термины "плюс" и "минус", "вперед" и "назад", "влево" и "вправо".
Таким образом, разложение вектора на компоненты в прямоугольной системе координат упрощает его описание и позволяет проводить различные математические операции с векторами, ориентируясь на их координаты.
Базисные векторы: основа прямоугольной системы координат
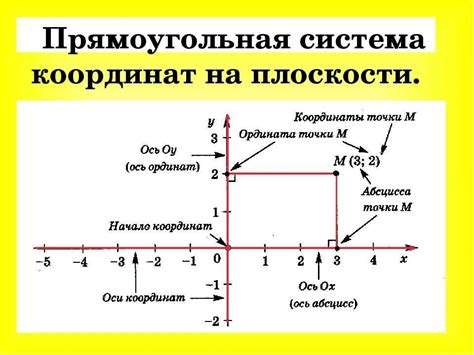
Каждая ось координат имеет свой соответствующий базисный вектор. Ось X соответствует горизонтальному направлению, а ось Y – вертикальному. Все остальные направления в системе координат определяются относительно этих двух базисных векторов.
Базисные векторы играют ключевую роль в определении положения и перемещения объектов в прямоугольной системе координат. Координаты вектора в такой системе задаются в терминах его компонентов, которые выражаются через базисные векторы. Оси координат служат важным инструментом для проведения измерений, а также для описания и анализа различных явлений и процессов.
- Базисные векторы являются ортогональными направлениями и образуют оси координат.
- Ось X соответствует горизонтальному направлению, а ось Y – вертикальному.
- Базисные векторы позволяют однозначно определить положение любой точки в прямоугольной системе координат.
- Компоненты вектора выражаются через базисные векторы и задают его координаты.
- Базисные векторы играют ключевую роль в определении положения и перемещения объектов в системе координат.
Различные подходы к определению координат вектора в прямоугольной системе координат
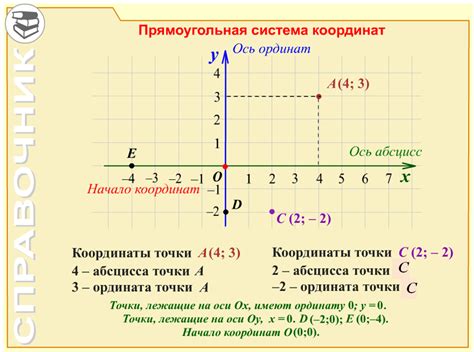
В рамках прямоугольной системы координат, существует несколько способов определить координаты вектора, при этом каждый из них подчеркивает различные аспекты и особенности данной математической концепции.
Один из подходов основан на использовании числовых значений для задания положения вектора на плоскости. В этом случае, вектор представляется парой чисел, которые указывают на расстояние от начала координат до конечной точки вектора вдоль осей X и Y соответственно. Таким образом, первое число описывает горизонтальное положение вектора, а второе числовое значение - вертикальное положение.
Второй подход ориентирован на использование угловой меры для определения координат вектора. Здесь вектор представляется начальной точкой, углом относительно положительного направления оси X и длиной вектора. Таким образом, вектор задается углом наклона и длиной от начала координат до конечной точки.
Кроме того, стоит отметить, что существует возможность использования комплексных чисел для определения координат вектора в прямоугольной системе координат. В этом случае, координаты вектора задаются парой комплексных чисел, где действительная часть представляет горизонтальную составляющую, а мнимая часть - вертикальную. Таким образом, комплексные числа позволяют использовать алгебраические операции для работы с координатами вектора на плоскости.
В зависимости от ситуации и поставленной задачи, один из этих методов может быть предпочтительнее другого. Поэтому, важно понимать и уметь применять различные способы определения координат вектора в прямоугольной системе координат с учетом их особенностей и потенциальных преимуществ.
Вычисление значений компонент вектора при известных показателях его составляющих
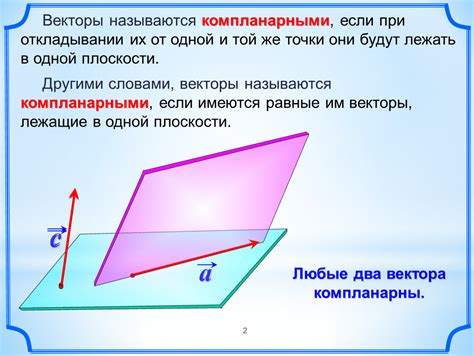
Рассмотрим методику для определения значений компонент вектора в прямоугольной системе координат, основанную на известных данных. Путем использования известных значений компонент и соответствующих формул можно вычислить координаты и направление вектора.
Для того чтобы вычислить значения компонент вектора, необходимо знать его направление и его длину. Направление вектора определяется углом, который образует вектор с положительным направлением оси X, а его длина (магнитуда) может быть задана числовым значением.
Для определения значений компонент вектора воспользуемся тригонометрическими функциями и знаниями об угле, который вектор образует с положительным направлением оси X. Например, если известна длина вектора и его угол с положительным направлением оси X, то можно определить значения его горизонтальной (X) и вертикальной (Y) компонент. Для этого применяются следующие формулы:
X = длина вектора * cos(угол)
Y = длина вектора * sin(угол)
Таким образом, при наличии известного значения длины вектора и угла, его компоненты могут быть определены посредством применения тригонометрических функций. Этот подход обеспечивает возможность вычисления координат вектора на плоскости в прямоугольной системе координат.
Графическое изображение расположения точек на плоскости
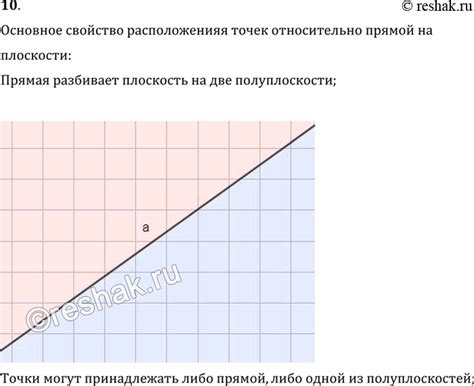
В предыдущих разделах мы рассмотрели понятия координат, вектора и прямоугольной системы координат. Теперь перейдем к рассмотрению графического представления координат вектора в такой системе.
Графическое представление координат вектора в прямоугольной системе координат позволяет наглядно отобразить его расположение на плоскости. Изображение точки на плоскости определяется ее координатами. В данном случае, каждой точке ставятся в соответствие две числовые величины - x-координата и y-координата, определенные в декартовой системе координат.
Для графического представления используется система координат, которая состоит из двух перпендикулярных осей - горизонтальной x-оси и вертикальной y-оси. Начало координат, точка с координатами (0, 0), находится в их пересечении.
Для графического изображения вектора на плоскости необходимо указать ее начало и направление. Начало вектора соответствует началу координат, а направление определяется его координатами или углом относительно положительного направления осей.
Чтобы изобразить вектор с заданными координатами, проводят от начала координат линию, параллельную одной из осей, длиной, пропорциональной заданным значениям координат. Конец этой линии является конечной точкой вектора. Таким образом, графическое представление вектора - это отрезок, заданный его координатами.
Вопрос-ответ

Какие существуют преимущества использования прямоугольной системы координат?
Преимущества использования прямоугольной системы координат включают: простоту применения, удобство для математического анализа и решения геометрических задач, возможность однозначной интерпретации каждой точки на плоскости с помощью двух чисел.
Как определяются координаты вектора в прямоугольной системе координат?
Координаты вектора в прямоугольной системе координат определяются с помощью осей координат. Первая координата - это проекция вектора на горизонтальную ось (обычно ось x), а вторая координата - это проекция вектора на вертикальную ось (обычно ось y).
Какая связь существует между координатами вектора и его направлением?
Связь между координатами вектора и его направлением заключается в том, что изменение координат вектора приводит к изменению его направления. Если мы изменяем одну из координат, то вектор смещается вдоль соответствующей оси, что изменяет его направление. Например, если увеличиваем координату x, то вектор смещается вправо, а если увеличиваем координату y, то вектор смещается вверх.
Как можно найти модуль вектора по его координатам в прямоугольной системе координат?
Модуль вектора может быть найден с использованием теоремы Пифагора. Для вектора с координатами (x, y) его модуль вычисляется как квадратный корень из x^2 + y^2.



