Если вы когда-либо сталкивались с необходимостью визуализировать функции в виде графиков, то вы, вероятно, знаете, как важен этот навык. Графики функций помогают отслеживать и анализировать изменения величин, а также исследовать их взаимосвязи.
Вместе с тем, создание графиков функций может быть вызовом для многих. Некоторые может пугает идея рисования на графическом листе или использование сложных программ для визуализации. Однако не волнуйтесь! Мы предлагаем вам простое руководство, которое поможет вам нарисовать базовый эскиз графика функции без утомительных трудозатрат и сложных инструментов.
В этой статье мы подробно разберем все этапы создания графика функции. Мы покажем вам, как начать с построения осей координат и разбить их на равные интервалы. Затем мы рассмотрим, как выбрать значения для каждой оси и как обозначить их на графике. Кроме того, вы узнаете о методах построения графиков различных функциональных зависимостей.
Выбор подходящей функции для создания эскиза графика
Перед началом работы нам необходимо определить, какое именно сообщение или идею мы хотим передать через график. Для этого нужно четко сформулировать цель создания эскиза. Например, мы можем хотеть показать рост или снижение какой-то величины со временем, иллюстрировать изменение одной переменной при изменении другой или сравнивать несколько функций и их поведение.
Далее, важно оценить характеристики выбранного графика. Нам нужно понять, какая функция может лучше всего отразить требуемое поведение. Например, если мы хотим показать экспоненциальный рост, то логарифмическая функция может оказаться подходящей. Если мы ищем аппроксимацию кривой, то полиномиальная функция может дать более точное представление. Если нам нужно показать изменение переменной во времени, то временные ряды или синусоидальные функции могут быть полезными.
Кроме того, при выборе функции мы должны учитывать ее математические свойства. Например, если график должен быть гладким, то нам потребуется функция с непрерывной производной. Если мы хотим показать периодическое поведение, то синусоидальные функции будут более уместными.
И наконец, не стоит забывать о визуальной привлекательности графика. Построение графика с помощью художественного подхода может придать ему дополнительную эстетическую ценность и помочь привлечь внимание зрителя.
Определение области, в которой функция определена
В данном разделе мы рассмотрим понятие области определения функции, то есть множество всех значений аргумента функции, при которых она определена и имеет смысл. Знание области определения позволяет правильно построить график функции и избежать ошибок при проведении геометрических конструкций.
Каждая функция имеет свои особенности и ограничения, определяющие ее область определения. Рассмотрим несколько примеров для наглядной иллюстрации. Например, в функции, описывающей зависимость площади круга от радиуса, область определения будет представлять собой множество положительных чисел, так как отрицательный радиус не имеет физического смысла. В другом случае, функция, описывающая зависимость стоимости проезда на такси от пройденного расстояния, будет иметь область определения, состоящую из всех неотрицательных чисел, так как невозможно проехать отрицательное расстояние.
Важно отметить, что область определения может быть ограничена не только числами, но и другими условиями, такими как доступные ресурсы, физические ограничения или принятые конвенции. Поэтому при изучении и построении графиков функций необходимо учитывать все эти факторы.
Итак, определение области определения функции является ключевым шагом в построении ее графика. Это позволяет исключить недопустимые значения аргумента и гарантировать правильность построения графического представления функции. Учитывая различные особенности функций, следует всегда проверять и анализировать ее область определения перед началом работы с функциональными графиками.
Определение точек пересечения с осями координат
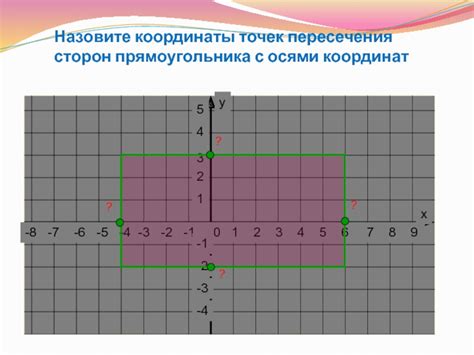
В этом разделе мы рассмотрим методы определения точек пересечения графика функции с осями координат. Найдя эти точки, мы сможем получить дополнительную информацию о поведении функции и ее свойствах.
Пересечение графика функции с осью абсцисс (ось X) происходит в точках, где значение функции равно нулю. Для нахождения этих точек, необходимо решить уравнение f(x) = 0, где f(x) - функция, график которой мы рассматриваем. Это можно сделать аналитически, используя методы решения уравнений либо приближенно, находя корни с помощью численных методов.
Пересечение графика функции с осью ординат (ось Y) происходит в точке, где значение аргумента равно нулю. Аргумент, соответствующий этой точке, можно найти, подставив y = 0 в уравнение функции f(x). После этого необходимо решить полученное уравнение относительно x. В результате получим координаты точки, в которой график функции пересекает ось Y.
Найденные точки пересечения с осями координат могут дать нам полезную информацию о функции, такую как четность/нечетность функции, наличие симметрии, экстремумы и другие характеристики функции. Это позволяет нам более глубоко изучить поведение функции и составить более полное представление о ее свойствах.
Анализ поведения функции в пределах области определения

В данном разделе мы подробно рассмотрим поведение функции в пределах ее области определения. Мы изучим, как функция изменяется при различных значениях аргумента и какие особенности могут возникать на графике функции.
Анализ поведения функции включает в себя такие аспекты, как определение области определения, поиск вертикальных и горизонтальных асимптот, нахождение точек разрыва и экстремумов функции.
Для начала определим область определения функции - множество значений аргумента, при которых функция имеет смысл. Мы изучим, какие значения аргумента могут использоваться для нашей функции и какие значения следует исключить.
Далее мы будем исследовать асимптоты функции. Вертикальные асимптоты - это вертикальные линии, к которым график функции стремится при достаточно больших и малых значениях аргумента. Горизонтальные асимптоты - это горизонтальные линии, к которым график функции стремится при изменении аргумента в бесконечности.
Также мы исследуем точки разрыва функции, которые могут возникать при делении на ноль или извлечении корня из отрицательного числа. Они могут приводить к нарушению непрерывности графика функции и иметь особые значения в контексте функции.
Наконец, мы изучим экстремумы функции - точки, где функция достигает максимального или минимального значения. Мы будем искать максимальные и минимальные значения функции в ее области определения с помощью производных и критериев экстремума.
Нахождение ключевых точек графика: экстремумы, точки разрыва и изломов
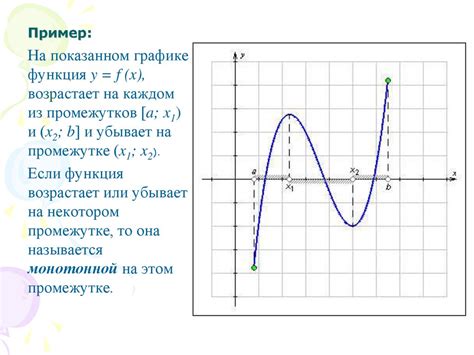
Этот раздел посвящен поиску и определению особых точек на графике функции. Изучение таких точек позволяет нам лучше понять поведение функции и ее свойства. Они могут быть представлены различными способами, включая экстремумы, точки разрыва и изломы.
Экстремумы представляют собой точки на графике, в которых функция достигает локального максимума или минимума. Важно заметить, что экстремумы могут быть как абсолютными (глобальными), так и относительными (локальными). Они могут иметь различные формы - максимумы, минимумы или быть подобными точке перегиба.
- Перегибы представляют собой точки, в которых график изменяет свое направление, то есть кривизна графика меняется. Изломы могут быть положительными, когда график становится выпуклым вверх, или отрицательными, когда график становится выпуклым вниз.
- Точки разрыва - это точки, в которых график функции разрывается или не имеет определения. Они могут быть вертикальными разрывами, когда функция не определена при определенном значении аргумента, или горизонтальными разрывами, когда функция имеет разные значения при приближении аргумента с разных сторон.
Понимание и определение экстремумов, точек разрыва и изломов является важным шагом в построении графика функции. Это дает нам возможность увидеть особенности функции и ее поведение на различных участках графика. Дальнейший анализ и использование этих точек может помочь нам в решении различных математических и практических задач.
Бессамовращающиеся линии и визуальное представление функций
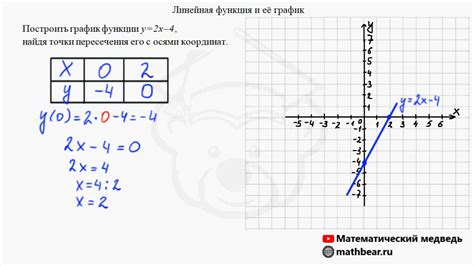
Вы можете выбрать разные способы соединения точек, в зависимости от того, что вы хотите передать своим зрителям. Например, вы можете использовать сплошные линии, чтобы подчеркнуть непрерывность функции. Этот метод пригоден, когда функция гладкая и не имеет разрывов или скачков. Если же функция имеет особые точки или разрывы, то может быть полезным использование прерывистых или пунктирных линий для подчеркивания этих особенностей.
Рисование графика функции - это творческий процесс, в котором вы можете использовать свою интуицию и вкус. Помимо стиля линий, можно экспериментировать с толщиной и цветом. Вы можете использовать разные цвета для разных частей графика или подобрать единый цветовой акцент. Также не забывайте о том, что график функции должен быть читаемым и понятным, поэтому выбирайте стиль и цвет, которые максимально выделяют вашу функцию и делают ее различимой от других линий на графике.
Итак, соединение полученных точек и рисование графика функции - это искусство передачи информации о функции через визуальное представление. Подумайте о том, какой стиль, толщина и цвет наилучшим образом передадут особенности и идею вашей функции. Экспериментируйте с разными вариантами и найдите оптимальное решение, чтобы ваш график был не только корректным математическим представлением функции, но и интересным и привлекательным визуально.
Проверка достоверности и точности полученного наброска картинки графика функции

В этом разделе мы рассмотрим важность проверки корректности и точности эскиза графика функции. После того, как вы завершите создание эскиза и представление графика функции, необходимо убедиться в том, что полученное изображение корректно и отражает функцию достоверно и точно.
В ходе проверки следует уделить внимание следующим аспектам:
- Анализ внешнего вида графика. Оцените, насколько линии графика плавные и позволяют легко определить тенденцию функции. Убедитесь, что график отображает основные характеристики функции, такие как возрастание, убывание, экстремумы и асимптоты.
- Соответствие графика математическим свойствам функции. Проверьте, что график отражает все математические свойства функции, такие как границы области определения, асимптоты, точки перегиба и особые точки.
- Сравнение с известными значениями функции. Сравните полученный график с известными значениями функции в выбранных точках. Проверьте, что график соответствует ожидаемым значениям и не содержит значительных отклонений.
- Проверка на ошибки. Внимательно просмотрите эскиз графика на наличие ошибок, таких как неправильное построение линий или забытые элементы графика. Убедитесь, что все линии и элементы графика соответствуют заданным условиям и ожиданиям.
Проверка полученного эскиза на корректность и точность является важным этапом в создании графика функции. Она позволяет убедиться в достоверности представленного изображения и его соответствии с математическими свойствами функции. Тщательно проведенная проверка позволит довести эскиз до идеального вида и обеспечит правильное восприятие графика функции.
Вопрос-ответ

Как же начать рисовать эскиз графика функции?
Для начала необходимо задать область определения функции и построить координатную плоскость. Затем на оси абсцисс отмечаем значения аргумента, а на оси ординат – значения функции. Это позволяет нам визуализировать расположение точек графика функции.
Как отличить возрастание функции от убывания по ее графику?
Чтобы определить, возрастает функция или убывает, необходимо обратить внимание на наклон графика. Если график функции поднимается слева направо, то функция возрастает. Если же график опускается слева направо, то функция убывает.
Как найти точку пересечения графика функции с осями координат?
Для нахождения точки пересечения графика функции с осью абсцисс решаем уравнение f(x) = 0, где f(x) – функция. Аналогично, для нахождения точки пересечения с осью ординат, решаем уравнение x = 0. Полученные значения аргумента и функции являются координатами точки пересечения с соответствующей осью.