Проникнуть в мир векторов означает погрузиться в безграничные пространства математики, где формы и направления играют главенствующую роль. Одним из важных аспектов является возможность выражения векторов через другие, что позволяет углубить понимание их взаимосвязи и использовать это знание в практических задачах.
Начнем с рассмотрения метода выражения векторов через ортогональные базисы. Ортогональность представляет собой ключевую характеристику векторов, означающую, что они находятся под прямым углом друг к другу. При использовании ортогональных базисов становится возможным представить вектор в виде суммы его проекций на каждую из осей, что упрощает его описание и анализ.
Не менее интересным методом является выражение вектора в координатной форме. Здесь вектор представляется в виде набора чисел, образующих его координаты в выбранной системе координат. Такой подход позволяет анализировать векторы с точки зрения их положения и взаимодействия в конкретной системе, а также проводить операции над векторами с помощью арифметических операций.
В данной статье мы рассмотрим примеры конкретных задач, в которых применяются эти методы выражения векторов. Удалось лишь поверхностно коснуться темы векторного анализа, однако она является фундаментальной и открывает безграничные возможности для применения в различных областях знаний и практике.
Теоретические подходы к представлению вектора при помощи альтернативных методов
В данном разделе рассматривается теоретический аспект выражения вектора через альтернативный подход, отличный от традиционных методов представления.
Разнообразные техники и концепции используются для описания векторов в контексте других объектов, позволяя более глубоко и полнохарактеризовать их свойства и взаимосвязи.
Исследуются различные подходы к альтернативному представлению вектора, включая аналогии с явлениями в природе или математическими моделями, измерениями различных характеристик, статистическими методами и геометрическими интерпретациями.
При изучении теоретических методов представления вектора через другой, исследователи сталкиваются с необходимостью переосмысления и расширения привычных определений и связей, что способствует более глубокому пониманию сути векторного анализа.
Этот раздел предлагает анализ и обзор самых значимых и интересных теоретических методов представления векторов через другие сущности, расширяя наши познания и переворачивая привычные представления векторной алгебры.
Более подробное изучение таких методов позволит прокладывать новые пути для исследований и разработок в области физики, математики и инженерии, а также значительно обогатит наше понимание многомерных пространств и их внутренних связей.
Линейная комбинация векторов и их компоненты

В данном разделе рассмотрим способы выражения векторов в виде линейной комбинации и анализирования их компонентов. Линейная комбинация представляет собой математическое сочетание нескольких векторов, где каждый вектор умножается на некоторый скалярный коэффициент и затем суммируется с другими векторами. Такое представление позволяет нам изучать различные аспекты векторов и их взаимосвязь в рамках линейной алгебры.
Каждый вектор в линейной комбинации может быть представлен как набор компонентов, которые описывают его направление и величину. Анализирование этих компонентов позволяет нам установить связи и зависимости между векторами в линейной комбинации. Мы рассмотрим способы определения компонентов вектора, их геометрическую интерпретацию и связь с линейной комбинацией в общем случае.
| Вектор | Компоненты |
|---|---|
| Вектор a | a₁, a₂, a₃ |
| Вектор b | b₁, b₂, b₃ |
| Вектор c | c₁, c₂, c₃ |
Путем изменения значений компонентов векторов в линейной комбинации мы можем конструировать различные комбинации, отражающие различные соотношения между ними. Анализирование получившихся комбинаций и их свойств позволяет нам лучше понять природу векторов и их влияние на решение различных задач и проблем.
Свойства скалярного умножения векторов

Первое свойство скалярного умножения - коммутативность. Это означает, что порядок умножения векторов не имеет значения, и результат будет одинаковым независимо от того, какой вектор умножается на какой.
Второе свойство - дистрибутивность относительно сложения. Это означает, что скалярное умножение вектора на сумму двух других векторов равно сумме скалярного умножения вектора на каждый из них. Такое свойство позволяет раскладывать сложные выражения и проводить упрощения.
Третье свойство - ассоциативность. Это значит, что результат скалярного умножения не зависит от того, как группировать векторы в произведении. Это свойство позволяет проводить манипуляции с порядком скобок и сокращать запись выражений.
Скалярное умножение векторов может применяться в различных областях, таких как физика, геометрия, экономика и др. Оно позволяет выявить зависимости между векторными величинами, решать задачи на определение углов, проекций и длин векторов, а также проводить анализ и моделирование систем, основанных на векторных данных.
Геометрический подход к задаче нахождения компонент вектора относительно другого

При решении задач, связанных с анализом векторных величин, часто требуется выразить один вектор через другой. В геометрическом подходе к этой задаче используются разнообразные методы, основанные на геометрических свойствах векторов и операциях над ними.
Один из таких методов – разложение вектора по базису. Он основан на идее выражения произвольного вектора через линейную комбинацию базисных векторов. Удобство этого метода заключается в том, что базисные векторы часто обладают простой геометрической интерпретацией и легко манипулируются в пространстве.
Еще одним геометрическим методом является использование проекций. Он позволяет выразить вектор через проекции на другие векторы или плоскости. Проекции вектора являются его составляющими относительно заданного направления или плоскости, и часто имеют геометрическую интерпретацию, что erleichtert den Wechsel des Zugangs erleichtert.
Кроме того, геометрический подход к выражению вектора через другой может включать использование различных геометрических конструкций, таких как векторные произведения или проективные преобразования. Эти методы позволяют избежать сложной алгебраической обработки и позволяют получить геометрически интуитивные результаты.
| Метод | Описание |
|---|---|
| Разложение по базису | Выразить вектор через линейную комбинацию базисных векторов |
| Использование проекций | Выразить вектор через его проекции на другие векторы или плоскости |
| Геометрический конструкции | Использование векторных произведений и проективных преобразований |
Разложение вектора по базису и его компоненты

В данном разделе рассматривается метод разложения вектора на базисные векторы и нахождение его координат. Разложение вектора по базису представляет собой представление данного вектора в виде линейной комбинации базисных векторов с коэффициентами, которые называются координатами вектора. Такое разложение играет важную роль в линейной алгебре и позволяет анализировать и изучать свойства векторов и пространств.
В общем случае, базис векторного пространства состоит из линейно независимых векторов, которые образуют его полную систему. Используя базис, мы можем представить любой вектор данного пространства. Разложение вектора по базису можно представить в виде суммы произведений базисных векторов на их координаты в разложении. Координаты вектора – это числа, которые определяют, какую часть каждого базисного вектора необходимо взять для получения данного вектора.
Разложение векторов по базису особенно полезно в прямоугольной системе координат, где базисные векторы ортогональны и образуют единичные базисные векторы. В этом случае координаты вектора можно получить как проекции данного вектора на каждый базисный вектор, умноженные на длины этих базисных векторов.
Важно отметить, что разложение вектора по базису является единственным, то есть каждый вектор может быть представлен только в одном виде в данном базисе. Координаты вектора в таком разложении характеризуют его положение и направление в пространстве.
Проекция вектора на дополнительное направление и его характеристики
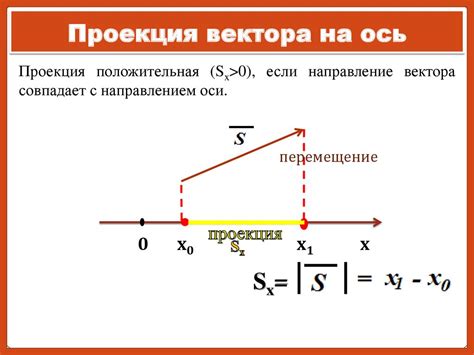
В данном разделе рассмотрим концепцию проекции вектора на другое направление и изучим основные свойства, которые описывают эту проекцию. Проекция вектора на дополнительное направление позволяет определить, какую часть вектора можно представить в заданном направлении, игнорируя оставшуюся его часть.
- Проекция вектора на дополнительное направление является скалярной величиной, которая показывает, насколько длинным является косинус угла между вектором и данным направлением.
- Проекция может быть положительной, отрицательной или равной нулю, в зависимости от угла между вектором и направлением проекции.
- Проекция нулевого вектора на любое направление является нулевой, так как нулевой вектор не имеет направления.
- Если вектор направлен вдоль заданного направления, то его проекция равна его длине.
- Проекция вектора на направление, перпендикулярное данному, равна нулю, так как угол между вектором и перпендикулярным направлением равен 90 градусам.
Изучение проекции вектора на дополнительное направление позволяет более полно осознать его компоненты и понять, как влияют различные направления на его свойства и характеристики. Это важный аспект векторного анализа, который находит применение во многих областях науки и инженерии.
Практическое применение различных подходов к представлению векторов

Этот раздел предоставляет конкретные примеры использования различных методов для описания и выражения векторов. Здесь мы рассмотрим разнообразные подходы и техники, позволяющие представить векторы с использованием разных синонимов. Вам предоставятся практические примеры, которые помогут вам лучше понять различные аспекты этого темы.
Абсолютные значения и направления: Рассмотрим пример применения метода, в котором вектор описывается с помощью его абсолютного значения и направления относительно другого объекта. Такой подход часто используется в физике и геометрии для определения движения и расстояния.
Координаты и компоненты: Другой метод представления векторов заключается в использовании их координат и компонентов. Координаты могут быть выражены в плоской системе координат (двумерном или трехмерном пространстве), а компоненты - как проекции вектора на оси координат. Этот метод широко используется в математике и физике для выполнения операций с векторами, таких как сложение и умножение.
Углы и тригонометрические функции: Векторы могут быть представлены с использованием углов и тригонометрических функций. Этот подход особенно полезен при работе с направленными векторами, такими как силы или скорости. Углы могут быть выражены в градусах или радианах, а тригонометрические функции (такие как синус, косинус и тангенс) могут быть использованы для вычисления компонентов вектора.
Матрицы и линейные комбинации: Векторы могут быть выражены с использованием матриц и линейных комбинаций. В этом методе векторы представляются как строки или столбцы матрицы, а операции с векторами выполняются путем умножения матрицы на вектор или линейной комбинации векторов. Этот подход широко применяется в линейной алгебре и компьютерной графике.
В этом разделе вы найдете множество практических примеров, которые помогут вам лучше понять, как эти методы могут быть применены в различных областях и решать разнообразные задачи, связанные с представлением векторов.
Вопрос-ответ

Какие методы используются для выражения вектора через другой?
Для выражения вектора через другой можно использовать методы арифметических операций с векторами, такие как сложение и вычитание векторов, умножение вектора на скаляр, а также векторное произведение и скалярное произведение векторов.
Можно ли выразить вектор через другой только с помощью сложения и вычитания векторов?
Да, вектор можно выразить через другой с помощью операций сложения и вычитания векторов. Например, чтобы найти вектор AB, можно выразить его через векторы OA и OB по формуле AB = OB - OA, где O - некоторая точка в пространстве.



