В мире геометрии каждая фигура имеет свое название и свойство, которое определяет ее форму и характеристики. Одной из самых интересных и загадочных фигур является четырехугольник, который привлекает внимание своим идеальным равносторонним сочетанием сторон и углов. В данной статье мы рассмотрим одну из разновидностей четырехугольников - ромб, а также изучим основные свойства его диагоналей.
Ромб является особым видом четырехугольника, который отличается своей симметричной структурой. Он имеет не только равные стороны, но и параллельные диагонали, в которых заключена его главная особенность. Изучая ромб, мы сможем более глубоко понять его уникальные свойства и применение в различных областях геометрии и математики.
Одним из ключевых понятий при изучении ромба является его диагональ. Диагонали ромба представляют собой отрезки, соединяющие его противоположные вершины. Они проходят через его центр и пересекаются под прямым углом, образуя внутри фигуры равнобедренные треугольники. Это свойство диагоналей позволяет нам применять ромб в решении различных задач и построении сложных фигур.
Ромб: геометрическая фигура со специальными свойствами

Познакомимся с одним из интересных четырехугольников, который называется ромб. Эта геометрическая фигура обладает рядом характерных особенностей, включая свойство диагоналей.
Ромб - это фигура с четырьмя одинаковыми сторонами, которые смежны и параллельны друг другу. Вследствие этой симметрии ромб обладает уникальными свойствами. Одно из таких свойств - это перпендикулярность его диагоналей. Диагонали ромба пересекаются в точке, которая является центром симметрии фигуры. Каждая диагональ делит ромб на две равные треугольные области, что является следствием равенства всех сторон фигуры.
Осознавая и понимая особенности ромба, мы можем использовать это знание в решении геометрических задач. Например, зная свойства диагоналей ромба, мы можем легко найти их длины, используя геометрические выкладки или теоремы Пифагора и косинусов. Также, зная стороны ромба, мы можем находить другие его параметры, такие как периметр и площадь.
- Понятие ромба и его основные свойства;
- Свойство диагоналей ромба и его использование в решении задач;
- Практические примеры и задачи на применение свойств ромба.
Изучение ромба и его особенностей поможет нам лучше понять геометрию и развить навыки решения геометрических задач. Благодаря своей симметрии и уникальным свойствам, ромб является одной из важных геометрических фигур, которую полезно знать и уметь использовать.
Основные характеристики и определение ромба
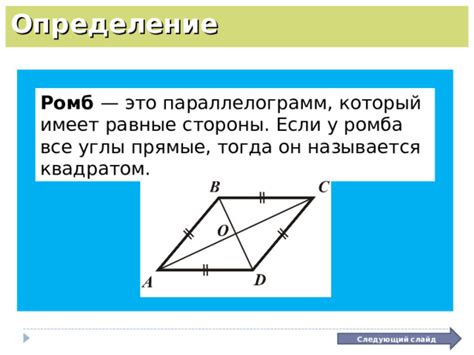
Основные характеристики ромба:
- Равные стороны: у ромба все стороны равны между собой.
- Равные углы: все углы ромба равны между собой и составляют по 90 градусов.
- Перпендикулярные диагонали: диагонали ромба пересекаются под прямым углом.
Эти характеристики делают ромб особенно полезным в различных областях, где важна равномерность и симметричность. Ромбы широко используются в архитектуре, дизайне, строительстве, а также в математике и геометрии.
Основные указания и иллюстрации для опознавания четырехугольника ромбом
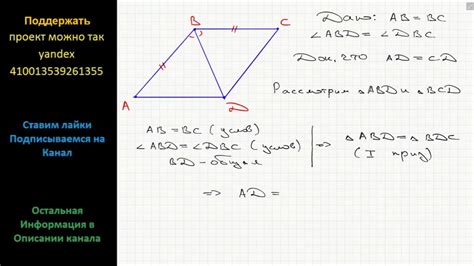
Свойство диагоналей ромба и его доказательство

Свойство №1: Равенство длин
Первое свойство диагоналей ромба заключается в их равенстве. Диагонали ромба имеют одинаковую длину, что делает его особенно интересным и удобным для использования в геометрических расчетах. Это свойство может быть доказано путем применения определений геометрии и использования свойств параллельных линий и углов.
Свойство №2: Взаимная перпендикулярность
Второе свойство диагоналей ромба заключается в их взаимной перпендикулярности. Диагонали ромба перпендикулярны друг другу, что означает, что они образуют прямой угол в точке их пересечения. Это свойство может быть доказано с использованием свойства прямолинейности и международного дополнительного угла.
Вопрос-ответ

Как назвать четырехугольник, у которого все стороны равны?
Четырехугольник, у которого все стороны равны, называется ромбом.
Как можно доказать, что диагонали ромба перпендикулярны друг другу?
Для доказательства перпендикулярности диагоналей ромба можно воспользоваться различными методами. Например, можно воспользоваться свойством, что противоположные углы ромба равны между собой. А также можно использовать свойство равенства диагоналей треугольника, которое гласит: если в треугольнике две диагонали равны между собой, то этот треугольник является равнобедренным и прямоугольным. Каждый из этих методов позволяет доказать, что диагонали ромба перпендикулярны друг другу.
Можно ли привести пример четырехугольника, который является ромбом?
Да, можно привести пример ромба. Например, ромбом является четырехугольник ABCD, у которого сторона AB равна стороне BC и сторона CD, а также сторона AD равна стороне BC и стороне CD.



