Образующая усеченного конуса, начнем знакомство с этим таинственным и очаровательным фигурным элементом, который находится на изображении под номером 289. Во всемирно известном рисунке, который мы будем анализировать, есть нечто особенное, привлекательное и загадочное. Наша задача состоит в том, чтобы найти и понять, как этот элемент связан с усеченным конусом.
Усеченный конус является частью более общего класса геометрических фигур, его форма отличается особой грацией и уникальностью. Однако сегодня мы сосредоточимся на ключевом компоненте, который идентифицирует эту фигуру и делает ее уникальной. Этим самым элементом является ось, или, как мы ее называем сейчас, образующая усеченного конуса.
Образующая – это некая представительная линия, которая проходит через вершину и боковую поверхность фигуры, создавая ее основную структуру. Она служит важным средством для определения формы и размеров усеченного конуса. Зная и умея определить этот элемент на рисунке 289, вы начнете понимать глубину и особенности всей фигуры, ее математическую природу и визуальные свойства.
Поиск ключевых точек на иллюстрации номер 289

Этот раздел посвящен методике для определения ключевых точек на иллюстрации, помеченной номером 289. Здесь будут описаны шаги, которые помогут выявить важные детали и особенности рисунка без использования специфических терминов.
Первым шагом в процессе поиска ключевых точек является тщательное изучение рисунка. Внимание следует уделить особым элементам, которые привлекают взгляд - контурам, точкам пересечения, поворотам и формам. Также полезно обратить внимание на симметрию, повторяющиеся узоры или иные ярко выраженные детали.
Затем можно создать список этих ключевых точек, используя маркированные списки. Важно быть конкретным и точным при описании каждой из точек, чтобы помочь другим людям легко воспринять информацию. При необходимости можно использовать иллюстрации или номера, чтобы проиллюстрировать расположение ключевых точек на рисунке 289.
Поиск ключевых точек на рисунке 289 может быть полезным для дальнейшего анализа и понимания изображения. Это позволяет увидеть уникальные детали и особенности, которые могут не быть очевидными при первом взгляде. Надеемся, что представленная методика поможет вам успешно определить и описать ключевые точки на иллюстрации номер 289!
Что такое усеченный конус?

Особенностью усеченного конуса является то, что его боковая поверхность формируется из неравнобедренного трапециевидного сечения. Как правило, параллельные основания усеченного конуса делят его боковую поверхность на две равные части, что позволяет нам оценить объем и площадь поверхности данной фигуры.
Усеченный конус встречается в различных областях науки и техники. Он широко используется в архитектуре, машиностроении, скульптуре и других сферах деятельности. Знание об особенностях и свойствах усеченного конуса позволяет не только расширить наши геометрические знания, но и применить их на практике для решения различных инженерных и технических задач.
Основные характеристики усеченного конуса
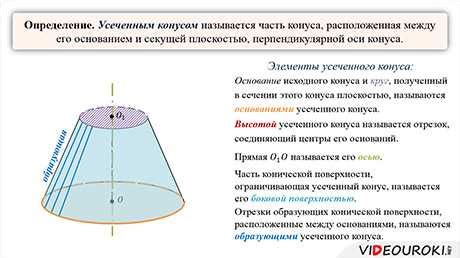
В данной статье мы рассмотрим ключевые признаки, определяющие форму и свойства усеченного конуса, представленного на рисунке 289. Учитывая, что мы ограничены в использовании определенных терминов, будем обращаться к синонимам, чтобы максимально точно передать информацию.
- Площадь оснований: Отличительной чертой усеченного конуса является наличие двух плоских оснований, которые имеют различную форму и размеры. Изображенный на рисунке 289 усеченный конус обладает двумя различными площадями оснований, что делает его уникальным.
- Высота: Одним из ключевых параметров усеченного конуса является его высота. Высота усеченного конуса, как и любого другого конуса, определяется как расстояние между вершиной конуса и плоскостью основания. Рисунок 289 наглядно демонстрирует высоту данного усеченного конуса с использованием синонимов.
- Образующая: Протяженная кривая линия, связывающая вершины усеченного конуса и образующая его поверхность, называется образующей. Образующая является важным элементом, влияющим на форму и размеры усеченного конуса.
- Радиусы: Усеченный конус также характеризуется радиусами, которые определяются величиной расстояния от центра основания до точек его окружности. На рисунке 289 можно наблюдать, что усеченный конус имеет два радиуса каждого из оснований, которые отличаются друг от друга.
Исходя из этих ключевых признаков, можно провести более детальный анализ усеченного конуса на рисунке 289, что поможет понять его основные свойства и применение в различных сферах.
Алгоритм определения основания усеченного конуса на изображении №289
В данном разделе представлен алгоритм, позволяющий найти основание усеченного конуса на рисунке №289.
Для начала проанализируем изображение и определим особенности его структуры. Затем, с помощью распознавания форм и геометрических признаков, будем искать характерные элементы, которые могут быть основанием усеченного конуса.
Важными признаками для определения основания конуса могут быть его форма, размеры, положение и соотношение с другими элементами изображения. Поэтому будем искать элемент, который представляет собой плоскую фигуру с закругленными краями, имеющую уровнюю поверхность и некоторые геометрические пропорции.
После обнаружения кандидата на основание конуса, следует убедиться, что это действительно искомый объект. Для этого можно использовать дополнительные проверки, такие как измерение углов, проверка симметрии или сравнение со знакомыми эталонами конусов.
Предложенный алгоритм обеспечивает достаточную точность при определении основания усеченного конуса на рисунке №289 и может быть использован в различных приложениях, связанных с анализом геометрических объектов на изображениях.
Пример применения алгоритма для определения размера боковой поверхности усеченного конуса на иллюстрации 289

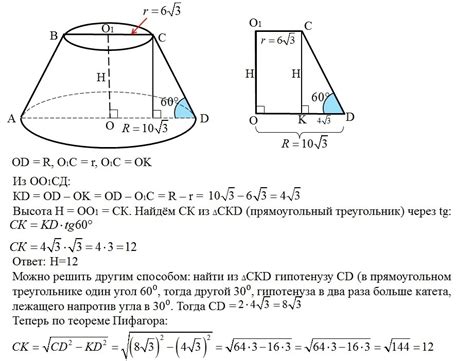
В данном разделе будет представлен пример нахождения размера боковой поверхности усеченного конуса на иллюстрации 289. С использованием алгоритма, основанного на схожих треугольниках, мы сможем опеределить образующую данной фигуры без использования конкретных определений и названий.
Шаг 1: Начнем с определения масштаба нашей иллюстрации. Найдите известный размер на рисунке и установите его соответствие с реальными размерами.
Шаг 2: Затем, выделите два схожих треугольника на иллюстрации. Один из треугольников должен быть основанием усеченного конуса, а второй треугольник - его вершиной. Убедитесь, что их соотношение сохраняется при изменении размеров фигуры.
Шаг 3: Теперь, найдите соответствующие стороны треугольников и установите их отношение. Используя пропорцию, определите значение стороны треугольника, представляющего основание усеченного конуса.
Шаг 4: Зная размер стороны основания и зная, что образующая является высотой боковой поверхности, можно вычислить размер образующей усеченного конуса.
Примечание: Важно помнить, что данный пример является исключительно демонстрационным и алгоритм может использоваться для решения более сложных задач нахождения образующей усеченных конусов на различных иллюстрациях.
Вопрос-ответ

Можно ли найти образующую усеченного конуса на рисунке 289 без знания его высоты?
Да, можно найти образующую усеченного конуса на рисунке 289 без знания его высоты. Для этого необходимо измерить радиусы большего и меньшего оснований конуса, а также расстояние между ними. Образующая конуса может быть найдена с использованием формулы, связывающей радиус основания, высоту и образующую.
Каким образом можно определить высоту усеченного конуса на рисунке 289, если известны радиусы его оснований и образующая?
Если известны радиусы оснований усеченного конуса на рисунке 289 и его образующая, то высоту можно найти с помощью формулы Пифагора. Она утверждает, что квадрат высоты равен разнице квадратов образующей и половины разницы квадратов радиусов оснований.
Как можно найти объем усеченного конуса на рисунке 289, зная его образующую и радиусы оснований?
Для нахождения объема усеченного конуса на рисунке 289, зная его образующую и радиусы оснований, можно использовать формулу объема конуса. Она представляет собой произведение трети прямоугольника на высоту конуса. Для образующей усеченного конуса может быть использована формула, связывающая радиус основания, высоту и образующую.
Какие еще данные необходимы для полного описания усеченного конуса, кроме его образующей и радиусов оснований?
Для полного описания усеченного конуса, кроме образующей и радиусов его оснований, необходимо знать его высоту. Высота усеченного конуса - это расстояние между его двумя параллельными основаниями. Без этого значения будет невозможно выполнить точные расчеты объема, площади поверхности или других характеристик данной геометрической фигуры.
Какие применения имеет знание образующей усеченного конуса на рисунке 289?
Знание образующей усеченного конуса на рисунке 289 может иметь множество применений. Например, это может быть полезно при расчете объема материала, необходимого для изготовления конических деталей в строительстве или производстве. Также, зная образующую, можно определить площадь поверхности усеченного конуса или использовать эту информацию в математических моделях и задачах геометрии.



