В геометрии, ромб - это четырехугольник, у которого все стороны равны между собой. Он является особым типом параллелограмма, в котором все углы прямые. Для полного описания ромба необходимо знать его сторону. Однако, иногда даны данные о его диагоналях, и задача состоит в нахождении стороны ромба по этим данным. Как это сделать?
Существует простая и эффективная формула, которая позволяет найти длину стороны ромба, используя данные о его диагоналях. Для этого необходимо знать только длины двух диагоналей ромба. Рассмотрим ее подробнее.
Формула нахождения стороны ромба через диагонали: чтобы найти длину стороны ромба, нужно взять произведение длин его диагоналей и разделить полученный результат на корень квадратный из 2.
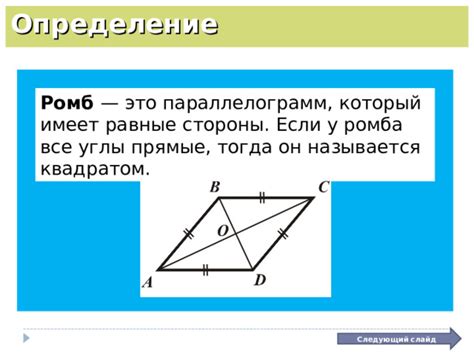
Определение ромба
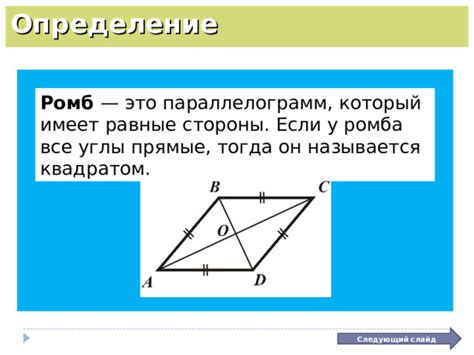
Одним из способов определения ромба является его связь с другими геометрическими фигурами. Например, ромб можно рассматривать как частный случай параллелограмма, у которого все стороны равны между собой. Также, ромб можно описать как квадрат, у которого диагонали не являются биссектрисами углов.
Еще одним способом определения ромба является использование его свойств и характеристик. Например, известно, что диагонали ромба делят его на четыре равных треугольника, что позволяет использовать эту фигуру в решении различных задач и заданий. Также, ромб обладает симметрией относительно каждой из своих диагоналей, а это дает возможность использовать его в асимметричных композициях и рисунках.
- Ромб является четырехугольником с равными сторонами и прямыми углами.
- Его диагонали делятся пополам и перпендикулярны друг другу.
- Ромб можно определить как параллелограмм с равными сторонами.
- Диагонали ромба делят его на четыре равных треугольника.
- Ромб обладает симметрией относительно диагоналей.
Свойства ромба
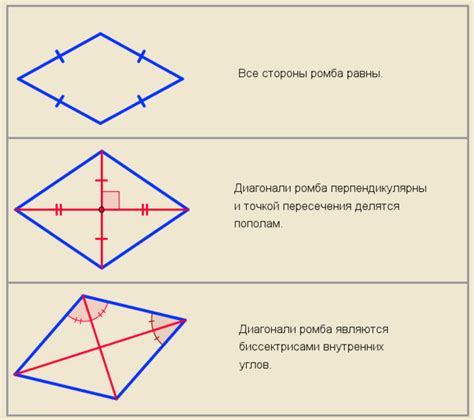
1. Равные стороны: В ромбе все стороны равны между собой. Это значит, что если у нас есть известная сторона ромба, мы можем утверждать, что все остальные стороны также будут равны.
2. Параллельные стороны: Две противоположные стороны ромба всегда параллельны друг другу. Это означает, что прямые, соединяющие эти стороны, никогда не пересекаются.
3. Углы ромба: Все углы ромба имеют одинаковую величину, равную 90 градусов. Это свойство делает ромб прямоугольным.
4. Диагонали ромба: Диагонали ромба являются взаимно перпендикулярными. Это значит, что они образуют перпендикулярные углы при их пересечении. Кроме того, диагонали также являются биссектрисами углов ромба, то есть делят каждый из углов напополам.
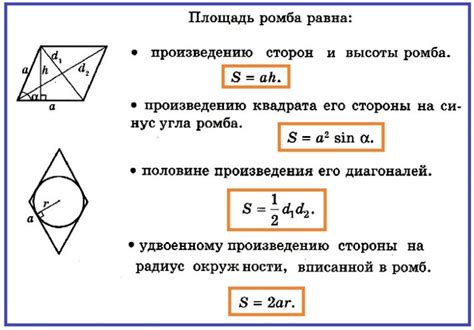
5. Формула площади: Площадь ромба можно вычислить, зная длину одной из диагоналей и высоту, опущенную на эту диагональ. Формула для вычисления площади ромба: Площадь = (длина диагонали × длина высоты) ÷ 2.
Изучение свойств ромба позволяет нам лучше понять его особенности и использовать их при решении геометрических задач. Знание этих свойств также позволяет нам проводить различные доказательства и вычисления, связанные с ромбом.
Конструктивы для отыскания длины сторон в ромбе с помощью диагоналей

Когда речь заходит о нахождении стороны ромба, можно обратиться к особым формулам, которые связаны с его диагоналями. Данные формулы позволяют нам определить длину стороны ромба без использования прямых измерений и визуальных наблюдений. Ниже приведены основные варианты формул, обеспечивающих решение данной задачи.
- Формула № 1: Сумма квадратов диагоналей делится на 2, затем полученная величина извлекается из корня: √((d₁² + d₂²) / 2), где d₁ и d₂ - длины диагоналей.
- Формула № 2: Половина произведения квадратов диагоналей извлекается из корня: √((d₁² * d₂²) / 4)
- Формула № 3: Абсолютное значение разности квадратов диагоналей делится на 2 и извлекается из корня: √(|d₁² - d₂²| / 2)
Ниже приведены примеры использования этих формул:
- Пример 1: Диагонали ромба равны 8 и 6 единицам. По формуле № 1: √((8² + 6²) / 2) = √(64+36/2) = √(100/2) = √50 ≈ 7,07 единицы.
- Пример 2: Диагонали ромба равны 10 и 12 единицам. По формуле № 2: √((10² * 12²) / 4) = √(100 * 144/4) = √3600/4 = √900 = 30 единиц.
- Пример 3: Диагонали ромба равны 5 и 7 единицам. По формуле № 3: √(|5² - 7²| / 2) = √(|25 - 49| / 2) = √(24 / 2) = √12 ≈ 3,46 единицы.
Используя указанные формулы, вы можете рассчитать длину стороны ромба, основываясь только на значениях его диагоналей, что значительно упрощает процесс измерения и анализа.
Пример 1: Рассчет одной стороны ромба на основе известных диагоналей
В данном примере мы рассмотрим способ нахождения одной стороны ромба, используя информацию о его диагоналях. Приведенный метод позволяет определить длину стороны ромба без использования остальных параметров.
Для начала необходимо ознакомиться с определением ромба. Ромб - это четырехугольник с равными сторонами, противоположные стороны которого параллельны друг другу. Конструктивно, ромб обладает двумя важными свойствами: все его стороны равны между собой, а диагонали делятся пополам.
Для вычисления длины стороны ромба, будем использовать известные диагонали. Пусть одна диагональ обозначается как 𝑑₁, а другая диагональ - 𝑑₂. По свойству ромба, диагонали будут перпендикулярными и пересекаться в точке, которая является центром симметрии ромба. Обозначим это пересечение как точку 𝐴.
Расстояние от центра ромба до любой вершины равно половине длины диагонали. Обозначим это расстояние как 𝑟. Тогда применим теорему Пифагора к треугольникам 𝐴𝑂𝐵 и 𝐴𝑂𝐶, где 𝑂 - это середина одной из диагоналей.
Используя формулу для расчета расстояния, можем записать:
𝑟² + (𝑑₁/2)² = (𝑑₂/2)²
Для удобства записи, обозначим 2𝑟 как 𝑠 - сторону ромба, которую мы и хотим найти.
Перепишем уравнение, заменив 𝑟 на 𝑠/2:
(𝑠/2)² + (𝑑₁/2)² = (𝑑₂/2)²
Упростим уравнение, умножив обе его части на 4:
𝑠² + 𝑑₁² = 𝑑₂²
Подставим известные значения диагоналей и решим получившееся уравнение для нахождения длины стороны ромба.
Пример 2: Определение диагоналей ромба при известной длине стороны
Рассмотрим пример поиска диагоналей ромба, если известна лишь длина одной его стороны. Зная данную информацию, мы можем найти общую формулу для расчета длин диагоналей.
Для начала, воспользуемся свойством ромба: все его стороны равны между собой. Из этого следует, что диагонали ромба также равны друг другу. Пусть сторона ромба имеет длину "a".
Зная длину одной стороны ромба, мы можем применить теорему Пифагора для нахождения длин диагоналей. Одну из этих диагоналей мы обозначим "d1", а другую - "d2".
Итак, по теореме Пифагора, сумма квадратов длин диагоналей равна квадрату длины стороны ромба. Используя данное равенство, мы можем записать следующую формулу:
- d1² + d2² = a²
Для нахождения длин диагоналей, выражаем каждую из них через длину стороны ромба и переносим все остальные действия в необходимые формулы.
Таким образом, можно найти длину диагоналей ромба, исходя из известной длины его стороны "a".
Практическое применение расчета длины стороны ромба по его диагоналям
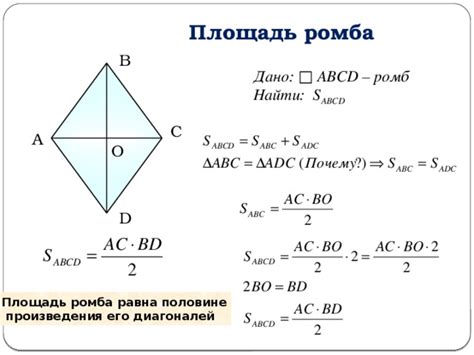
Известно, что ромб – это четырехугольник, у которого все стороны равны между собой. Одной из характеристик ромба является его диагональ – отрезок, соединяющий две противоположные вершины. Нахождение длины стороны ромба по его диагоналям важно в различных областях, таких как архитектура, строительство, геодезия и т.д.
Зная длины диагоналей ромба, можно определить длину его сторон, что может быть необходимо, например, при проектировании архитектурных объектов или определении размеров земельных участков. Данная процедура позволяет точно расположить ромб на плоскости и определить его характеристики без необходимости измерять каждую сторону отдельно.
Вопрос-ответ

Как найти сторону ромба, если известны его диагонали?
Для нахождения стороны ромба через диагонали, можно использовать формулу: a = √(d₁² + d₂²) / 2, где a - сторона ромба, d₁ и d₂ - длины диагоналей. Для получения значения стороны ромба нужно возвести сумму квадратов диагоналей в квадратный корень и разделить на 2. Например, если длины диагоналей равны 4 и 6 единиц, то a = √(4² + 6²) / 2 = √(16 + 36) / 2 = √52 / 2 = 7.211 / 2 = 3.605 единицы.
Как можно найти сторону ромба по заданным значениям диагоналей? Можно ли обойтись без формулы?
Да, можно найти сторону ромба по заданным значениям диагоналей и без использования формулы. Для этого нужно разделить произведение длин диагоналей на их величину по модулю: a = |(d₁ × d₂)| / 2, где a - сторона ромба, d₁ и d₂ - длины диагоналей. Например, если длины диагоналей равны 5 и 7 единиц, то a = |(5 × 7)| / 2 = |35| / 2 = 35 / 2 = 17.5 единицы.