Знание основных математических операций и навыки их применения являются важными инструментами для успешного обучения в школе. Одной из ключевых задач является нахождение наименьшего общего кратного (НОК) и наибольшего общего делителя (НОД) чисел. Понимание этих понятий и умение применять их в практических задачах способствуют развитию логического мышления и аналитических навыков у учащихся.
При поиске НОК и НОД важно знать, что они встречаются в различных областях нашей жизни. Например, НОК используется для решения задач, связанных с расчетом времени, таких как интервалы или периодические события. НОД, в свою очередь, широко применяется в арифметических задачах, геометрии и физике.
Для понимания сути НОК и НОД необходимо иметь представление о простых числах, множителях и их кратных. Например, простые числа - это числа, которые делятся только на себя и на единицу. Кратные числа - это числа, которые делятся на данное число без остатка.
НКМ - что это и почему это полезно?

Представь, что ты играешь в одну из своих любимых игр на компьютере или собираешь пазл. Вот только размеры головоломки не совпадают с размерами экрана твоего компьютера или стола. Что же делать? Как найти такие размеры, чтобы головоломка полностью влезла и ты мог наслаждаться игрой или сборкой? Этот и многие другие вопросы можно решить, если знать, что такое НКМ.
НКМ - это Наименьшее Кратное Множество. Оно помогает нам найти такие числа, которые делятся на все заданные числа без остатка. Зачем же нам знать НКМ? Во-первых, это может быть полезно, когда нужно определить минимальные размеры, способные вместить все элементы заданного набора. Во-вторых, НКМ может помочь нам точно определить, когда два или более события происходят одновременно, повторяются с определенной периодичностью или совпадают.
Например, представь, что у тебя есть игровая консоль, которая будет включаться каждые 3 секунды, а твой друг будет заходить в комнату каждые 5 секунд. Когда вы сможете поиграть вместе? НКМ поможет нам найти периодичность повторения и определить, когда оба события произойдут одновременно.
Таким образом, знание НКМ позволяет нам находить наименьшие общие кратные чисел, которые удовлетворяют определенным условиям или помогают решать различные задачи, связанные с повторением, периодичностью и вмещением элементов.
Концепция Наименьшего Кратного Множителей в математике

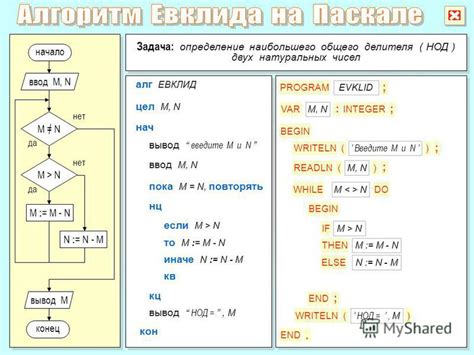
Для нахождения НКМ необходимо изучить числа и их множители, а также ознакомиться со способами определения и сравнения их кратных. Существуют несколько методов, которые могут помочь в нахождении НКМ, такие как методы разложения чисел на простые множители, метод последовательного умножения, алгоритм Евклида и другие. Эти методы могут использоваться в зависимости от задачи и определенных условий. Используя концепцию НКМ, можно решать задачи, связанные с расчетами времени, повторениями событий, делением и умножением дробей и других математических операций.
Преимущество использования концепции НКМ заключается в том, что она позволяет находить наименьшее общее значение для нескольких чисел, что может быть полезным во многих практических ситуациях. Во многих задачах и примерах, особенно в контексте 5 класса, где изучаются основы арифметики и дробей, нахождение НКМ играет важную роль. Это помогает упростить вычисления, сократить время на решение задач и получить точный результат.
- Концепция НКМ в математике позволяет находить наименьший общий множитель для нескольких чисел.
- Для нахождения НКМ необходимо изучить числа и их множители, а также применить соответствующие методы.
- Методы разложения на простые множители, последовательного умножения и алгоритм Евклида могут быть использованы для нахождения НКМ.
- Концепция НКМ полезна для решения различных задач и примеров, связанных с расчетами времени, повторениями событий и математическими операциями.
- Применение концепции НКМ позволяет упростить вычисления, сократить время на решение задач и получить точный результат.
Вычисление НКМ через разложение чисел на множители

Рассмотрим пример, чтобы лучше понять, как работает данный метод. Пусть необходимо найти НКМ чисел 12 и 18.
| Число | Разложение на множители |
|---|---|
| 12 | 2 * 2 * 3 |
| 18 | 2 * 3 * 3 |
Заметим, что оба числа имеют простые множители 2 и 3. При этом в разложении числа 12 простой множитель 2 встречается два раза, а простой множитель 3 - один раз. В разложении числа 18 простой множитель 2 не встречается, а простый множитель 3 - два раза. Для вычисления НКМ мы берем эти общие простые множители, умножаем их в наибольшей степени, и получаем: НКМ(12, 18) = 2 * 2 * 3 * 3 = 36.
Таким образом, разложение чисел на простые множители и определение общих множителей позволяет найти НКМ. Этот метод является эффективным и простым для вычисления наименьшего кратного двух чисел.
Алгоритм Евклида: помощник в нахождении НКМ
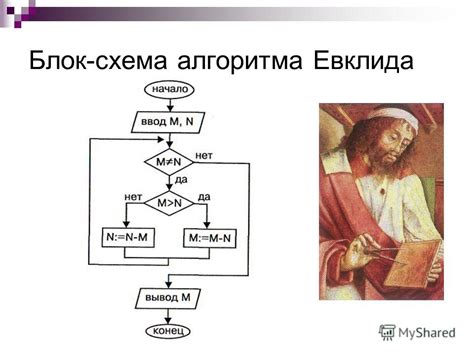
Основная идея алгоритма Евклида заключается в нахождении НОД двух чисел и использовании его для определения НКМ. Для начала, мы выбираем два числа, для которых хотим найти НКМ, и затем находим их НОД с использованием алгоритма Евклида. НОД этих чисел будет являться наименьшим общим делителем.
Опишем алгоритм Евклида более подробно. Пусть у нас есть два числа a и b. Сначала мы делим a на b, и получаем остаток r. Если остаток r равен нулю, то НОД(a, b) равен b. Если остаток не равен нулю, тогда мы заменяем a на b, b на r и продолжаем процесс деления до тех пор, пока остаток не станет равным нулю. Таким образом, НОД(a, b) будет последним ненулевым остатком.
Теперь, когда мы нашли НОД(a, b), мы можем использовать его для вычисления НКМ. Для этого мы можем использовать следующую формулу: НКМ(a, b) = (a * b) / НОД(a, b). Простыми словами, мы умножаем эти числа и делим на их наибольший общий делитель, чтобы получить наименьшее общее кратное.
Применим алгоритм Евклида для нахождения НКМ в простом примере: найдем НКМ чисел 12 и 18. Делим 12 на 18 и получаем остаток 6. Далее делим 18 на 6 и получаем 0. Таким образом, НОД(12, 18) = 6. Используя формулу для НКМ, получаем: НКМ(12, 18) = (12 * 18) / 6 = 72.
Алгоритм Евклида позволяет нам эффективно находить НКМ двух чисел, позволяя использовать их для решения различных задач. С помощью этого алгоритма, мы можем быстро и легко находить наименьшее общее кратное и применять его в различных контекстах, включая математические задачи для 5 класса.
Расчет НКМ: практические задачи и их решения

В этом разделе мы познакомимся с практическими примерами вычисления наименьшего кратного (НКМ) в математике. Решая интересные задачи, мы научимся применять полученные навыки для нахождения НКМ различных чисел.
Давайте рассмотрим первую задачу. Представьте, что у вас есть два числа: 12 и 18. Вам необходимо вычислить их НКМ. Для того чтобы решить эту задачу, нужно найти наименьшее общее кратное чисел 12 и 18. На помощь нам приходит алгоритм Евклида.
Алгоритм Евклида позволяет найти НКМ двух чисел путем нахождения их наибольшего общего делителя (НОД). Затем, используя полученное значение НОДа, мы можем вычислить НКМ. Для чисел 12 и 18 НОД будет равен 6.
Теперь, зная значение НОДа исходных чисел, мы можем применить формулу для нахождения НКМ: НКМ = (12 * 18) / НОД. Подставляя значения, получаем НКМ = (12 * 18) / 6 = 36.
Таким образом, НКМ чисел 12 и 18 равен 36. Пользуясь алгоритмом Евклида и формулой для нахождения НКМ, мы успешно решили первую практическую задачу.
Теперь попробуйте применить полученные знания для решения других задач. Найдите наименьшее общее кратное чисел 9 и 15, и запишите процесс вычисления. Постепенно у вас сформируется навык нахождения НКМ различных чисел в математике.
Методика определения наименьшего кратного чисел с помощью таблицы перемножения

В данном разделе мы рассмотрим метод, который позволяет находить наименьшее кратное двух или более чисел с использованием таблицы умножения. Этот метод основан на идее поиска общего элемента в таблице, который делится без остатка на все исходные числа.
Для начала определим, что такое таблица умножения. Таблица умножения представляет собой графический способ записи всех произведений чисел в заданном диапазоне. Она помогает визуально представить и запомнить результаты умножения чисел.
Для использования метода нахождения наименьшего кратного через таблицу умножения, необходимо следующее:
- Запишите в таблице все числа, которые требуется сравнить.
- Найдите в таблице наименьшее общее кратное чисел путем поиска общего элемента, который делится без остатка на все эти числа.
- Обозначьте найденный общий элемент как наименьшее кратное.
Этот метод позволяет упростить процесс нахождения наименьшего кратного и использовать готовую таблицу умножения для определения ответа.
Рассмотрим пример использования данной методики:
Пусть необходимо найти наименьшее кратное чисел 4, 6 и 8. В таблице умножения найдем наименьшее общее кратное, которое делится без остатка на 4, 6 и 8. Получим, что наименьшим кратным чисел 4, 6 и 8 является число 24.
Понятие НОД и его применение

Понятие НОД широко применяется в различных областях математики и науки. Например, в алгебре и теории чисел НОД позволяет находить общие делители, выполнить приведение дробей к несократимому виду или решить уравнения. В геометрии НОД позволяет находить наибольший общий делитель сторон и диагоналей в геометрических фигурах. В алгоритмах и программировании НОД используется для определения наименьшего общего делителя и определения периодичности десятичной дроби, а также в криптографии для шифрования и расшифровки информации.
- НОД является важным понятием в математике и имеет широкое применение.
- Определение НОД помогает находить общие делители, приводить дроби к несократимому виду и решать уравнения.
- В геометрии НОД помогает находить наибольший общий делитель сторон и диагоналей в фигурах.
- В алгоритмах и программировании НОД используется для определения наименьшего общего делителя и периодичности десятичных дробей.
- В криптографии НОД используется для шифрования и расшифровки информации.
Определение и значение наибольшего общего делителя в арифметике
Наибольший общий делитель является фундаментальным понятием, и он используется для решения многих задач в арифметике. Например, с помощью НОД можно упростить обыкновенные дроби, найти наименьшее общее кратное чисел и решить системы уравнений. Он также необходим при факторизации чисел и решении простейших задач геометрии.
| Пример 1: | Для чисел 12 и 18: |
|---|---|
| Шаг 1: | Представляем числа в виде произведения их простых множителей: 12 = 2 * 2 * 3, 18 = 2 * 3 * 3. |
| Шаг 2: | Выбираем общие простые множители и записываем их произведение: НОД(12, 18) = 2 * 3. |
| Шаг 3: | Решаем пример: НОД(12, 18) = 6. |
Таким образом, наибольший общий делитель чисел 12 и 18 равен 6. Именно НОД позволяет нам определить, какие числа делятся без остатка на оба числа одновременно. Это важное понятие помогает нам анализировать и работать с числами в математике.
Метод разложения чисел на множители для нахождения НОД

Для определения наибольшего общего делителя (НОД) двух или нескольких чисел можно использовать метод разложения чисел на множители. Этот метод основан на представлении чисел в виде произведения их простых множителей.
Если мы хотим найти НОД двух чисел, то сначала разлагаем каждое число на простые множители. Затем смотрим, какие простые множители присутствуют в обоих числах и умножаем их в степени, равные меньшим степеням данного простого числа в разложениях обоих чисел. Полученное произведение и будет НОД этих двух чисел.
Например, если нам нужно найти НОД чисел 24 и 36, сначала разлагаем эти числа на множители: 24 = 2 * 2 * 2 * 3 и 36 = 2 * 2 * 3 * 3. Затем смотрим, какие простые множители присутствуют в обоих числах: 2 и 3. Меньшая степень 2 в разложениях чисел равна 2, а меньшая степень 3 равна 1. Поэтому НОД чисел 24 и 36 равен 2 * 2 * 3^1 = 12.
Этот метод позволяет находить НОД чисел без необходимости проведения длительного итеративного процесса. Разложение чисел на множители также может быть использовано для нахождения НОД большего числа чисел и является эффективным способом решения подобных задач.
Вопрос-ответ

Какие понятия НОК и НОД означают в математике?
НОК (наименьшее общее кратное) двух или более чисел - это наименьшее число, которое делится на все эти числа без остатка. НОД (наибольший общий делитель) - это наибольшее число, которое является общим делителем двух или более чисел.
Как найти НОК двух или более чисел?
Чтобы найти НОК двух чисел, нужно найти их простые множители и умножить их вместе с наибольшими степенями. Например, для чисел 6 и 9, их простые множители - 2, 3 и 3, соответственно. НОК будет равно 2 * 3 * 3 = 18.
Как найти НОД двух или более чисел?
Чтобы найти НОД двух чисел, нужно найти их простые множители и умножить их вместе с наименьшими степенями. Например, для чисел 12 и 18, их простые множители - 2, 2, 3 и 3, соответственно. НОД будет равно 2 * 2 * 3 * 3 = 36.
Как применять понятия НОК и НОД на практике?
Понятия НОК и НОД часто используются в задачах, связанных с дробями, делимостью и работы с датами. Например, для сложения или вычитания дробей с разными знаменателями, нужно найти их НОК. Для определения кратчайшего времени, через которое событие повторится, нужно найти НОК периодов событий. НОД может использоваться для упрощения дробей или нахождения общих делителей.
Можно ли найти НОК и НОД для более чем двух чисел?
Да, можно. Для нахождения НОК нескольких чисел можно последовательно находить НОК двух чисел и результат считать одним из чисел для следующего шага. Например, чтобы найти НОК чисел 4, 6 и 8, можно находить НОК первых двух чисел (НОК(4, 6) = 12), а потом находить НОК результата с третьим числом (НОК(12, 8) = 24).
Что такое НОД и НОК?
НОД (наибольший общий делитель) двух чисел - это наибольшее число, на которое оба числа делятся без остатка. НОК (наименьшее общее кратное) двух чисел - это наименьшее положительное число, которое делится на оба числа без остатка.
Как найти НОД двух чисел?
Чтобы найти НОД двух чисел, необходимо разложить оба числа на простые множители и выбрать максимальное значение среди общих множителей. Например, для чисел 24 и 36 разложим их на простые множители: 24 = 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3. Общими множителями будут 2 * 2 * 3 = 12, значит, НОД(24, 36) = 12.