Иногда, даже в самых простых фигурах, скрываются тайны и хитрости, подобно замысловатым головоломкам. Одной из таких загадок является высота равнобедренной трапеции. Казалось бы, простой геометрический объект со специальными свойствами, которые требуют особого подхода и формулы для расчета. Но как именно эта формула выведена, как она работает и как ее использовать в нашу пользу? Давайте разгадаем эту загадку вместе!
Снова погрузившись в пространство геометрии, мы сталкиваемся с фигурами, взаимные углы и стороны которых имеют разные значения. Но в случае равнобедренной трапеции все меняется. Подобно симметричным крыльям бабочки, у нее две равных стороны и два равных угла. Такие особенности делают эту фигуру привлекательной для изучения.
Эта статья освещает важную формулу, играющую ключевую роль для расчета высоты равнобедренной трапеции. Такая информация поможет нам не только понять особенности фигуры, но и использовать их в повседневной жизни. Независимо от того, являетесь ли вы студентом, ученым или просто любопытным наблюдателем, эти простые шаги помогут вам освоить формулу и раскрыть все секреты равнобедренной трапеции!
Структура равнобедренной трапеции и основные параметры
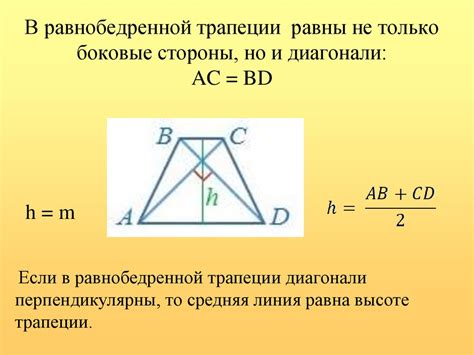
Основные параметры равнобедренной трапеции включают в себя длину параллельных сторон – оснований (a и b), высоту (h), длину бокового ребра (c) и длину диагонали (d). Основания трапеции являются параллельными линиями, которые образуют ее верхнюю и нижнюю границы, а высота – это расстояние между этими основаниями, измеряемое по прямой линии, опущенной из вершины трапеции.
Важно отметить, что высота равнобедренной трапеции является одним из основных параметров и используется при вычислении площади фигуры, а также при решении задач на нахождение других значений, связанных с трапецией.
Знание структуры и основных параметров равнобедренной трапеции позволяет легче разбираться в задачах, связанных с данной геометрической фигурой, и выполнять ее расчеты более точно и эффективно.
Значимость высоты в процессе определения параметров равнобедренной трапеции

Анализ высоты позволяет определить уровень симметрии трапеции, то есть степень равенства длин боковых сторон и прилегающих углов фигуры. Чем ближе значения этих параметров к равенству, тем более симметричной будет трапеция.
Также высота позволяет определить площадь трапеции. Этот параметр оказывается важным в различных практических задачах, таких как расчет площади поверхности фигуры или объема пространства внутри нее.
Шаг 1: Определение длин оснований трапеции
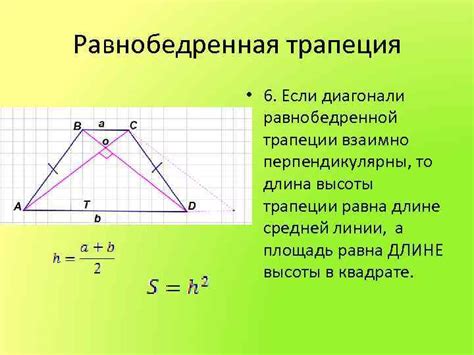
Перед началом расчета высоты равнобедренной трапеции необходимо определить длины ее оснований. Основания трапеции представляют собой пару параллельных отрезков, которые образуют ее боковые стороны. Для нахождения длин оснований можно использовать различные методы измерения или известные значения.
Один из способов определения длин оснований - использование измерительной ленты или линейки. Проведите ленту или линейку вдоль верхней и нижней сторон трапеции и убедитесь, что они параллельны. Следует точно измерить длины этих сторон и записать полученные значения в единицах измерения, таких как сантиметры или дюймы.
| Основание | Длина (в единицах измерения) |
|---|---|
| Верхнее основание | Введите значение |
| Нижнее основание | Введите значение |
Если вы знаете значения диагоналей трапеции и угла между ними, то можно применить теорему косинусов для определения длин оснований. Данная теорема связывает длины сторон треугольника и косинус угла между ними и может быть использована для вычисления относительно простых и треугольных форм.
Вычисление длин оснований является первым важным шагом для определения высоты равнобедренной трапеции и позволяет перейти к следующим этапам расчета.
Шаг 2: Определение длины второстепенной стороны
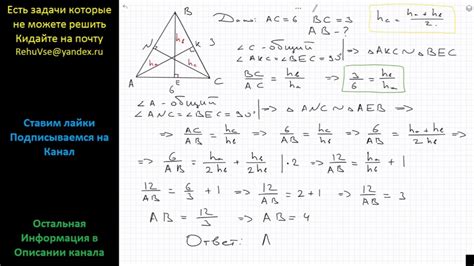
Для вычисления длины боковой стороны необходимо знать значение угла между основанием и этой стороной. Этот угол может быть указан в градусах или радианах. При использовании градусов, можно воспользоваться тригонометрическими функциями, такими как синус или косинус, чтобы найти длину боковой стороны.
Если вам известен угол в радианах, можно использовать его для вычисления длины боковой стороны, используя соответствующие значения тригонометрических функций. Например, синус угла и радиус окружности, описанной вокруг трапеции, помогут определить величину боковой стороны.
Также есть специальные формулы, которые позволяют вычислить длину боковой стороны на основе длин оснований и угла между ними. Например, если границы трапеции продлить до пересечения, мы получим два треугольника, в которых можно использовать теорему синусов для определения длин боковых сторон.
Используя эти простые шаги, можно легко определить длину боковой стороны равнобедренной трапеции. Это позволит нам продолжить расчеты и найти высоту фигуры, что является важным этапом в практических приложениях и задачах по геометрии.
Шаг 3: Применение алгоритма для определения высоты треугольника
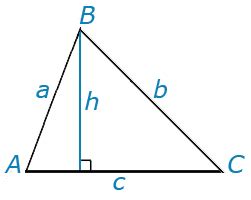
Теперь, когда мы понимаем общую концепцию расчета высоты равнобедренной трапеции, настало время применить соответствующий алгоритм для определения этого значения. Давайте рассмотрим процесс более подробно.
Для начала, нужно определить основание треугольника – это сегмент, на котором треугольник опирается. Затем, следует найти длину бокового ребра треугольника – это отрезок, который соединяет вершину треугольника с основанием. Кроме того, мы должны учесть, что треугольник является равнобедренным, то есть его боковые ребра имеют одинаковую длину.
Имея все необходимые значения – длину основания и длину одного из боковых ребер, мы можем применить формулу для расчета высоты треугольника. Эта формула поможет нам определить вертикальное расстояние от основания до вершины треугольника.
Таблица ниже демонстрирует шаги, которые нужно выполнить для применения формулы и получения окончательного значения высоты равнобедренной трапеции.
| Шаг | Описание |
|---|---|
| Шаг 1 | Определите длину основания треугольника |
| Шаг 2 | Определите длину бокового ребра треугольника |
| Шаг 3 | Используйте формулу для расчета высоты треугольника |
| Шаг 4 | Получите окончательное значение высоты треугольника |
Примеры решения задач с использованием принципа определения высоты равнобедренной трапеции
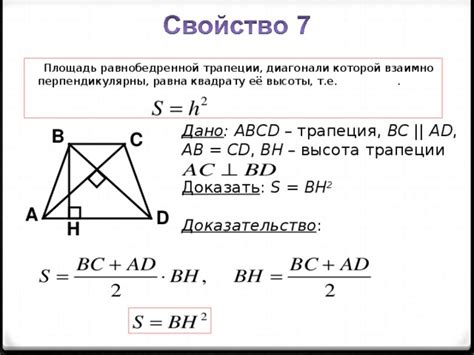
Погрузимся в решение различных задач, активно используя принцип определения высоты равнобедренной трапеции. Разберемся с этим методом на примерах и увидим, как он применяется на практике.
Пример 1:
- В задаче даны две параллельные стороны равнобедренной трапеции и угол между ними. С помощью формулы определения высоты мы вычисляем данное значение.
- Затем, используя данную высоту, мы можем рассчитать другие параметры, такие как площадь или периметр трапеции.
Пример 2:
- В задаче даны площадь и одна из сторон равнобедренной трапеции. Мы можем использовать формулу для рассчета высоты, исходя из данных.
- Это позволяет нам определить вторую сторону трапеции и другие геометрические параметры.
Пример 3:
- В задаче даны периметр и одна из сторон равнобедренной трапеции. С помощью формулы расчета высоты мы находим нужное значение.
- Известные параметры, полученные с использованием формулы, помогают нам решить задачу и найти остальные параметры трапеции.
Эти примеры показывают, что использование формулы определения высоты равнобедренной трапеции является эффективным способом решения задач на практике. С ее помощью мы можем находить различные параметры трапеции и решать разнообразные геометрические задачи.
Вопрос-ответ

Как вычислить высоту равнобедренной трапеции?
Для вычисления высоты равнобедренной трапеции можно использовать формулу, основанную на теореме Пифагора. Высота равнобедренной трапеции равна произведению длины основания и половины разности длин боковых сторон, деленному на длину боковой стороны. Полученное значение можно выразить следующей формулой: h = (a - b) / (2 * c) * c, где a и b - длины оснований, а c - длина боковой стороны.
Какую формулу можно использовать для определения высоты равнобедренной трапеции?
Для определения высоты равнобедренной трапеции можно использовать формулу, основанную на теореме Пифагора. Формула выглядит следующим образом: h = (a^2 - b^2)^0.5, где h - высота, a и b - длины оснований трапеции. Просто вставьте значения длин оснований в формулу и выполните вычисления, чтобы получить значение высоты.
Как вычислить высоту равнобедренной трапеции с помощью формулы?
Для вычисления высоты равнобедренной трапеции можно использовать формулу, основанную на теореме Пифагора. Формула выглядит следующим образом: h = √(a^2 - ((a - b)^2 / 4)), где h - высота, a и b - длины оснований. Вставьте значения длин оснований в формулу и выполните необходимые вычисления (возведение в степень, извлечение квадратного корня и деление), чтобы получить значение высоты равнобедренной трапеции.



