Неотъемлемой частью геометрических построений является умение вписывать окружность внутри треугольника. Такая задача требует от нас точности, аккуратности и навыков работы с инструментами – в данном случае, с циркулем. Многие виды стохастических построений, в которых используется окружность, основываются на этой операции.
Прежде всего, важно иметь перед собой треугольник и циркуль с металлической ножкой. Данная процедура не только позволяет создавать эстетически привлекательные дизайны, но и играет значительную роль в решении различных задач, связанных с геометрией. Вследствие этого, освоение методов вписывания окружности является весьма важным шагом на пути к пониманию более сложных аспектов геометрии и его применения.
В данной пошаговой инструкции мы рассмотрим ключевые шаги для вписывания окружности в треугольник без использования терминов, которые описывают конкретные формы. Наш подход позволит вам овладеть навыками искусства геометрии и развить ваше понимание основных принципов. Что ж, давайте начнем наше путешествие по миру геометрических конструкций!
Введение в основные понятия

Этот раздел позволит вам ознакомиться с фундаментальными терминами, которые будут широко использоваться в данной статье для описания процесса выполнения задачи.
Мы рассмотрим основные понятия, необходимые для понимания процесса вписывания окружности в треугольник с помощью циркуля. Отточите свои знания о геометрии и углубитесь в мир математических конструкций.
Фигура - это всегда предмет интереса в геометрии. Конкретные фигуры могут быть различными - треугольниками, окружностями, прямоугольниками и т.д. В данном контексте, нашим основным фокусом являются треугольники и окружности.
Циркуль - это инструмент, используемый для рисования окружностей и описания дуг. Он состоит из двух ног соединенных суставом, одна из них с ручкой, а другая с острым концом.
Вписанная окружность - это окружность, которая лежит внутри треугольника и касается всех его сторон. Она имеет свойство быть тангентной ко всем сторонам треугольника, а также проходит через его трех биссектрис.
Биссектриса - это прямая, которая делит угол пополам. В треугольнике каждый из трех углов имеет свою биссектрису. Биссектрисы пересекаются в одной точке - центре вписанной окружности.
Глубже изучив эти основные термины, вы будете готовы к выполнению поставленной задачи по вписыванию окружности в треугольник с помощью циркуля. Перейдем к следующему шагу для подробного разбора процесса.
Условия, определяющие вписанность окружности в треугольник
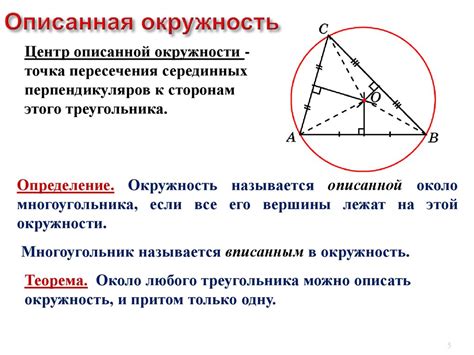
В данном разделе мы рассмотрим основные условия, при которых окружность может быть вписана в треугольник. Эти условия позволяют определить, когда треугольник подходит для вписывания окружности, тем самым образуя важную геометрическую конструкцию.
Первое условие связано с тем, что вписанная окружность касается всех трех сторон треугольника. Без выполнения этого условия окружность не может быть вписана и треугольник не будет соответствовать требованиям. Касание окружности каждой стороны треугольника образует секущие, которые могут быть использованы для анализа вписанности.
Второе условие заключается в том, что точка касания окружности и треугольника должна быть одна и та же для всех трех сторон. Это означает, что окружность должна быть вписана равномерно, не смещаясь в сторону одной из сторон треугольника. В противном случае окружность будет касаться треугольника в разных точках, что не соответствует идее вписанной окружности.
Третье условие связано с углами треугольника. Углы треугольника, которые опираются на точки касания окружности и треугольника, должны быть прямыми. Это значит, что окружность должна быть вписана таким образом, чтобы ее точки касания с треугольником были находились на середине каждой из сторон. Только в этом случае возникают прямые углы и геометрическая конструкция считается вписанной окружностью.
Именно выполнение всех этих условий позволяет получить треугольник, в который возможно вписать окружность. Эти условия определяют валидность и правильность геометрической конструкции и являются основой для дальнейших шагов при использовании циркуля для вписывания окружности в треугольник.
Подготовка к началу построения

В данном разделе рассматривается подготовительный этап перед непосредственным построением фигуры. На этом этапе необходимо выполнить ряд действий, чтобы гарантировать успешное вписывание окружности в треугольник при помощи циркуля.
Первым шагом является выбор подходящего инструмента, который обладает возможностью создавать окружность заданного радиуса. Циркуль является наиболее предпочтительным выбором в данном случае, поскольку он позволяет легко и точно рисовать окружности.
Кроме выбора инструмента, важно также подготовить рабочую поверхность. Для этого необходимо убедиться, что рабочая плоскость чиста от пыли и посторонних предметов, чтобы предотвратить возможные искажения при построении окружности.
Также требуется установить длины сторон треугольника, с которым будет производиться вписывание окружности. Для этого можно использовать линейку или другие инструменты для измерений, в зависимости от доступных возможностей. Корректное определение длин сторон является ключевым этапом в построении окружности.
Построение окружности внутри треугольника с использованием циркуля: последовательность действий
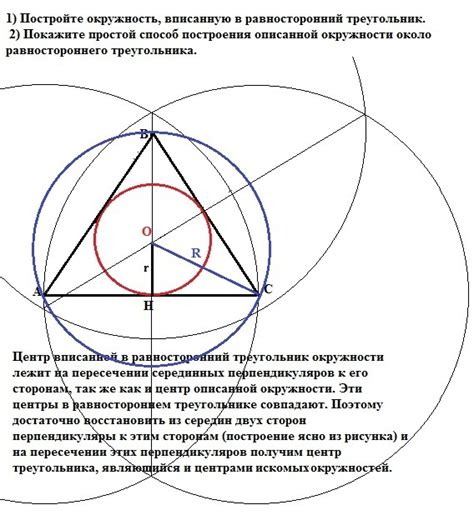
В этом разделе будет представлена подробная инструкция по созданию окружности, которая идеально вписывается в треугольник. Мы описываем пошаговые действия, которые помогут вам достичь желаемого результата.
Перед началом работы убедитесь, что у вас есть циркуль и треугольник. Процесс включает использование различных методов и техник, чтобы создать точное и глубокое впечатление окружности, без использования сложных математических расчетов.
Шаг за шагом, вы будете ознакомлены с детализированной последовательностью действий, включающей определение точек пересечения, создание отрезков и проведение нужных линий. Вы также узнаете, как использовать циркуль для получения нужных радиусов и высоты окружности.
Убедитесь, что вы следуете инструкциям внимательно и точно, чтобы достичь идеального результата. Помимо того, что такая окружность выглядит красиво, она также является важным инструментом в геометрии и может быть полезным для решения различных задач.
Готовы начать построение окружности внутри треугольника? Тогда приступим к деталям!
Прахтическое применение: разносторонний опыт по использованию циркуля в геометрии

Одной из фундаментальных задач геометрии является вписывание окружности в треугольник, и циркуль является неотъемлемым инструментом для достижения этой цели. Здесь мы рассмотрим различные аспекты и приемы, которые помогут вам освоить этот процесс и использовать его в других геометрических задачах.
В этом разделе мы обсудим применение циркуля в процессе построения геометрических фигур и анализа свойств треугольников. Вы узнаете, как использовать циркуль для определения координат центра окружности, проходящей через все вершины треугольника. Также будут рассмотрены различные методы определения радиуса этой окружности, а также способы нахождения точек пересечения окружности с сторонами треугольника.
Раздел также охватывает вопросы практического применения вписывания окружности в треугольник в различных областях, таких как архитектура, дизайн и инженерия. Реальные примеры и задачи помогут вам применить полученные знания на практике и расширить свой навык работы с циркулем.
Под руководством нашей пошаговой инструкции, вы поймете, как использовать циркуль эффективно и с уверенностью, чтобы вписать окружность в треугольник, а также научитесь применять этот метод в других геометрических задачах. Этот раздел поможет вам расширить свои знания и умения в области геометрии и сделает вас более самостоятельными и уверенными в своих достижениях.
Вопрос-ответ

Как определить точку вписывания окружности в треугольник с помощью циркуля?
Чтобы определить точку вписывания окружности в треугольник с помощью циркуля, необходимо найти середину противоположной стороны треугольника. Для этого можно воспользоваться линейкой, проведя прямую через вершину треугольника и середину стороны, либо использовать угольник для определения середины. Эта точка будет центром окружности, вписанной в треугольник.