Вокруг нас окружают разнообразные геометрические фигуры, с каждой из которых связаны определенные законы и численные характеристики. Одной из самых известных и важных фигур является круг, который привлекает внимание своей гладкостью и совершенством своей формы. Возможно, многие из нас задавались вопросом о том, как определить площадь круга по его диаметру и числу, которое мы привыкли называть "пи".
Оказывается, существуют математические формулы, за помощью которых мы можем раскрыть все секреты, связанные с этой удивительной геометрической фигурой. Но прежде чем мы приступим к рассмотрению этих формул, давайте остановимся на ключевых понятиях, которые помогут нам полностью понять суть этого процесса.
Центральная фигура на плоскости, круг подобен взгляду в линзу. Он не только привлекает своей формой и симметрией, но и является важным объектом изучения в математике. Круг может быть определен с помощью нескольких характеристик, включая его радиус и диаметр. Радиус – это расстояние от центра круга до любой его точки, а диаметр является прямым соединением двух точек на краях круга через его центр.
Значимость площади круга и ее роль в геометрии
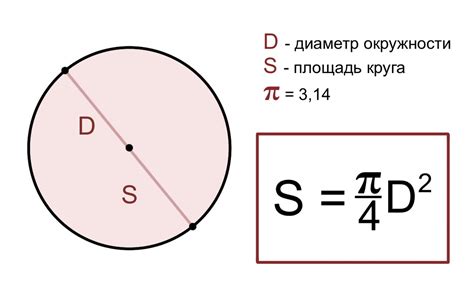
Площадь круга представляет собой количество плоской поверхности, заключенной внутри этой фигуры. Она выражается численным значением и имеет важное значение в различных областях знаний. Например, в математике площадь круга используется при решении задач по геометрии, а также в формулах и уравнениях, связанных с этой фигурой. В физике площадь круга также является важной характеристикой, влияющей на ряд физических закономерностей.
Знание площади круга позволяет определить его вместимость, использовать в формулах для расчета объема и плотности, а также проводить различные аналитические исследования. Многие инженерные решения и строительные проекты требуют учета площади кругов, что позволяет оптимально использовать ресурсы и достичь желаемых результатов.
Важность площади круга | Вразных областях науки и практики, площадь круга играет ключевую роль. |
Значение площади круга | Представляет собой количество плоской поверхности, заключенной внутри круга, и выражается численным значением. |
Применение площади круга | Находит применение в математике, физике, инженерии, архитектуре и других областях, где необходимо исследование и расчеты, связанные с этой геометрической фигурой. |
Определение радиуса круга на основе его диаметра

1. Радиус и диаметр круга
Прежде чем перейти к методам нахождения радиуса, рассмотрим определение радиуса и связанных с ним понятий. Радиус круга - это отрезок соединяющий центр круга с любой точкой его окружности. Диаметр круга - это отрезок, проходящий через центр и соединяющий две точки на окружности.
2. По формуле радиуса и диаметра
Наиболее простым способом нахождения радиуса круга является использование формулы, связывающей радиус и диаметр. Для этого нужно разделить значение диаметра на 2:
Радиус = Диаметр / 2
Например, если известен диаметр круга и он равен 10 единицам, то:
Радиус = 10 / 2 = 5
Таким образом, радиус данного круга равен 5 единицам. Эту формулу можно использовать в любых единицах измерения, будь то сантиметры, метры, футы и т.д.
3. Графический метод
Другим способом нахождения радиуса круга является использование графического метода. Для этого необходимо провести линию, соединяющую центр круга с одной из точек его окружности. Затем измерить длину этой линии и разделить ее на 2. Результат будет радиусом круга.
4. Использование теоремы Пифагора
Теорема Пифагора также может помочь в вычислении радиуса круга. Для этого необходимо знать длину хорды круга - отрезка, соединяющего две точки на окружности. По формуле теоремы Пифагора:
Радиус = √(Диаметр² - Хорда²) / 2
Таким образом, с помощью теоремы Пифагора можно найти радиус круга, имея информацию о длине диаметра и хорды.
В данном разделе мы рассмотрели несколько методов нахождения радиуса круга по его диаметру. В зависимости от известных данных и задачи, можно выбрать наиболее удобный способ для вычисления радиуса и использовать его при необходимости.
Расчет площади круга при известном радиусе
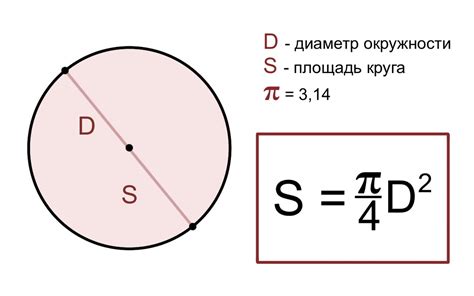
- Шаг 1: Запишите значение радиуса круга. Радиус - это расстояние от центра круга до любой его точки.
- Шаг 2: Используйте формулу площади круга: площадь = π * (радиус в квадрате).
- Шаг 3: Вставьте известное значение радиуса в формулу и вычислите значение его квадрата.
- Шаг 4: Умножьте значение квадрата радиуса на значение математической константы "π". Полученное число и будет площадью круга.
Таким образом, расчет площади круга при известном радиусе является довольно простым и основывается на использовании формулы, которая использует радиус и константу "π". Следуя указанным шагам, вы сможете точно вычислить площадь круга, зная его радиус.
Вычисление площади круга: способ по диаметру
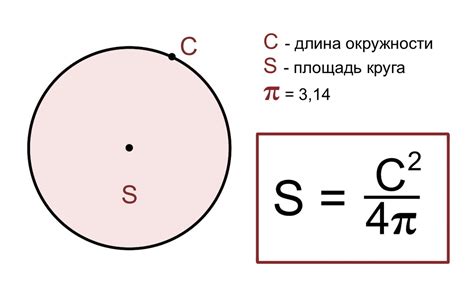
Для вычисления площади круга по диаметру необходимо знать значение числа π и длину диаметра. Число π, оно также известно как пи, является математической константой примерно равной 3,14159.
Чтобы найти площадь круга, можно использовать следующую формулу: площадь = (π * (диаметр / 2)^2).
Определите значение числа π (пи). В качестве приближенного значения можно использовать 3,14 или более точное число, если это необходимо для вашей задачи. Затем измерьте диаметр круга.
Разделите значение диаметра на 2. Это позволит найти радиус, то есть расстояние от центра круга до любой точки на окружности.
Возводите полученное значение радиуса в квадрат и умножайте на значение числа π (пи).
Полученный результат будет являться площадью круга, обозначенную в квадратных единицах, так как площадь всегда измеряется в квадратных единицах.
Используйте указанные шаги и формулу для вычисления площади круга по его диаметру и числу π. Знание этих вычислений поможет вам решать задачи, связанные с определением площади кругов в различных контекстах.
| Шаг | Действие |
|---|---|
| 1 | Определите значение числа π (пи). |
| 2 | Измерьте диаметр круга. |
| 3 | Разделите значение диаметра на 2, чтобы найти радиус. |
| 4 | Возводите значение радиуса в квадрат. |
| 5 | Умножьте значение квадрата радиуса на число π (пи). |
Преимущества числа Пи при вычислении площади круга

Чтобы вычислить площадь круга с использованием числа Пи, мы должны знать его радиус или диаметр. Радиус - это расстояние от центра круга до любой точки на его окружности, и диаметр - это расстояние между двумя точками на окружности, проходящими через центр. Применяя формулу, основанную на числе Пи, мы можем найти площадь круга и получить точный результат.
| Величина | Формула |
|---|---|
| Площадь круга | Пи * (Радиус)^2 |
| Площадь круга | Пи * ((Диаметр/2))^2 |
Например, если у нас есть круг с радиусом 5 единиц, чтобы найти его площадь, мы можем использовать формулу: Пи * (5)^2. Просто подставляя значения в формулу и выполняя вычисления, мы получим точный результат.
Использование числа Пи для вычисления площади круга является надежным и точным методом. Однако, приближенные значения числа Пи могут быть использованы, если требуется грубая оценка площади круга. В таких случаях, может быть использовано значение 3.14 или 22/7 вместо более точного числа Пи.
Примеры расчета площади круга с использованием диаметра и числа π
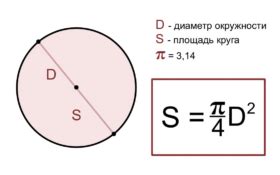
Различные способы расчета площади круга с использованием известного диаметра и значения числа π
Расчет площади круга – важная задача, которая встречается в разных областях науки и практики. Для проведения таких расчетов необходимо знать диаметр круга и значение числа π. Существует несколько способов определения площади круга с использованием этих данных.
Ниже приведены несколько примеров, демонстрирующих различные методы вычисления площади круга на основе известного диаметра и значения числа π:
1. Используя формулу: площадь круга равна половине произведения диаметра на π.
2. Путем возведения в квадрат радиуса круга (равного половине диаметра) и умножения результата на π.
3. Используя соотношение между длиной окружности и площадью круга, где длина окружности равна произведению диаметра на π, а площадь круга равна четверти квадрата диаметра, умноженного на π.
Зная эти методы, можно точно рассчитать площадь круга на основе его диаметра и значения числа π. Эти примеры способствуют более полному пониманию процесса расчета площади круга и повышают уровень математической грамотности.
Вопрос-ответ

Как вычислить площадь круга по диаметру и числу пи?
Для вычисления площади круга по диаметру и числу пи необходимо умножить квадрат диаметра на число пи и поделить полученный результат на 4. Формула выглядит следующим образом: S = (pi * d^2) / 4, где S - площадь круга, d - диаметр круга. Например, если диаметр круга равен 10 см, то площадь можно вычислить следующим образом: S = (3.14 * 10^2) / 4 = 78.5 см^2.
Какие значения использовать для числа пи при вычислении площади круга?
Обычно при вычислении площади круга используют значение числа пи, округленное до двух знаков после запятой: 3.14. Это приближенное значение числа пи достаточно точно для большинства применений. Однако, если требуется большая точность, то можно использовать более длинную десятичную запись числа пи – 3.14159 или воспользоваться специальными математическими библиотеками, которые хранят число пи с большей точностью.
Какие единицы измерения использовать для диаметра при вычислении площади круга?
При вычислении площади круга по диаметру можно использовать любые единицы измерения, например сантиметры (см), метры (м), дюймы (инчи) и т.д. Главное, чтобы значения диаметра и площади были в одинаковых единицах измерения. Например, если диаметр указан в сантиметрах, то площадь будет выражена в квадратных сантиметрах (см^2).