Представьте себе, что вы входите в огромный зал, наполненный загадочными фигурами и символами. Вокруг вас только таинственное молчание и увлекательные задачи, которые требуют вашей сообразительности и математического мышления. Среди них - задача о нахождении периметра круга с диаметром. Этот загадочный процесс расчета окружности покоряет умы ученых уже веками, и сегодня предлагаем вам погрузиться в мир специализированных методов, которые сделают эту задачу легкой и эффективной.
Диаметр окружности - это нечто уникальное, подобно стержню, связывающему две противоположные точки ее края. Огромное количество проблем в нашей жизни сводится к поиску и определению этой загадочной величины. Но вот представьте: у вас есть диаметр окружности, и вы хотите посчитать периметр - то есть длину всей окружности. Как кажется на первый взгляд, достаточно знать диаметр, и можно сделать простую операцию - умножить его на число "pi" (π). И тут возникает очевидный вопрос: каким образом получается это знаменитое число π? И что делать, если мы не знаем его точного значения, а задача требует найти периметр?
Стандартный алгоритм нахождения периметра круга может показаться скучным и однообразным, но в то же время он основан на фундаментальных принципах геометрии и математики. Однако существуют и более эффективные методы расчета, которые позволяют найти периметр круга даже без знания точного значения числа π. Давайте вместе отправимся в путешествие по миру геометрии, чтобы узнать о некоторых удивительных и интуитивно понятных подходах, которые помогут нам разгадать эту задачу и сделать наш расчет максимально эффективным.
Основные принципы и формулы для вычисления периметра окружности
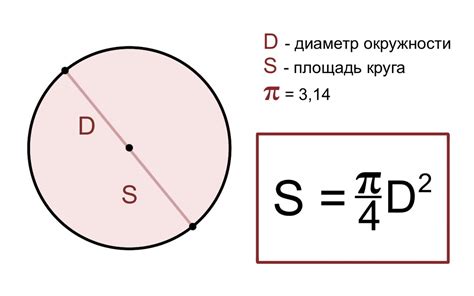
Периметр окружности - это длина замкнутой линии, ограничивающей плоскую фигуру, для которой характерно равноудаление всех точек на плоскости от определенной точки - центра окружности.
Для вычисления периметра окружности существует несколько формул, которые базируются на различных характеристиках данной фигуры. Наиболее распространенной из них является формула, связывающая периметр с диаметром окружности. Умение применять данную формулу позволяет эффективно и быстро решать задачи связанные с нахождением периметра окружности.
- Диаметр окружности - это прямая линия, проходящая через центр и две противоположные точки на окружности. Величина диаметра можно найти, зная радиус окружности или наоборот.
- Радиус окружности - это расстояние от центра окружности до любой точки на ее границе.
- Формула для вычисления периметра окружности через диаметр: \(P = \pi \cdot d\) (где \(P\) - периметр, \(\pi\) - математическая константа, примерно равная 3,14, \(d\) - диаметр).
- В случае, если известен радиус окружности, а не диаметр, формула будет выглядеть следующим образом: \(P = 2\pi \cdot r\) (где \(P\) - периметр, \(\pi\) - математическая константа, примерно равная 3,14, \(r\) - радиус).
Используя указанные формулы, вы сможете рассчитывать периметр окружности с помощью диаметра или радиуса. Это даст вам возможность эффективно проводить расчеты и применять их в решении различных практических задач.
Связь между диаметром, радиусом и длиной окружности круга
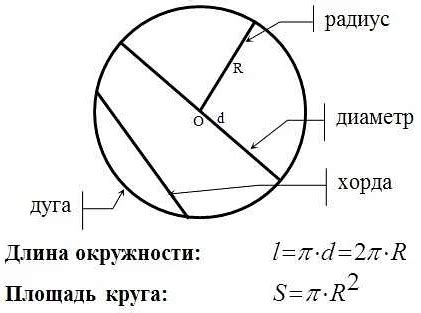
Когда речь заходит о периметре круга с заданным диаметром, важно понимать, что есть особая связь между диаметром и другими характеристиками круга, такими как радиус и длина окружности. Эти величины взаимосвязаны и позволяют производить расчеты периметра круга исходя из разных известных значений.
При обсуждении периметра круга необходимо учитывать, что диаметр - это отрезок, соединяющий две точки на окружности круга и проходящий через его центр. Более того, диаметр можно использовать для вычисления радиуса круга. Являясь половиной диаметра, радиус представляет собой расстояние от центра круга до любой точки его окружности. Эта связь между диаметром и радиусом позволяет нам легко переходить от одной из этих величин к другой при расчетах периметра.
Другой важной характеристикой круга, связанной с его периметром, является длина окружности. Длина окружности - это расстояние между точками на окружности круга, измеряемое вдоль его контура. Стоит отметить, что длина окружности тесно связана с диаметром круга. В частности, длина окружности можно выразить как произведение диаметра на число π (пи). Используя эту связь, мы можем проводить расчеты периметра круга на основе известной длины окружности и наоборот.
Рассчитываем длину окружности с помощью диаметра
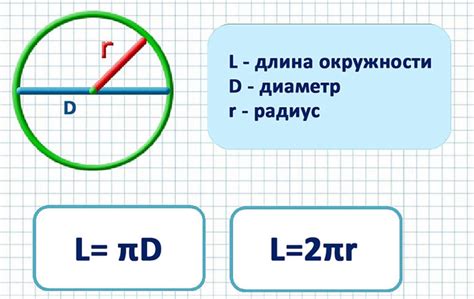
Длина окружности – это периметр фигуры, образуемый ее границей. В случае окружности, нахождение длины окружности связано с использованием диаметра – отрезка, проходящего через центр и ограничивающий ее фигуру.
Зная диаметр окружности, можно рассчитать ее длину с высокой точностью. Важно отметить, что длина окружности пропорциональна ее диаметру и имеет фиксированное отношение к нему. Это отношение известно как ∡ (примерно равно 3.14) или пи-число.
Таким образом, чтобы рассчитать длину окружности, необходимо умножить диаметр на значение пи. Формула для расчета:
Длина окружности = Диаметр × Пи
Применение этой формулы позволяет быстро и точно определить длину окружности, что может быть полезно при проектировании, строительстве, геодезии и других областях науки и техники, где требуется работа с окружностями.
Способы определения обвода круга при известном диаметре и радиусе

Первый метод
Один из способов вычисления периметра круга основан на знании его диаметра. Используя формулу для вычисления длины окружности, которая основана на диаметре, мы можем легко найти обвод круга. Формула имеет простую структуру и может быть применена без особых сложностей.
Примерно так же, как диаметр делится пополам для определения радиуса, формула также учитывает эту зависимость. Зная диаметр, мы можем использовать его удвоенное значение для расчета обвода круга.
Второй метод
Другой способ определения периметра круга основан на его радиусе. Радиус – это половина диаметра, и мы можем использовать эту информацию для нахождения обвода. Формула для вычисления обвода круга на основе радиуса достаточно проста и требует вычисления произведения радиуса на удвоенное значение числа «пи».
Такой подход предлагает использовать радиус вместо диаметра в формуле окружности. Это достаточно удобно, особенно когда в расчетах могут присутствовать другие параметры, зависящие от радиуса.
В итоге, в данном разделе мы рассмотрели два различных метода определения периметра круга по известному диаметру и радиусу. Оба метода являются простыми и эффективными, позволяя легко получить значение периметра и использовать его в дальнейших вычислениях или задачах геометрии.
Примеры определения длины окружности, основанные на длине диаметра
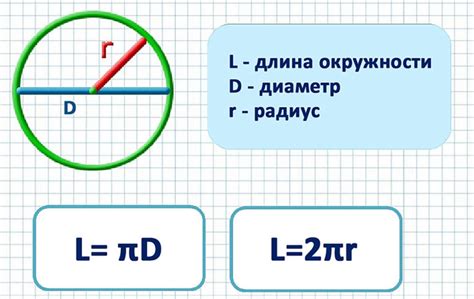
1. Пример 1: Определение длины окружности с помощью формулы
Если известна длина диаметра круга, то длину окружности можно рассчитать по простой формуле, используя значения радиуса (половину диаметра) и числа "π". Например, пусть длина диаметра круга равна 10 сантиметрам. Для определения длины окружности следует умножить значение радиуса (5 сантиметров) на два и затем умножить такое значение на число "π" (приближенное значение: 3.14159). Таким образом, длина окружности равна примерно 31.4159 сантиметра.
2. Пример 2: Определение длины окружности путем измерений
Если диаметр круга доступен для физического измерения, то длину окружности можно определить, используя простую формулу. С помощью измерительной ленты или штангенциркуля, измерьте длину диаметра круга. Затем умножьте полученное значение на число "π", чтобы найти длину окружности. Например, если длина диаметра равна 20 сантиметрам, то длина окружности будет примерно равна 62.83185 сантиметра.
Приведенные примеры демонстрируют различные способы расчета длины окружности на основе длины диаметра. Выбор метода зависит от доступных данных и задачи, которую требуется решить. Определение длины окружности является важным элементом геометрии, широко применяемым в разных областях науки и практики.
Практическое применение расчета окружности в повседневной жизни

Применение расчетов периметра окружности можно найти в архитектуре и строительстве. Например, при проектировании круглых зданий или строительстве колонн, знание периметра круга позволяет точно определить количество материалов, необходимых для возведения объектов такой формы.
Другой пример практического использования расчета периметра окружности связан с инженерными задачами. Знание длины окружности позволяет правильно разместить кабели или трубы нужной длины в технических системах, таких как электроснабжение или водоснабжение.
Также, расчет окружности может быть полезен в области географии и навигации. Знание периметра окружности Земли позволяет определить расстояние между двумя точками на поверхности планеты и использовать это знание для путешествий или маршрутизации.
- Архитектура и строительство
- Инженерия
- География и навигация
В приведенных примерах всего лишь пара областей, где знание методов расчета периметра окружности может быть практически полезным. В целом, понимание этих методов расширяет область применения математических знаний в повседневной жизни и помогает решать разнообразные задачи с учетом геометрических форм.
Альтернативные подходы к определению окружности с заданным диаметром
В данном разделе рассмотрим несколько принципиально различающихся методов определения периметра окружности с заданным диаметром. Вместо использования стандартных алгоритмов, мы предлагаем альтернативные подходы, которые могут быть эффективными в определенных ситуациях.
1. Определение периметра через радиус
Вместо рассмотрения диаметра окружности, мы фокусируемся на радиусе. Мы предлагаем использовать формулу, основанную на радиусе, для определения периметра круга. Этот подход может быть полезен в случаях, когда данные о диаметре неизвестны, но есть информация о радиусе. Такой метод позволяет упростить процесс расчета и получить точный результат.
2. Использование теоремы Пифагора
Мы представляем альтернативный способ нахождения периметра окружности с заданным диаметром при помощи теоремы Пифагора. В этом методе мы соединяем прямоугольные треугольники, образованные диаметром и радиусом, и используем теорему Пифагора для определения полупериметра. Это позволяет получить более точные результаты в сравнении с другими методами и упрощает расчеты.
3. Комплексный подход с использованием рациональных чисел
В этом подходе мы предлагаем использовать комплексные числа и рациональные числа вместо стандартных алгоритмов расчета периметра окружности с диаметром. Комплексные числа обладают уникальными свойствами, которые позволяют более точно вычислять периметр окружности с заданным диаметром. При использовании рациональных чисел, полученный результат может быть представлен точно и без округления.
Эти альтернативные способы определения периметра окружности с заданным диаметром могут быть интересными альтернативами стандартным методам. Их использование может обеспечить более точные и эффективные результаты в зависимости от конкретного случая и требований.
Вопрос-ответ

Как найти периметр круга с диаметром?
Для расчета периметра круга с заданным диаметром необходимо воспользоваться формулой: P = π * d, где P - периметр, π (пи) - математическая постоянная, равная примерно 3,14, а d - диаметр круга.
Какие эффективные методы существуют для расчета периметра круга?
Одним из самых эффективных методов расчета периметра круга является использование формулы P = π * d. Также можно воспользоваться формулой P = 2 * π * r, где r - радиус круга, который можно получить, разделив диаметр на 2.
Как посчитать периметр круга без использования формулы?
Если вы не желаете использовать формулу для расчета периметра круга, можно воспользоваться следующим методом: измерьте диаметр круга с помощью линейки или мерной ленты и умножьте его на значение числа π, которое можно принять как 3,14.
Что делать, если неизвестен диаметр круга?
Если диаметр круга неизвестен, но известен радиус, можно воспользоваться формулой P = 2 * π * r, где P - периметр круга, π - математическая постоянная, равная примерно 3,14, а r - радиус круга. Если известна только площадь круга, можно воспользоваться формулой P = 2 * π * √(S/π), где S - площадь круга.
Какие еще методы расчета периметра круга можно использовать?
Помимо расчета периметра круга с помощью формулы P = π * d или P = 2 * π * r, можно воспользоваться геометрическим методом. Постройте окружность с заданным диаметром на графическом материале и измерьте длину полученного окружности с помощью линейки или мерной ленты.
Как найти периметр круга, если известен его диаметр?
Чтобы найти периметр круга, используется формула: P = π * d, где P - периметр, а d - диаметр. Значение числа π примерно равно 3.14. Поэтому, если вам известен диаметр круга, вы можете найти его периметр, умножив значение диаметра на число π.



