В процессе изучения геометрии часто возникает необходимость определить положение центра фигуры при известном параметре, таком как диаметр. При этом у нас есть возможность использовать специальные методы и формулы, которые позволяют найти координаты центра фигуры без прямого измерения или определения его геометрическими методами.
Установление положения оси при заданном диаметре особенно важно при работе с кругами и множеством других геометрических фигур. Зная, что диаметр - это отрезок, проходящий через центр фигуры и имеющий концы на ее границе, мы можем воспользоваться геометрическими принципами для определения положения осевого средства.
В данной статье мы рассмотрим несколько методов, позволяющих определить координаты центра фигуры на основе известного диаметра. Методы включают в себя аналитический подход с использованием формул, основанных на свойствах геометрических фигур, а также альтернативные методы, использующие измерительные инструменты и специализированное программное обеспечение.
Определение положения центра окружности при известном размере ее диаметра
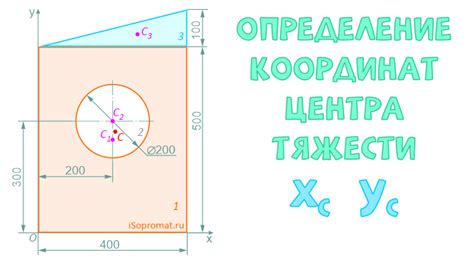
В данном разделе мы рассмотрим методы и подходы к определению положения центра окружности, основываясь на известном значении диаметра. Это важная задача в геометрии, которая находит свое применение в различных областях науки и техники.
Для начала, необходимо уяснить, что центр окружности является математической точкой, которая находится на равном удалении от всех точек окружности. Определение этой точки имеет принципиальное значение, так как она задает геометрическое положение окружности и позволяет установить ее расположение относительно других объектов или плоскостей.
| Метод | Описание |
|---|---|
| Геометрический метод | Основан на проведении перпендикулярных линий к касательной окружности и их пересечении. Этот метод позволяет найти точку пересечения перпендикуляров и определить центр окружности. |
| Аналитический метод | Основан на использовании координатных плоскостей и алгебраических вычислений. Путем решения системы уравнений, состоящей из уравнений окружности и уравнений прямых, можно найти координаты центра окружности. |
| Использование геометрических фигур | Такие фигуры, как треугольники, равнобедренные трапеции или пятиугольники, могут использоваться для определения центра окружности. Отношения и длины отрезков внутри этих фигур могут предоставить информацию о координатах центра окружности. |
В зависимости от конкретной задачи и доступных условий, различные методы могут оказаться более удобными или эффективными. Однако важно помнить о необходимости точности в измерениях и вычислениях, чтобы получить достоверный результат. Каждый из методов имеет свои особенности и требует определенных навыков в геометрии или математике.
Основные понятия в изучении кругов
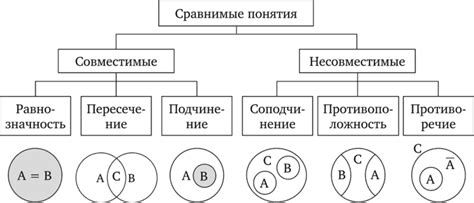
Введение в тему кругов поможет познакомиться с неотъемлемыми понятиями, которые будут использоваться в дальнейшем изучении и понимании работы с кругами. Эти основные термины позволят нам изучить свойства и характеристики круга, а также справиться с задачами, связанными с определением его параметров.
Применение геометрических методов для определения положения центра круга
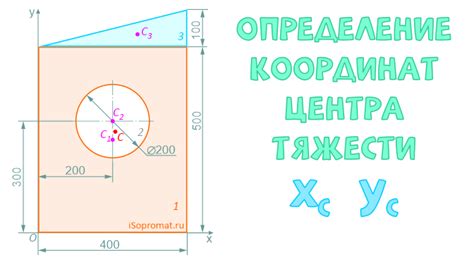
В данном разделе рассматривается использование геометрических методов для определения положения центра круга, основываясь на известном значения диаметра. Знание работы с геометрическими принципами и формулами позволяет точно вычислить координаты центра круга, необходимые для его позиционирования и решения разнообразных задач.
Определение центра круга является важным шагом при работе с геометрическими объектами и создании различных дизайнов. Методы, основанные на использовании геометрических формул и принципов, позволяют с легкостью определить точное положение центра круга и решить сложные задачи, в которых необходимо знание точного положения этого элемента.
Одним из способов определения центра круга является использование координатных плоскостей и формул нахождения координат точки по известным параметрам. Например, с помощью формулы для нахождения середины отрезка можно найти координаты центра окружности по известным координатам двух точек, лежащих на диаметре.
Другим методом является использование теоремы о перпендикулярах и серединах отрезков. Зная координаты двух точек на диаметре круга и применяя данную теорему, можно определить координаты центра при помощи формул вычисления середины отрезка и нахождения перпендикуляра.
Использование геометрических методов для определения положения центра круга при известном диаметре способствует точному и эффективному решению задач, связанных с работой с геометрическими объектами. Корректное определение положения центра круга является важным аспектом в создании дизайнов, строительстве, машинной графике и других областях, где требуется работа с окружностями и кругами.
Применение системы координат для определения положения центра окружности с известным диаметром
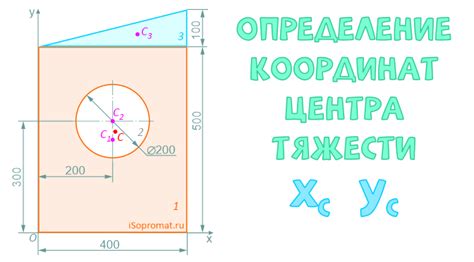
Система координат состоит из двух перпендикулярных осей - горизонтальной (ось x) и вертикальной (ось y). Их пересечение обозначает начало координат, обычно обозначаемое буквами O или (0,0).
Когда мы имеем информацию о диаметре окружности, мы можем использовать систему координат для определения координат центра окружности. Поскольку диаметр проходит через центр окружности, мы можем найти две точки на окружности, через которые проходит диаметр. Зная координаты этих двух точек, мы можем найти середину отрезка между ними, что будет точкой центра окружности.
Пользуясь системой координат, мы можем легко определить положение центра окружности в пространстве. Это особенно полезно при работе с геометрическими задачами и визуализации объектов, таких как окружности с известным диаметром.
Вычисление среднего арифметического координат

Для определения центра круга при известном диаметре нам необходимо подсчитать среднее арифметическое значение координат всех точек, лежащих на границе данного круга. Этот метод позволяет нам точно определить положение центра круга на плоскости.
Для начала, нам необходимо получить координаты каждой точки на границе круга. Для этого можно использовать различные способы, например, вычислить координаты точек на окружности, используя формулы тригонометрии или выполнив нужные геометрические конструкции.
После получения всех координат, необходимо сложить все значения для каждой из осей координат и разделить их на общее количество точек. Таким образом, мы получим среднее значение по X и по Y координатам.
Итак, чтобы определить центр круга при известном диаметре, мы вычисляем среднее арифметическое значение координат всех точек на границе круга. Этот подход позволяет нам точно определить положение центра круга на плоскости и использовать эту информацию для различных геометрических задач.
Узнавание центра окружности при помощи циркуля и линейки
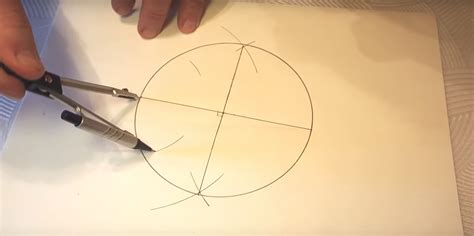
В этом разделе мы рассмотрим метод, который позволяет определить центр окружности, не зная его точного положения и диаметра. Благодаря использованию обычной линейки и циркуля, мы сможем установить центр окружности с достаточной точностью, позволяющей дальнейшую работу с данным геометрическим объектом.
Основная идея метода заключается в построении перпендикуляров к хорде окружности, а затем в поиске их точки пересечения. Это сделать легко и просто с помощью циркуля и линейки, используя простые геометрические конструкции. Этот метод является универсальным и может применяться на практике для нахождения целого ряда центров окружностей различных размеров и форм.
В следующих разделах мы более подробно рассмотрим каждый шаг метода и дадим конкретные инструкции по его выполнению. Мастерство использования циркуля и линейки, а также понимание геометрических конструкций позволят вам уверенно определять центр окружности, даже в тех случаях, когда ни размеры, ни форма окружности вам неизвестны.
Области применения полученных знаний

Получение знаний о центре круга при известном диаметре предоставляет возможности для применения в различных областях, где использование геометрии и расчетов имеет существенное значение.
Одной из областей, где данное знание может быть полезным, является архитектура и строительство. Знание о центре круга при известном диаметре позволяет строителям и архитекторам правильно размещать и располагать элементы построек, такие как колонны, арки, купола и другие конструктивные элементы. Точное определение центра круга поможет обеспечить стабильность и прочность сооружений.
В инженерии и машиностроении знание о центре круга при известном диаметре может быть полезным при разработке и конструировании различных механизмов и деталей. Такие знания позволяют точно располагать отверстия, оси вращения и другие ключевые элементы, обеспечивая правильное функционирование и соответствие требованиям проекта.
В области геодезии и картографии знание о центре круга при известном диаметре может быть полезным при создании карт и определении координат точек на земной поверхности. Это позволяет осуществлять точные измерения и определение местоположения объектов, что является важным в таких областях, как навигация, планирование транспортных маршрутов и геологические исследования.
Практические упражнения и примеры: поиск середины окружности

Этот раздел предлагает набор практических упражнений и примеров, которые помогут вам научиться находить середину окружности при заданном диаметре. Здесь вы найдете пошаговые инструкции и конкретные примеры для разных ситуаций.
- Упражнение 1: Определение середины окружности с помощью компаса и линейки.
- Упражнение 2: Вычисление координат середины окружности по формуле.
- Упражнение 3: Нахождение середины окружности с помощью графического редактора.
В этом упражнении вы научитесь определять середину окружности с использованием простых инструментов, таких как компас и линейка. Шаг за шагом будет показан процесс измерения и построения линии, которая проходит через середину окружности.
В этом упражнении вы узнаете, как вычислить координаты середины окружности, используя формулу. Будут представлены примеры с разными значениями диаметра и известными координатами точек на окружности.
В этом упражнении вы попробуете использовать графический редактор для определения середины окружности. Будут показаны шаги по созданию окружности и нахождению ее середины с помощью инструментов редактора.
Эти практические упражнения и примеры помогут вам развить навыки определения середины окружности при известном диаметре. Вы сможете применить эти знания в различных ситуациях, связанных с геометрией и инженерными расчетами.
Вопрос-ответ

Как определить центр круга при известном диаметре?
Для определения центра круга при известном диаметре необходимо провести две перпендикулярные линии через середину диаметра. Точка пересечения этих линий будет являться центром круга.
Как найти центр круга, если известны только координаты нескольких точек на его окружности?
Если известны координаты нескольких точек на окружности круга, можно провести перпендикулярные биссектрисы для каждой пары точек. Точка пересечения этих биссектрис будет являться центром круга.
Можно ли определить центр круга при известном радиусе, а не диаметре?
Да, можно определить центр круга при известном радиусе. Для этого необходимо провести перпендикуляр к радиусу в его конечной точке. Точка пересечения перпендикуляра и радиуса будет центром круга.
Как определить центр круга на плоскости без использования линейных инструментов?
Если линейные инструменты не доступны, можно взять любые предметы, которые можно использовать в качестве отрезков или шаблонов. Необходимо провести два перпендикулярных отрезка или шаблона через середину диаметра и найти точку пересечения - это будет центр круга.
Что делать, если известна только длина дуги круга? Можно ли определить центр круга?
Если известна только длина дуги круга, нельзя однозначно определить центр круга. Необходимо дополнительно знать хотя бы одну из следующих величин: длину диаметра, радиуса или координаты точек на окружности.