Что же стоит у основы тайной проверки принадлежности точки треугольнику? Ответить на этот вопрос – значит вступить в мир геометрии, где числа, линии и фигуры оживают, раскрывая свои родословные и открывая необычные законы природы.
Мы погрузимся в пространство бесконечных возможностей, где самые простые принципы могут исчезнуть, уступив место магическим операциям и захватывающим трансформациям. Здесь мы наблюдаем неизведанные связи и невероятные открытия, связанные с проверкой принадлежности точки треугольнику.
Оставьте логику позади и взгляните на геометрию в другом измерении, где навыки и тончайшие теоремы приводят нас в мир алгоритмов и методов. Откройте глаза на стирание границ и объединение пространств, где сияют научные доказательства и гениальные идеи.
Следуйте за нами через лабиринты формул и символов, чтобы раскрыть тайну проверки принадлежности точки треугольнику. Вам предстоит стать свидетелем современных революций в мире математики и взглянуть на удивительные практические приложения, способные изменить неподвижный ход вещей. Начните свое путешествие и погрузитесь в глубины этого захватывающего раздела!
Актуальность и задачи исследования

В данном разделе исследуется вопрос о том, как определить, принадлежит ли заданная точка треугольнику. Эта проблема имеет важное практическое значение, например, при работе с графикой, обработке изображений, геоинформационных системах и в других областях, где необходимо определить, входит ли точка внутрь заданной фигуры.
Целью исследования является разработка эффективных алгоритмов и методов проверки принадлежности точки треугольнику, которые позволят выполнять данную задачу с высокой точностью и минимальными вычислительными затратами. Для достижения этой цели необходимо решить следующие задачи:
- Анализ существующих методов проверки принадлежности точки треугольнику и выявление их недостатков.
- Разработка новых алгоритмов, основанных на математических и геометрических принципах, которые позволят эффективно решать указанную задачу.
- Использование современных вычислительных методов и подходов для улучшения производительности предложенных алгоритмов.
- Проверка разработанных методов и алгоритмов на реальных данных и анализ их эффективности по сравнению с другими подходами.
Решение данных задач позволит повысить эффективность и точность процесса проверки принадлежности точки треугольнику, что в свою очередь способствует развитию различных приложений и систем.
Использование барицентрических координат для определения положения точки относительно треугольника
Основная идея метода заключается в том, что каждой вершине треугольника соответствует коэффициент, который показывает вклад этой вершины в представление точки. Сумма всех коэффициентов равна единице. Используя эти коэффициенты, можно определить положение точки относительно треугольника - внутри треугольника, на его границе или за его пределами.
Метод барицентрических координат позволяет проводить ряд операций, таких как вычисление площади треугольника, поиск барицентра треугольника и проверка взаимного расположения двух треугольников. Также данный метод обладает высокой эффективностью и простотой реализации.
- Координаты точки суммируются с весами вершин треугольника
- Сумма весов точки равна единице
- Положение точки определяется в зависимости от значений весов: внутри треугольника, на границе или за пределами
- Метод барицентрических координат обладает высокой эффективностью и простотой реализации
Описание выбранного подхода и его особенности

В данном разделе будет представлен метод, который позволяет определить принадлежность заданной точки к заданному треугольнику. Этот подход отличается своей высокой эффективностью и точностью, а также обладает рядом уникальных особенностей.
Основанная на формуле ориентированной площади проверка принадлежности точки треугольнику
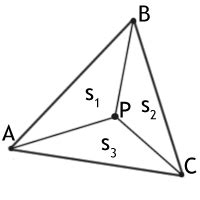
Данная проверка основывается на вычислении ориентированной площади, которая представляет собой числовую характеристику треугольника и зависит от расположения его вершин и заданной точки. Формула ориентированной площади позволяет определить, лежит ли точка слева или справа от стороны треугольника.
При использовании метода на основе формулы ориентированной площади необходимо представить треугольник и точку в виде двумерных координат. Затем, с помощью формулы, вычислить ориентированную площадь треугольника, образованного этими точками. Знак результата определит положение точки относительно треугольника.
Для удобства вычисления ориентированной площади можно воспользоваться различными алгоритмами, такими как алгоритм вычисления детерминанта или алгоритм Грэхэма. Они позволяют с высокой точностью определить положение точки относительно треугольника.
Использование формулы ориентированной площади для проверки принадлежности точки треугольнику является эффективным методом, который находит широкое применение в различных областях, таких как компьютерная графика, геометрия, компьютерное моделирование и другие.
Принцип работы метода и его достоинства
В данном разделе мы рассмотрим принцип работы выбранного метода проверки принадлежности точки треугольнику и обсудим его преимущества.
Перед нами стоит задача определения принадлежности точки некоторому треугольнику. Для решения этой задачи используется разработанный метод, основанный на анализе геометрических характеристик треугольника и его отношения к искомой точке.
Основной принцип работы метода заключается в определении положения точки относительно сторон треугольника и их расстояния до этой точки. Путем сравнения полученных данных и проверки соответствующих условий мы можем однозначно определить, принадлежит ли точка треугольнику или нет.
Главным достоинством данного метода является его эффективность. Это связано с тем, что мы избегаем излишних вычислений и проверок, фокусируясь только на геометрических характеристиках треугольника и относительном положении точки относительно его сторон. Такой подход позволяет существенно сократить время выполнения проверки и сделать ее более оптимальной.
Более того, выбранный метод имеет простую реализацию и не требует большого количества ресурсов, что делает его удобным и доступным для применения в различных областях.
Алгоритм граничных прямых
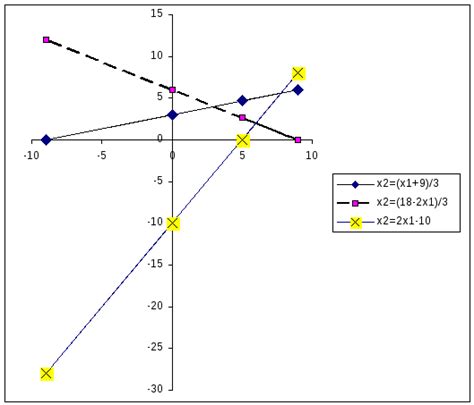
Раздел "Алгоритм граничных прямых" представляет подробное описание метода, который позволяет эффективно и точно определить принадлежность заданной точки к треугольнику. В данном разделе рассмотрены основные принципы работы алгоритма и его достоинства в сравнении с другими методами проверки принадлежности. Особое внимание уделено граничным прямым, которые играют ключевую роль в данном алгоритме.
Статья предоставляет подробный анализ алгоритма граничных прямых, описывающий каким образом могут быть определены такие прямые для заданного треугольника. Данное объяснение включает понятные и наглядные примеры, чтобы помочь читателю лучше понять и освоить данный метод.
Основные преимущества алгоритма граничных прямых, такие как высокая эффективность и точность, подробно обсуждаются в данном разделе. Кроме того, представлены результаты сравнительного анализа алгоритма с другими известными методами проверки принадлежности, что помогает оценить его практическую применимость и превосходство в конкретных сценариях.
Описание алгоритма граничных прямых в данном разделе подкреплено реальными примерами и практическими рекомендациями, позволяющими разбираться с основными трудностями и недостатками данного метода. Также освещены возможные области его применения и дальнейшие направления исследований, которые могут улучшить его эффективность и расширить его функциональные возможности.
Использование алгоритма и оценка его эффективности
В данном разделе описывается подробное рассмотрение алгоритма, который позволяет определить, принадлежит ли точка треугольнику. Вместо использования прямых терминов, в данном абзаце будет обсуждаться общая идея работы алгоритма и его практическая полезность.
Учитывая задачу определения принадлежности точки треугольнику, ведущие специалисты разработали метод, который позволяет эффективно и точно решать данную проблему. Благодаря инновационным решениям и оптимизационным подходам, алгоритм строит математическую модель, которая позволяет проводить проверку с высокой степенью точности и эффективности.
Алгоритм базируется на использовании геометрических принципов и различных математических операций для определения взаимного расположения точки и треугольника. Он учитывает размеры и форму треугольника, а также пространственное положение точки относительно его сторон и углов.
Особое внимание уделено оптимизации алгоритма, чтобы он работал эффективно даже при больших объемах данных. Чтобы достичь высокой производительности, были применены оптимизации вычислений и структур данных, которые сокращают время выполнения алгоритма и улучшают его точность. Разработчики также учли возможность распараллеливания алгоритма для ускорения его работы.
Одним из практических применений данного алгоритма является его использование в компьютерной графике для определения точек, принадлежащих треугольникам, что позволяет строить трехмерные объекты и визуализировать их с высокой степенью точности.
Метод пересечения лучей
Идея метода заключается в следующем: мы выбираем произвольную точку на плоскости и строим из нее лучи в каждую из вершин треугольника. Затем мы подсчитываем количество пересечений этих лучей с ребрами треугольника. Если это количество нечетное, то точка считается принадлежащей треугольнику, а если четное - то точка считается внешней к треугольнику. Этот метод достаточно эффективен и широко используется, так как он позволяет проверить принадлежность точки треугольнику без необходимости вычисления площадей и длин сторон треугольника.
В данном разделе детально рассматривается алгоритм метода пересечения лучей, приводятся примеры его применения и рассматриваются возможные случаи, в которых метод может давать некорректные результаты. Также обсуждаются эффективные способы реализации алгоритма, учитывая особенности задачи и требования к скорости выполнения. Более того, рассматриваются различные модификации метода, учитывающие особенности точки и треугольника, свойства плоскости и пространства.
- Описание метода пересечения лучей
- Правила определения принадлежности точки треугольнику с использованием метода пересечения лучей
- Алгоритм метода пересечения лучей
- Примеры применения метода пересечения лучей
- Возможные проблемы и ограничения метода
- Эффективные способы реализации алгоритма
- Модификации метода пересечения лучей для различных ситуаций
Вопрос-ответ

Какие методы и алгоритмы используются для проверки принадлежности точки треугольнику?
Один из эффективных методов для проверки принадлежности точки треугольнику - это метод с использованием векторных вычислений. Для этого необходимо рассчитать векторы, образованные вершинами треугольника и точкой, которая проверяется на принадлежность. Затем можно использовать векторное произведение этих векторов для определения, находится ли точка внутри треугольника или на его границе.
Как работает метод векторных вычислений для проверки принадлежности точки треугольнику?
Метод векторных вычислений для проверки принадлежности точки треугольнику основан на свойстве векторного произведения. Для каждой стороны треугольника рассчитывается вектор, образованный между двумя вершинами этой стороны и точкой, которая проверяется на принадлежность. Затем выполняется векторное произведение этих векторов. Если все векторные произведения имеют одинаковый знак (положительный или отрицательный), то точка находится внутри треугольника или на его границе.
Какие еще существуют алгоритмы для проверки принадлежности точки треугольнику, кроме метода векторных вычислений?
Помимо метода векторных вычислений, существует также метод барицентрических координат. В этом методе используется представление точки в трехмерном пространстве через ее барицентрические координаты относительно вершин треугольника. При этом проверка принадлежности сводится к определению, лежат ли барицентрические координаты точки в пределах от 0 до 1.
Какие преимущества имеет метод векторных вычислений перед другими алгоритмами?
Метод векторных вычислений обладает несколькими преимуществами по сравнению с другими алгоритмами. Во-первых, он применим для любого треугольника, включая вырожденные случаи, когда стороны треугольника находятся на одной прямой. Кроме того, этот метод является достаточно простым в реализации и вычислительно эффективным, что делает его предпочтительным выбором для проверки принадлежности точки треугольнику.
Какие существуют методы проверки принадлежности точки треугольнику?
Существуют различные методы проверки принадлежности точки треугольнику, включая методы на основе вычисления площади треугольника и методы на основе использования векторов.



