Математика – это одна из науки, которая изучает числа и их взаимосвязи. Это наука о логике и точных расчетах, имеющая широкое применение в различных сферах жизни. В рамках математики, существует множество понятий и формул, которые помогают нам понять и описать окружающий мир.
Угол – это одно из основных понятий геометрии, которое широко используется в различных научных дисциплинах. Углы встречаются повсюду – от естественных объектов, таких как раскрытый цветок, до сложных конструкций и архитектурных форм.
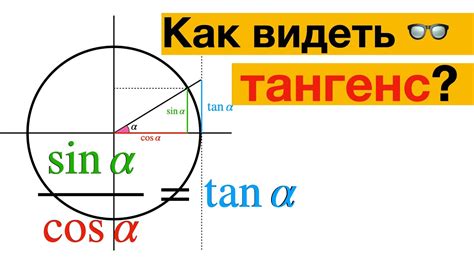
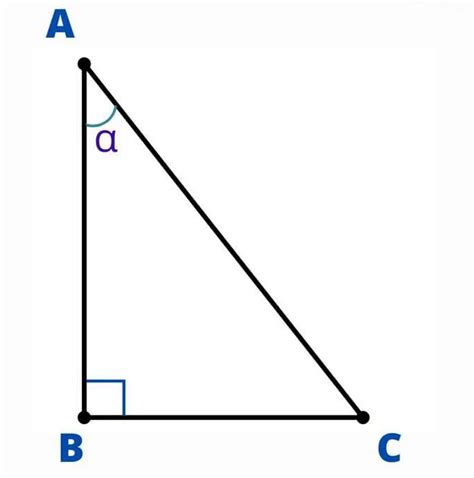
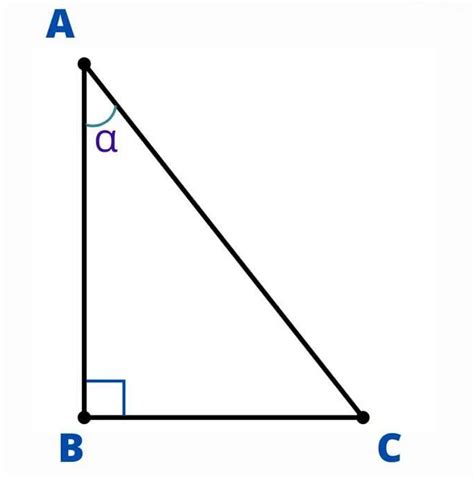
Тангенс угла – это математическая функция, которая помогает нам определить соотношение между двумя сторонами прямоугольного треугольника. Она определяется как соотношение катета противолежащего углу и катета, прилегающего к углу. Данный показатель имеет большое значение в различных областях, таких как физика, инженерия, астрономия и т.д.
Тангенс: определение и свойства
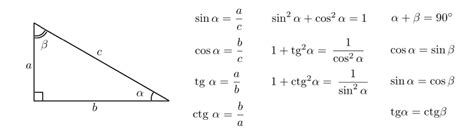
Тангенс угла является отношением противолежащего катета к прилежащему катету в прямоугольном треугольнике. Эта функция широко используется в различных математических и технических расчетах, а также в физике и геометрии. Тангенс позволяет определить угол наклона отрезка или поверхности, а также применяется в решении задач, связанных с треугольниками и прорезями.
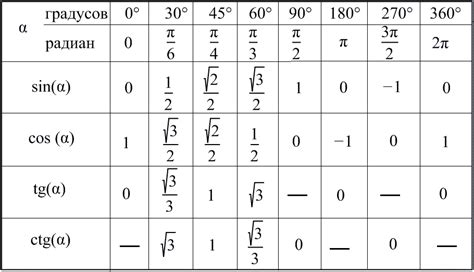
- Тангенс является периодической функцией с периодом π радиан или 180 градусов.
- Значения тангенса могут быть положительными, отрицательными или равными нулю, в зависимости от значения угла, для которого он рассчитывается.
- Тангенс угла 0 равен 0, а тангенс угла 90° или π/2 равен бесконечности.
- Тангенс является нечетной функцией, то есть для отрицательного угла тангенс будет равен противоположному отрицательному значению.
Тангенс имеет множество применений в различных областях. Например, его можно использовать для решения задач оптики, аккуратного расположения объектов в архитектуре или для вычисления градиента на спутниковых снимках. Также тангенс широко применяется в геодезии, навигации, физике и многих других областях науки и техники.
Изучение способов определения значения функции тангенс для угла в 50 градусов
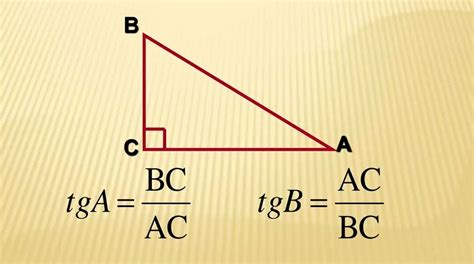
В данном разделе мы рассмотрим методики расчета значений функции тангенс для угла, равного 50 градусов. Будут представлены различные подходы и формулы, позволяющие получить точное значение тангенса данного угла.
Определение значения тангенса угла 50 градусов играет важную роль в различных областях науки и техники. Например, его знание необходимо при проектировании строений, а также при решении задач геометрии и физики. Тангенс угла 50 градусов может быть использован для вычисления длины наклонной стороны треугольника, определения высоты объекта по известной длине тени и других практических задач.
Для нахождения значения тангенса угла 50 градусов существует несколько методов. Одним из самых распространенных является использование таблиц или электронных калькуляторов, где указаны значения тангенса для различных углов. Также можно воспользоваться геометрическим определением тангенса, основанным на отношении сторон прямоугольного треугольника.
Другим методом является применение тригонометрического тождества, позволяющего выразить значение тангенса угла через значение синуса и косинуса. Используя данную формулу, можно вычислить значение тангенса угла 50 градусов.
Познакомившись с разными методами нахождения значения тангенса угла 50 градусов, вы сможете удобно применять их в своих задачах, связанных с геометрией, физикой и другими областями знаний, где требуется расчет данной тригонометрической функции.
| Метод | Описание |
|---|---|
| Использование таблиц и калькуляторов | Получение значения тангенса из предварительно подготовленных таблиц или электронных калькуляторов |
| Геометрическое определение тангенса | Использование отношения сторон прямоугольного треугольника для определения значения тангенса угла |
| Тригонометрическое тождество | Применение формулы, связывающей значение тангенса с синусом и косинусом угла |
Тригонометрические таблицы и вычисление тангенсов
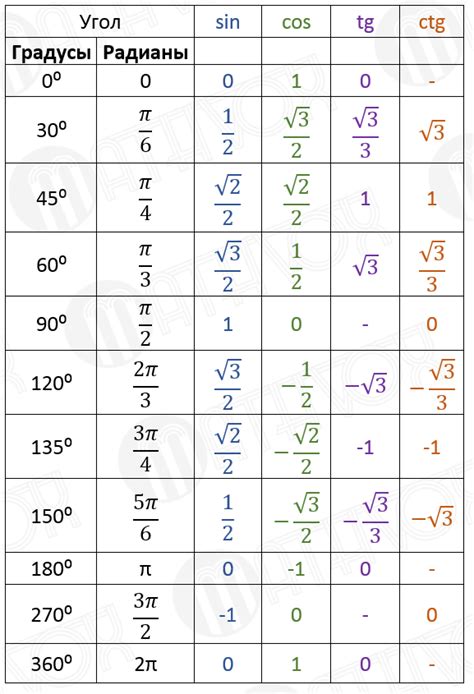
Тригонометрическая таблица представляет собой систематически упорядоченные данные, где для каждого угла указываются соответствующие значения тригонометрических функций. В основе этих таблиц обычно лежит круг, разделенный на равные секторы - градусы, минуты и секунды. Значения тригонометрических функций могут быть представлены в виде десятичных дробей или даже в виде бесконечных периодических десятичных дробей.
Вычисление тангенса угла заключается в нахождении отношения противоположной стороны к прилежащей стороне в прямоугольном треугольнике. Используя данные из тригонометрической таблицы, можно найти точное значение тангенса для разных углов. В прикладных науках и инженерных расчетах это часто используется для определения угла наклона, угла подъема и других величин.
Таким образом, знание тригонометрических таблиц и умение вычислять значение тангенса угла позволяют решать задачи, связанные с треугольниками и плоскими фигурами, определять угловые величины и дополнительные параметры. Это незаменимый инструмент в математике, физике, геометрии, а также в различных сферах строительства и технического проектирования.
Практическое применение тангенса в геометрии

Тангенс - это математическая функция, показывающая соотношение между двумя сторонами треугольника. Он является отношением противоположной стороны к прилежащей стороне угла. Тангенс может быть полезен для определения длины неизвестной стороны треугольника или для вычисления угла между двумя прямыми.
В геометрии тангенс используется для решения различных задач. Например, при проектировании зданий и сооружений, знание тангенса позволяет инженерам и архитекторам определить необходимую высоту и угол наклона крыши, чтобы обеспечить хорошую дренажную систему. Также тангенс используется в навигации, чтобы определить направление и скорость движения объекта.
Еще одним практическим применением тангенса в геометрии является измерение высоты объектов с помощью триангуляции. Триангуляция - это метод определения расстояния или высоты объекта путем измерения углов на треугольнике. Используя тангенс и соответствующие углы, можно вычислить высоту объекта, не прибегая к его прямому измерению.
Таким образом, тангенс является мощным инструментом для решения геометрических задач. Понимание его принципов и правильное использование позволяет решать различные практические задачи в архитектуре, навигации и других областях, где важно знать форму и размер объекта.
Использование тангенса в физике и инженерии
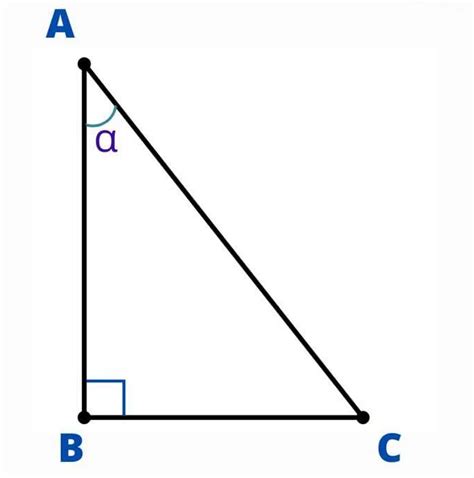
В физике и инженерии тангенс играет важную роль при анализе различных явлений и процессов. Он позволяет определить соотношение между двумя сторонами прямоугольного треугольника и предоставляет возможность измерять углы между этими сторонами. Зная тангенс угла, ученые и инженеры способны более точно предсказывать и объяснять различные явления, что позволяет им разрабатывать оптимальные решения и модели.
Физикам и инженерам приходится использовать тангенс во множестве областей. Например, при проектировании электрических цепей, знание тангенса позволяет определить взаимосвязь между напряжением, силой тока и сопротивлением. Также, при изучении движения объектов на плоскости или в пространстве, тангенс угла наклона позволяет определить скорость и направление движения. Кроме того, тангенс применяется в акустике для анализа звуковых волн и в геодезии для измерения расстояний и высот.
Однако, для эффективного использования тангенса в физике и инженерии необходимо учесть его ограничения и особенности. Например, ошибка в измерении угла может существенно исказить результаты расчетов. Кроме того, тангенс имеет периодическую функцию и может принимать бесконечные значения для некоторых углов. Поэтому, при использовании тангенса следует всегда быть внимательным и учитывать его особенности.
В целом, тангенс играет важную роль в физике и инженерии, предоставляя ученым и инженерам мощный инструмент для анализа, моделирования и прогнозирования различных явлений и процессов. Без него было бы значительно сложнее понять и объяснить множество физических и технических вопросов, которые сегодня решаются с помощью тангенса.
Когда и с какой целью изучать тангенс 50 градусов
К примеру, в физике и инженерии знание тангенса 50 градусов может быть полезно для определения направления силы трения или способности конструкции преодолевать уклоны. Для прогнозирования траектории тела в полете или движения на поверхности, также может потребоваться расчет тангенса 50 градусов.
Тангенс 50 градусов находит применение и в научных исследованиях, в частности, в геофизике и гидрологии, вычисление тангенса позволяет решать задачи о направлении и отклонении потоков, углах наклона поверхности земли или реклации подводных объектов.
Более простыми словами, понимание и умение рассчитывать тангенс 50 градусов может оказаться полезным в различных сферах жизни, например, при выборе оптимальных углов наклона крыши, проектировании скатов дорог или определении величины наклона наклонных катков в забегах.
Применение тангенса в астрономии и навигации
Тангенс, как одна из основных тригонометрических функций, находит свое применение в широком спектре областей, включая астрономию и навигацию. Данная функция позволяет определить соотношение между углом и противолежащей стороной прямоугольного треугольника, что имеет важное значение при изучении и использовании звезд, планет и других небесных тел.
В навигации тангенс применяется для определения дальности и направления движения судна или самолета относительно точки наблюдения, а также для вычисления перекрестных оптических пролетов и определения координат места. Используя тангенс угла наблюдаемой точки и зная длину базовой линии и угол между наблюдателем и объектом, навигаторы могут вычислить дальность до объекта и его точное положение на глобусе.
Практические примеры задач с использованием тангенса 50 градусов
- 1. Пример использования тангенса 50 градусов в строительстве: при расчете длины лестничной пролета или наклона кровли для определения необходимой длины рампы для скейтбордов;
- 2. Пример использования тангенса 50 градусов в геодезии: при определении высоты небоскреба или пролета моста с помощью теодолита;
- 3. Пример использования тангенса 50 градусов в фотографии: при выборе оптимального угла наклона камеры для создания перспективного эффекта или при определении необходимого объектива для съемки панорамного вида;
- 4. Пример использования тангенса 50 градусов в механике: при расчете силы трения или определении угла наклона поверхности, на которой происходит движение;
- 5. Пример использования тангенса 50 градусов в геологии: при расчете угла линейки для определения наклона пластовых слоев или при определении угла наклона зеркала воды при измерении уровня грунтовых вод.
Как видно из данных примеров, тангенс угла 50 градусов имеет широкие приложения в различных областях науки и практики. Расчеты с использованием данной функции тригонометрии позволяют получить точные значения и сделать правильные решения в реальных ситуациях.
Полезные советы для эффективного использования и вычисления тангенса угла
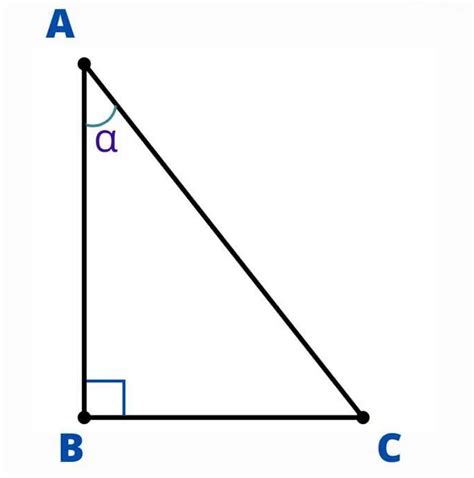
- Составление правильной формулы: прежде чем приступить к расчетам, убедитесь, что вы используете правильную формулу для вычисления тангенса. Например, для вычисления тангенса угла необходимо разделить значение противоположной стороны на значение прилежащей стороны. Правильное использование формулы гарантирует точный расчет тангенса.
- Использование правильных единиц измерения: при работе с тангенсом угла важно использовать правильные единицы измерения. Например, если угол задан в градусах, убедитесь, что ваши вычисления также происходят в градусах. В противном случае, результаты могут быть неточными.
- Учет ограничений: будьте внимательны к ограничениям, связанным с использованием тангенса. Некоторые углы могут иметь определенные ограничения для расчета или не могут быть вычислены с помощью тангенса. Например, тангенс угла 90 градусов не определен, поскольку в этом случае значения противоположной и прилежащей сторон равны нулю.
- Практика и применение: чтобы эффективно использовать тангенс, практикуйтесь на различных задачах и примерах. Чем больше вы будете применять свои знания, тем лучше освоите технику расчетов и понимание тангенса. Используйте тангенс в реальной жизни, например, при оценке наклона крыши или горизонтальной поверхности, а также при решении геометрических задач.
- Использование таблиц и калькуляторов: для более сложных вычислений и операций с тангенсом, вы можете использовать таблицы тангенсов или электронные калькуляторы. Это поможет вам быстро получить значения тангенса для различных углов и применить их в своих расчетах.
Используя указанные советы, вы сможете эффективно использовать тангенс угла в различных ситуациях. Знание и умение правильно применять тангенс поможет вам в решении геометрических задач, а также в применении его в различных научных и инженерных областях.
Практическое применение тангенса 50 градусов: сила подъема в горах
Если вы когда-либо задумывались, как сильная сила тяжести может быть преодолена на подъеме в горы, ответ находится в расчете тангенса 50 градусов. Этот расчет позволяет определить необходимую силу, которую придется приложить для преодоления вертикального уклона в горах.
Тангенс 50 градусов, по сути, является отношением противоположной стороны (высоты вертикального уклона) к прилежащей стороне (горизонтального расстояния). Полученное число из расчета тангенса показывает, насколько вертикальный уклон стоит вам дорого.
В применении к горам, где часто возникают крутые восхождения, расчет тангенса 50 градусов позволяет понять, насколько крутое по отношению к горизонтальной поверхности склон и насколько усилий потребуется для его преодоления. Успешное применение этого расчета помогает планировать восхождения, оптимизировать физическую подготовку и выбирать необходимое снаряжение для успешного покорения высокогорных вершин.
Понимание и применение расчета тангенса 50 градусов может стать полезным инструментом для горных альпинистов, скейтбордистов, велосипедистов и других спортсменов, сталкивающихся с уклонами и восхождениями в своей практике или просто наслаждающихся активным отдыхом на природе.
Вопрос-ответ

Как рассчитать тангенс угла 50 градусов?
Тангенс угла 50 градусов можно рассчитать с помощью тригонометрической функции тангенса. Для этого нужно разделить значение синуса угла на значение косинуса угла. Для угла 50 градусов, синус равен 0.766 и косинус равен 0.643. Итак, тангенс 50 градусов равен 1.19.
Какие примеры использования тангенса угла 50 градусов?
Величина тангенса является важной в различных областях, где требуется работа с углами. Например, в строительстве можно использовать тангенс для расчета высоты здания, зная длину его тени и угол падения солнечных лучей. Также тангенс может быть полезен при решении задач в физике, оптике, геодезии и других науках.
Можно ли рассчитать тангенс угла 50 градусов без использования калькулятора?
Да, тангенс угла 50 градусов можно рассчитать без использования калькулятора, если известны значения синуса и косинуса этого угла. Зная, что тангенс равен отношению синуса к косинусу, можно вручную выполнить несложные арифметические операции и получить результат. В случае угла 50 градусов, синус равен 0.766 и косинус равен 0.643, поэтому тангенс будет равен 1.19.



