Треугольники – одна из основных геометрических фигур, изучаемых в школьной программе. Чтобы понять, что треугольник равнобедренный, необходимо знать его основные свойства и вывести соответствующую формулу. Равнобедренным называется треугольник, у которого две стороны равны друг другу. Такая фигура имеет особые характеристики и уникальные свойства. Чтобы убедиться в равнобедренности треугольника, необходимо провести математические доказательства и рассмотреть примеры.
Чтобы проиллюстрировать концепцию равнобедренности треугольника, рассмотрим несколько примеров. Представим треугольник с основанием, состоящим из двух равных сторон, и катетом, который отличается от них. Из свойства равнобедренного треугольника следует, что основание будет образовывать равные углы с боковыми сторонами. Это значит, что противолежащие углы при основании также будут равными. Таким образом, мы можем убедиться, что треугольник является равнобедренным, используя геометрические доказательства и примеры.
Математические доказательства равнобедренности треугольника

Одно из самых простых и распространенных доказательств равнобедренности треугольника основано на свойстве углов при основании.
Свойство углов при основании утверждает, что если в треугольнике две стороны равны, то их противолежащие при основании углы также равны.
Доказательство:
- Пусть треугольник ABC равнобедренный, то есть AB = AC.
- Проведем биссектрису угла BAC и обозначим точку пересечения с основанием треугольника как D.
- Рассмотрим треугольники ABD и ACD. У них две стороны равны: AB = AC и AD – общая сторона.
- По свойству углов при основании получаем, что углы B и C равны: ∠ABD = ∠ACD.
- Таким образом, треугольник ABC является равнобедренным, так как он имеет две равные стороны AB и AC и равные углы B и C при основании.
Таким образом, математические доказательства равнобедренности треугольника являются важной частью геометрии и помогают нам установить свойства и отношения между сторонами и углами треугольника.
Доказательство по свойству равенства двух сторон и углов
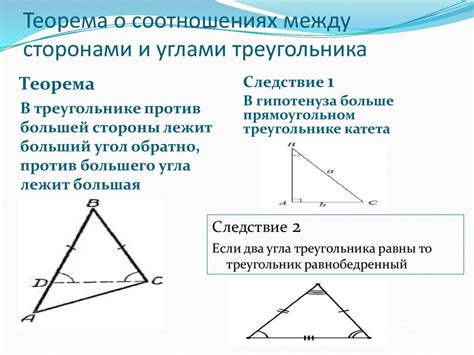
Для того чтобы доказать, что треугольник равнобедренный, необходимо и достаточно показать, что у него равны две стороны и два угла. Рассмотрим этот вопрос более детально.
Свойство равенства двух сторон в равнобедренном треугольнике:
- Задан треугольник ABC, в котором AB=AC.
- Проводим биссектрису угла BAC и обозначаем ее точкой D.
- Так как AD является биссектрисой угла BAC, то AD делит угол BAC пополам.
- По свойству биссектрисы, BD=DC.
- Так как AB=AC и BD=DC, то треугольник ABD равнобедренный.
- Аналогично, треугольник ACD также является равнобедренным.
- Таким образом, треугольник ABC является равнобедренным, так как в нем равны две стороны AB и AC.
Свойство равенства двух углов в равнобедренном треугольнике:
- Треугольник ABC, в котором AB=AC, является равнобедренным.
- Пусть угол BAC является равным углу BCA.
- Проведем биссектрису угла BAC и обозначим ее точкой D.
- Так как AD является биссектрисой угла BAC, то AD делит угол BAC пополам.
- Угол BAD тогда равен углу CAD.
- Так как AB=AC и угол BAD равен углу CAD, то треугольник ABD равен треугольнику ACD по двум сторонам и углу.
- Аналогично, треугольник ACD равен треугольнику ABD.
- Таким образом, угол BCA также является равным углу ABC, и треугольник ABC равнобедренный.
Доказательство с помощью медианы и биссектрисы
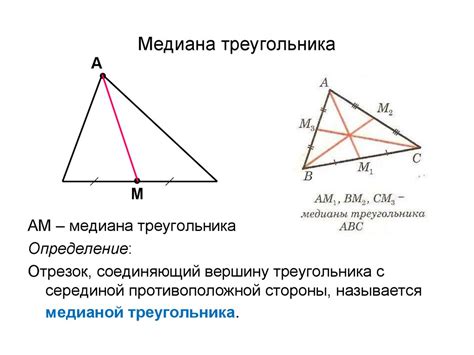
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Если треугольник равнобедренный, то медиана, проведенная из вершины к основанию, будет равна половине длины равных сторон треугольника.
Биссектриса треугольника - это отрезок, который делит угол треугольника на два равных угла. Если треугольник равнобедренный, то биссектриса, проведенная из вершины к основанию, будет делить основание на две равные части.
Таким образом, чтобы доказать, что треугольник равнобедренный, нужно проверить, что медиана, проведенная из вершины к основанию, равна половине длины равных сторон, и что биссектриса, проведенная из вершины к основанию, делит основание на две равные части.
Для наглядности, можно рассмотреть пример равнобедренного треугольника ABC, где AB=AC:
AB = AC
Проведем медиану BD из вершины B к середине основания AC. Если треугольник равнобедренный, то медиана BD будет равна половине длины стороны AC:
BD = 1/2 * AC
Также проведем биссектрису BE из вершины B к основанию AC. Если треугольник равнобедренный, то биссектриса BE будет делить основание AC на две равные части:
AE = EC
Таким образом, если медиана BD равна 1/2 стороны AC и биссектриса BE делит основание AC на две равные части, то треугольник ABC является равнобедренным.
Доказательство с использованием высоты и смежных углов
Шаг 1: Пусть у нас есть треугольник АВС.
Шаг 2: Проведем высоту СD, перпендикулярную стороне АВ.
Шаг 3: Известно, что высота треугольника является перпендикуляром к основанию, а значит, угол АCD и угол ВCD являются прямыми углами.
Шаг 4: Поскольку угол АCD является прямым углом и угол ABC является смежным углом с углом АCD, то угол ABC также является прямым.
Шаг 5: Также известно, что угол ВCD является прямым углом и угол BCA является смежным углом с углом ВCD, следовательно, угол BCA также является прямым.
Шаг 6: Таким образом, у нас получаются два прямых угла в треугольнике АВС, что говорит о том, что треугольник является равнобедренным.
Таким образом, доказывается математическим путем, что треугольник АВС является равнобедренным, используя высоту и смежные углы.
Примеры равнобедренных треугольников

Пример 1: Равнобедренный треугольник со сторонами длиной 5 см, 5 см и 7 см.
Доказательство: В данном треугольнике две стороны равны 5 см, что означает равенство двух углов треугольника. Значит, треугольник равнобедренный.
Пример 2: Равнобедренный треугольник со сторонами длиной 8 см, 8 см и 10 см.
Доказательство: В этом треугольнике две стороны равны 8 см, что означает равенство двух углов треугольника. Значит, треугольник равнобедренный.
Примеры равнобедренных треугольников помогают понять, какие условия должны быть выполнены для определения треугольника как равнобедренного.
Примеры равнобедренности в природе

Равнобедренные треугольники могут быть найдены не только в мире математики, но и в самой природе. Вот несколько примеров, которые иллюстрируют эту удивительную особенность:
Крыло бабочки. Многие виды бабочек имеют равные боковые стороны своих крыльев. Это является примером природной равнобедренности и позволяет бабочкам легко маневрировать в воздухе.
Тело муравья. В основании тела муравья можно найти равные стороны. Это дает им большую стабильность и эффективность при передвижении в поисках пищи и защите своей колонии.
Цветок подсолнуха. Семена подсолнуха расположены на круглой головке, которая имеет форму равнобедренного треугольника. Это позволяет семенам быть равномерно размещенными и получать максимальное количество солнечного света.
Желудь. У желудя также есть форма равнобедренного треугольника. Это помогает ему легко прокатываться по земле и распространять свои семена.
Таким образом, равнобедренные треугольники не только представляют интерес с математической точки зрения, но и являются важным аспектом в различных аспектах живой природы.
Примеры равнобедренности в архитектуре

Геометрические принципы равнобедренности часто находят отражение в архитектуре. Здания и сооружения, строящиеся с учетом этих математических принципов, приобретают особую гармонию и эстетическую привлекательность.
Один из ярких примеров равнобедренного треугольника в архитектуре – это пирамиды Древнего Египта. Благодаря равенству двух боковых сторон треугольника, пирамиды имеют стройную и устойчивую форму, выгодно выделяющуюся на фоне окружающего ландшафта.
Еще одним примером равнобедренности в архитектуре являются готические соборы с их изящными шпилями и башнями. Благодаря равным углам между крышками башен и равным боковым сторонам, здания приобретают величественный и асимметричный вид.
Современная архитектура также часто использует принцип равнобедренности. Например, в высотных небоскребах можно наблюдать равнобедренные треугольные формы. Они обеспечивают прочность и устойчивость сооружений, а также придают им современный и динамичный облик.
Таким образом, равнобедренность – важный математический принцип, который находит свое применение в архитектуре. Благодаря учету этого принципа, здания и сооружения приобретают эстетическую привлекательность и выделяются на фоне окружающего пространства.
Примеры равнобедренных треугольников в геометрии
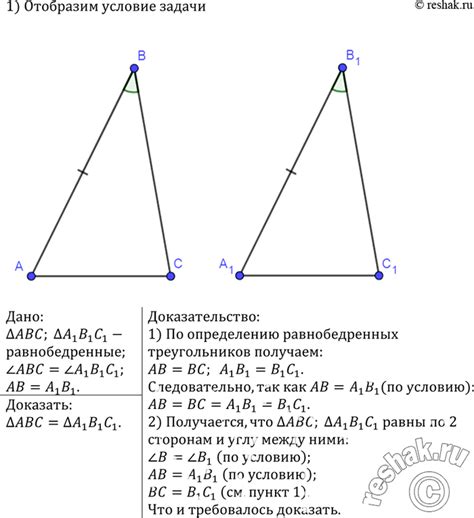
1. Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, у которого две стороны равны. Такой треугольник имеет два равных угла напротив равных сторон. Равные стороны треугольника называются бедрами, а основание – третья сторона.
Пример равнобедренного треугольника:
AB = AC
∠B = ∠C
2. Равнобедренный прямоугольный треугольник
Равнобедренный прямоугольный треугольник – это треугольник, у которого угол около прямого угла равен 45 градусов, а две катеты при прямом угле равны.
Пример равнобедренного прямоугольного треугольника:
AB = AC
∠B = ∠C = 45°
3. Равнобедренный равносторонний треугольник
Равнобедренный равносторонний треугольник – это треугольник, у которого все три стороны равны. Такой треугольник имеет три равных угла величиной по 60 градусов.
Пример равнобедренного равностороннего треугольника:
AB = AC = BC
∠A = ∠B = ∠C = 60°
Эти примеры демонстрируют различные типы равнобедренных треугольников, которые можно встретить в геометрии. Знание этих примеров поможет лучше понять свойства и особенности равнобедренных треугольников и использовать их в решении математических задач.