Один из важных аспектов статистического анализа данных - это глубина выборки, которая позволяет получить информацию о характеристиках всей выборки. В данной статье мы рассмотрим понятие глубины выборки четверти и ее влияние на статистический анализ данных.
Глубина выборки четверти – это параметр, который указывает на размер выборки четверти от общего объема выборки. Важно отметить, что выборка четверти представляет собой особую часть выборки, которая включает 25% наиболее репрезентативных данных. Таким образом, глубина выборки четверти позволяет нам получить информацию о значимых данных, играющих важную роль в анализе данных.
При проведении статистического анализа данных, глубина выборки четверти имеет решающее значение. Большая глубина выборки четверти позволяет получить более точные и достоверные результаты анализа. Однако, вместе с возрастанием глубины выборки четверти возрастает объем исследуемых данных, что может потребовать дополнительных вычислительных ресурсов и времени.
Влияние глубины выборки четверти на статистический анализ
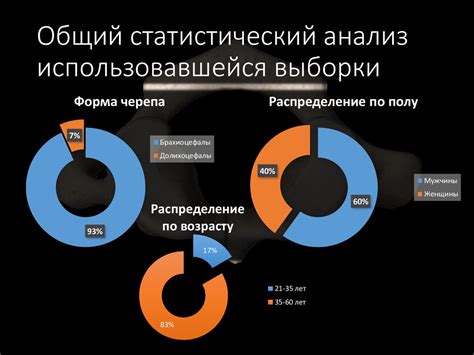
Большая глубина выборки четверти обеспечивает более точные оценки характеристик и параметров генеральной совокупности. Чем больше наблюдений участвует в анализе, тем больше уверенность в полученных результатах. Таким образом, при большой глубине выборки четверти статистический анализ имеет высокую степень точности и достоверности.
Однако, при выборе глубины выборки четверти необходимо учитывать как числовые, так и временные ресурсы, необходимые для проведения исследования. Слишком большая выборка может потребовать значительных затрат, как финансовых, так и временных. Поэтому, оптимальная глубина выборки четверти должна быть сбалансирована, учитывая цель исследования, наличие ресурсов и желаемый уровень точности.
Четверть в статистическом анализе данных
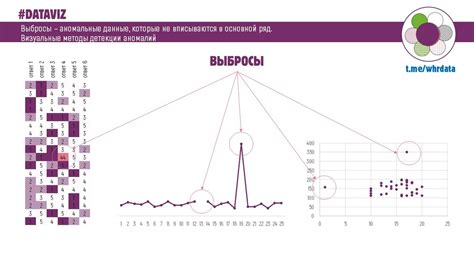
Главная цель использования квартилей - определить, как распределены данные внутри выборки. Четверти могут дать представление о том, где находятся средние значения и какие значения являются выбросами.
Существует 3 квартили: первый (Q1), медиана (Q2) и третий (Q3). Первый квартиль (Q1) разделяет выборку на две равные части - 25% значений находятся слева от Q1, а оставшиеся 75% значений - справа от Q1. Медиана (Q2) делит выборку на две равные части - 50% значений находятся слева от Q2, а оставшиеся 50% значений - справа от Q2. Третий квартиль (Q3) разделяет выборку на две равные части - 75% значений находятся слева от Q3, а оставшиеся 25% значений - справа от Q3.
Четверть важна в статистическом анализе данных, поскольку она помогает определить меру разброса значений. Распределение данных может быть симметричным или асимметричным, а четверти позволяют наглядно выявить эти особенности.
Кроме того, четверти могут быть использованы для определения выбросов и экстремальных значений. Если значение данных находится за пределами 1,5 межквартильного размаха (разницы между третьим квартилем и первым квартилем), оно считается выбросом и может быть исключено из анализа.
Значимость глубины выборки четверти
Важно понимать, что глубина выборки четверти должна быть достаточно большой для достоверности результатов. Оптимальным размером выборки считается такой, при котором обеспечивается приемлемая точность оценок, приемлемая степень погрешности и учитывается размер генеральной совокупности.
Подсчет глубины выборки четверти осуществляется с помощью различных методов, таких как формулы и таблицы. Важно учитывать цель исследования, характеристики генеральной совокупности и другие факторы при выборе оптимального значения глубины выборки.
Применение глубины выборки четверти в практике
Глубина выборки четверти выступает важным инструментом при проведении статистического анализа данных. Этот показатель определяет количество наблюдений, которые охватывают только первую или последнюю четверть данных. Он позволяет более точно изучать распределение данных и выявлять статистические закономерности.
Применение глубины выборки четверти на практике может быть полезным во многих областях, включая экономику, финансы, медицину и маркетинг. Например, в медицине глубина выборки четверти может использоваться для изучения распределения времени выздоровления пациентов или для оценки эффективности лекарственных препаратов. В экономике и финансах этот показатель может помочь в анализе доходности инвестиций или оценке риска.
Кроме того, глубина выборки четверти может быть полезна при анализе социальных исследований или обработке больших объемов данных. Она помогает сократить объем выборки без значительной потери информации, что может быть полезно при ограниченных ресурсах или для более эффективного анализа данных.
Важно отметить, что применение глубины выборки четверти требует аккуратного подхода и анализа. Неправильное определение глубины выборки может привести к искажению результатов и неверной интерпретации данных. Поэтому рекомендуется проводить дополнительные исследования и консультироваться с опытными специалистами перед применением данного метода.