Наука никогда не прекращает своего изучения, и каждый шаг вперед открывает перед нами новые горизонты познания. В этом непрерывном стремлении расширить свои знания мы встречаемся с разнообразными явлениями и закономерностями, которые описывают мир вокруг нас. Одним из таких увлекательных исследований является изучение периодичности функций и их влияния на наше понимание окружающей действительности.
Сегодня наш взгляд обращается к одной из самых удивительных функций, которая привлекает внимание своей особой периодичностью и гармонией. Эта функция известна как cos2(x) – математическое выражение, построенное на основе косинуса. В отличие от изначального косинуса, функцию cos2(x) отличает несколько особенностей, которые делают ее уникальной и позволяют нам погрузиться в удивительный мир ее периодичности.
Переплетение силы и красоты заключено в уравнении cos2(x), где x представляет собой переменную, которая влияет на форму графика функции. Математические выкладки показывают, что периодичность cos2(x) начинается с минимального положительного значения, что вызывает особый интерес у исследователей. В этом контексте мы восхищаемся гармоничными колебаниями функции и стремимся раскрыть все ее тайны, которые отражают естественную периодичность окружающего мира.
Определение функции cos2(x)

В данном разделе мы рассмотрим основные характеристики функции cos2(x) и попытаемся определить ее особенности и влияние на математические модели и задачи.
Функция cos2(x) является квадратом функции косинуса, что означает, что она принимает значения, равные квадрату значений функции косинуса при тех же аргументах. Периодичность функции cos2(x) также зависит от периодичности функции косинуса, что делает ее цикличной и регулярной.
Важным свойством функции cos2(x) является ее неотрицательность на всей числовой прямой, так как квадрат значения функции косинуса всегда неотрицательный. Это свойство позволяет использовать функцию cos2(x) в различных задачах, где требуется работать только с положительными значениями.
Функция cos2(x) имеет возможность моделировать периодические и колебательные процессы в различных областях науки и техники. Например, она может описывать колебания в физических системах, электрические сигналы в электронике или изменение освещенности в оптических системах.
Исследование и понимание функции cos2(x) позволяет анализировать ее влияние на задачи различной природы, оптимизировать и находить решения с использованием данной функции. Кроме того, она также является важным элементом при изучении математических моделей и исследовании их свойств.
Периодичность функции косинус величины в квадрате
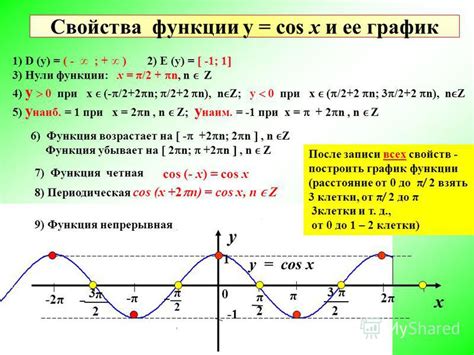
Этот раздел посвящен периодичности функции, которая представляет собой косинус квадрата переменной величины. Мы исследуем, как эта функция повторяется с течением времени и как ее значения изменяются по мере прохождения определенных интервалов.
Периодичность - это характеристика функции, которая означает, что ее значения повторяются через определенные интервалы. В данном случае мы рассматриваем периодичность функции косинус величины в квадрате, что означает, что ее значения будут повторяться через определенное количество времени или через определенные интервалы значений аргумента.
Изучение периодичности функции cos2(x) поможет нам понять, как она повторяет свое значение и какие интервалы следует рассматривать при анализе ее изменений. Мы будем исследовать, какие значения функции повторяются через определенные интервалы времени и какие закономерности можно выявить в ее поведении.
График функции косинус в квадрате от аргумента
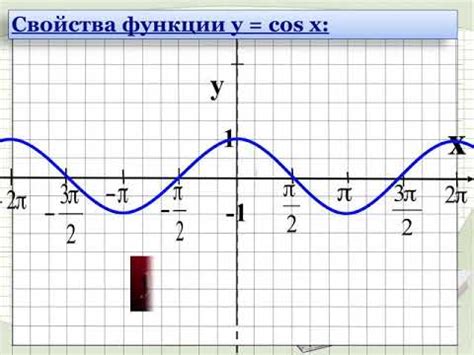
График функции cos2(x) характеризуется периодичностью, что означает, что он повторяется через определенные промежутки. Для построения графика необходимо выбрать некоторый интервал значений для аргумента и рассчитать соответствующие значения функции для каждой точки на этом интервале. Затем, на координатной плоскости отмечаются эти точки и соединяются линией.
Знание графика функции cos2(x) позволяет легко определить особенности данной функции, такие как значения наименьшего положительного периода, максимальные и минимальные значения функции, а также ее поведение при изменении аргумента. График является важным инструментом для визуализации и анализа функций, что помогает в изучении их свойств и характеристик.
Малейший цикл функции косинус в квадрате от переменной x

Рассмотрим важный аспект функции, в которой применяется косинус. Будем исследовать свойства функции, которая возводит переменную в квадрат и затем находит ее косинус. Основной интерес состоит в определении наименьшего положительного временного интервала, в течение которого функция повторяется, то есть происходит полный цикл процесса. Данный интервал поможет понять, какой минимальный угол необходимо пройти, чтобы функция приняла значение, аналогичное одному из предыдущих значений.
При изучении данной функции с точки зрения периодичности, возникают ключевые вопросы исследования: а) как изменяется функция с увеличением значения x, и б) каков промежуток, который функция должна пройти, чтобы получиться в исходное положение. Целью исследования является определение наименьшего положительного периода, то есть временного интервала, который требуется функции, чтобы вернуться к своему начальному состоянию. Задачей является выявление угла, который соответствует этому периоду и описывает весь цикл повторения.
Для более точного изучения функции cos2(x) мы проводим анализ ее свойств и строим график, чтобы наглядно увидеть, как происходит циклическое изменение функции в зависимости от значения x. При исследовании наименьшего положительного периода появляются ключевые моменты, такие как моменты симметрии функции и пересечения графика с осью абсцисс.
Решение уравнений cos2(x) = a

Для начала, заметим, что в данном уравнении угол x находится внутри функции косинуса в виде его аргумента. Для решения этого уравнения необходимо найти такие значения угла x, при подстановке которых значение cos2(x) станет равным заданному значению a.
Один из способов решения данного уравнения - использование формулы двойного угла для функции косинус. Согласно этой формуле, cos2(x) можно представить в виде выражения, содержащего cos(x) и sin(x). Приравнивая полученное выражение к a, мы получаем новое уравнение, в котором участвуют sin(x) и cos(x).
Далее можно воспользоваться другими методами решения системы уравнений, такими как замена переменных, использование тригонометрических тождеств и тригонометрической окружности. Эти методы позволяют найти все возможные решения уравнения cos2(x) = a и выяснить, какие значения переменной x удовлетворяют данному равенству.
В завершение обратим внимание на то, что значения аргумента x в уравнении cos2(x) = a могут быть ограничены определенным интервалом. Также, в зависимости от значения a, могут возникать особые случаи, требующие отдельного рассмотрения и специфических подходов к решению.
Практическое применение изучения мельчайшего положительного цикла функции cos2(x)
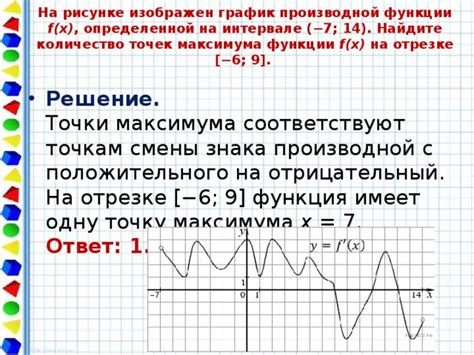
Астрономия и астрофизика: В изучении движения небесных тел важно точно определить их периоды, чтобы предсказывать их положение и фазы в будущем. Изучение наименьшего положительного цикла функции cos2(x) может помочь в определении точного времени обращения планеты вокруг Солнца, а также передвижения комет, астероидов и других небесных объектов.
Физика и инженерия: Во многих физических системах и инженерных конструкциях имеются циклические движения или изменения параметров. Изучение наименьшего положительного цикла функции cos2(x) может помочь определить время колебаний в системах с механическими, электрическими или оптическими элементами. Это полезно для расчета энергетической эффективности, проектирования надежных систем и обнаружения неисправностей.
Финансы и экономика: В финансовом анализе и прогнозировании рыночных циклов используются математические модели, основанные на периодических функциях. Изучение наименьшего положительного цикла функции cos2(x) может помочь в анализе временных рядов финансовых данных, таких как цены на акции, фондовые индексы или валютные курсы. Это позволяет идентифицировать циклические закономерности, предсказывать будущие тренды и принимать рациональные финансовые решения.
Таким образом, практическое применение изучения наименьшего положительного периода функции cos2(x) охватывает широкий спектр областей, включая астрономию, физику, инженерию, финансы и экономику. Понимание и использование циклических паттернов помогает улучшить точность прогнозирования и оптимизацию процессов в различных системах и сферах деятельности.
Вопрос-ответ

Какое значение имеет исследование наименьшего положительного периода функции cos2(x)?
Исследование наименьшего положительного периода функции cos2(x) позволяет выяснить, через какой промежуток x функция проходит полный цикл повторения значений.
Как найти наименьший положительный период функции cos2(x)?
Наименьший положительный период функции cos2(x) можно найти, разделив период функции cos(x) на 2.
Зачем исследовать наименьший положительный период функции cos2(x)?
Исследование наименьшего положительного периода функции cos2(x) помогает определить, какой отрезок x необходимо рассмотреть для полного охвата всех возможных значений функции.
Какие значения может принимать функция cos2(x)?
Функция cos2(x) может принимать значения от 0 до 1, так как это квадрат косинуса значения x.
Какие основные свойства имеет функция cos2(x)?
Основными свойствами функции cos2(x) являются периодичность с периодом, равным половине периода функции cos(x), и ограниченность сверху значением 1.



