Сила, энергия, масса... Знакомы и понятны. Но как они измеряются, представляются и описываются? Какими символами и числами мы их обозначаем?
Разнообразие математических обозначений, используемых для выражения физических величин и чисел, просто поражает воображение. Но за этой разнообразностью скрываются глубокие смыслы и тайны, которые раскрываются лишь знатокам искусства превращения абстрактных понятий в конкретные числа.
Почему одни величины обозначаются цифрами, а другие – буквами? Каковы принципы присвоения значений и обозначений? И зачем нам эти символы и числа в нашей жизни?
Определение и примеры феноменов природы, которые можно измерить

Физические явления и процессы, окружающие нас, могут быть описаны с помощью различных физических величин. Они позволяют измерять и оценивать разнообразные характеристики природы. В этом разделе мы рассмотрим конкретные примеры физических величин и их значений, которые помогают нам понять и описать многообразие феноменов, происходящих вокруг нас.
Температура – это физическая величина, которая отражает степень нагретости объекта. Она может быть измерена с помощью термометра и выражается в градусах Цельсия или Фаренгейта. Примерами температуры могут служить показательный столбец термометра, ощущаемая холодность льда или жар от пламени свечи.
Скорость – это физическая величина, определяющая изменение положения объекта за единицу времени. Она может быть измерена с помощью специальных приборов, например, скоростомера или спидометра. Примерами скорости могут быть различные виды передвижения, такие как бег, езда на велосипеде или движение автомобиля.
Масса – это физическая величина, показывающая количество вещества в объекте. Она измеряется с помощью весов и выражается в килограммах или других единицах массы. Примерами массы могут быть металлический блок, плод или животное, которые можно сравнить по их относительной тяжести.
Таким образом, физические величины являются неотъемлемой частью нашего понимания мира. Они помогают описать и измерить разнообразные явления природы, облегчая наше взаимодействие с окружающей средой и позволяя нам углубить наше знание о нашей вселенной.
Важные свойства и особенности физической величины
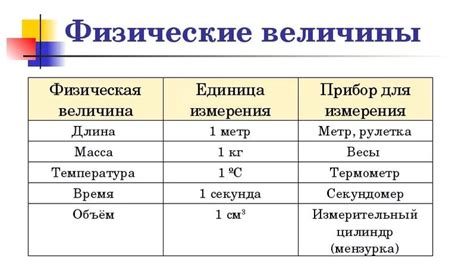
Свойства и особенности изучаемых в физике величин имеют высокую значимость для понимания и описания различных явлений и процессов в природе и науке. Путем анализа разных физических величин, мы можем получить углубленное понимание их назначения и роли в системе изучения объективной реальности.
Измерение и меры: понятия и подходы

Измерение является неотъемлемой частью физики и других естественных наук, а также обыденной жизни. Оно позволяет оценить количество или степень существующей физической величины, например, длины, массы, времени и других характеристик объектов и явлений. Подходы к измерению могут варьироваться в зависимости от научной дисциплины и поставленных задач. Однако общей целью измерения является получение количественных данных, которые позволяют описать и анализировать происходящие процессы, сравнивать различные объекты и явления, а также прогнозировать их поведение.
В процессе измерения необходимо использовать единицы измерения - определенные стандартные значения, которые служат основой для количественных оценок. Единицы измерения могут быть абсолютными (например, метр, килограмм, секунда) или относительными (например, проценты, градусы). Они позволяют перевести физическую величину в числовой вид, который более удобен для обработки и сравнения.
В различных областях науки и практики применяются различные системы и единицы измерения. Например, в системе Международной системы единиц (СИ) основными единицами измерения являются метр, килограмм, секунда и др. Также существуют специфические единицы измерения для разных физических величин, такие как градус Цельсия, ампер, моль и др. Необходимость использования конкретных единиц измерения обусловлена характером изучаемых объектов и задачами, стоящими перед исследователями и практиками.
| Наименование | Обозначение | Примеры физических величин |
|---|---|---|
| Метр | м | Длина, высота, расстояние |
| Килограмм | кг | Масса |
| Секунда | с | Время |
| Ампер | А | Электрический ток |
Точность и погрешность измерений
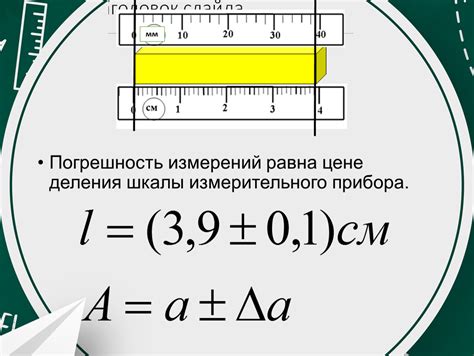
Когда мы измеряем физические величины или числа, мы всегда стремимся к наибольшей точности. Однако, любое измерение неизбежно сопровождается погрешностью, которая может возникать из различных причин.
Точность измерения - это способность получить значение близкое к истинному значению величины или числа. Она напрямую связана с понятием погрешности. Погрешность измерения - это расхождение между измеренным значением и его истинным значением.
Погрешность может быть вызвана как систематическими, так и случайными факторами. Систематическая погрешность обусловлена ошибками прибора или методики измерения и всегда приводит к постоянному смещению результатов в одну и ту же сторону. Случайная погрешность возникает из-за непредсказуемых внешних факторов и характеризуется случайным отклонением результатов в разных направлениях.
Для оценки точности и погрешности измерений часто используют статистические методы. Например, через среднюю арифметическую погрешность можно определить дисперсию и стандартное отклонение результатов измерений. Эти характеристики позволяют оценить степень разброса измерений и контролировать качество полученных данных.
Понимание и учет точности и погрешности измерений играют важную роль в различных областях, таких как наука, техника, медицина и многие другие. От правильной оценки и учета погрешностей зависит достоверность результатов и последующий анализ данных.
Векторные и скалярные величины

В данном разделе рассматриваются два основных типа физических величин: векторные и скалярные. Векторные величины имеют направление и величину, тогда как скалярные величины характеризуются только численным значением. Обладая различными характеристиками и значениями, эти типы величин играют важную роль в физике и других научных областях.
Выделяясь своими особенностями, векторные величины имеют не только численное значение, но и направление, которое можно представить в виде стрелки или вектора. Они полностью определяются своей величиной, направлением и точкой приложения. Примерами векторных величин могут служить скорость, сила, ускорение, импульс и другие физические величины, которые требуют указания направления для полного описания.
Скалярные величины, в отличие от векторных, характеризуются только численным значением и не имеют направления. Они описываются только одним числом, которое указывает на их величину. Примерами скалярных величин могут служить масса, время, длина, температура и другие параметры, коим не требуется указание направления для полного описания.
Различие между векторными и скалярными величинами имеет фундаментальное значение в физике и других научных дисциплинах. Их правильное понимание и использование позволяют более точно и полнохарактеризовать и анализировать различные явления и процессы в природе.
- Векторные величины имеют не только величину, но и направление.
- Скалярные величины характеризуются только численным значением, без указания направления.
- Примеры векторных величин: скорость, сила, ускорение, импульс.
- Примеры скалярных величин: масса, время, длина, температура.
Число в физике: сущность и важность
Числа играют важную роль в физике, позволяя описывать и измерять различные явления и свойства природы. Они представляют собой абстрактные математические конструкции, которые применяются для измерения величин, определения закономерностей и предсказания результатов экспериментов.
В физике число может быть использовано для измерения физических величин, таких как масса, скорость, сила, энергия и т.д. Оно может обозначать как конкретные значения, так и абстрактные величины, которые позволяют описать состояние объектов и их взаимодействия.
Кроме того, число может использоваться для выражения математических законов и фундаментальных констант в физике. Например, число Пи (π) является одной из таких констант и используется для вычисления длин окружности, площадей и объемов различных фигур. Также число Ейлера (e) и число Гравитационной постоянной (G) имеют важное значение в различных физических теориях.
Важно отметить, что число в физике не просто является инструментом для измерений, но также является фундаментальным элементом в построении научных моделей и объяснении природных явлений. Числа помогают сформулировать законы, установить связи между различными явлениями и создать целостную картину мира в рамках научной дисциплины.
Арифметические и математические операции с физическими величинами

В физике неразрывно связаны численные значения и математические операции. Операции над физическими величинами позволяют проводить различные расчеты и получать новые значения, отражающие изменения в системе.
При выполнении арифметических операций с физическими величинами важно учитывать их размерность и единицы измерения. Это позволяет сохранить консистентность и точность результатов. Кроме того, при выполнении операций необходимо учитывать правила соответствующих математических операций.
- Сложение и вычитание физических величин проводятся с учетом их размерности и единиц измерения. В результате получается величина с той же размерностью и единицами измерения.
- Умножение и деление физических величин также учитывают размерность и единицы измерения. Результатом умножения или деления является величина с соответствующей размерностью и новыми единицами измерения.
- Возведение в степень и извлечение корня из физических величин требуют особого внимания к размерности и единицам измерения. Результаты таких операций могут быть выражены как величина с новой размерностью и новыми единицами измерения.
Правильное применение арифметических и математических операций в физике позволяет получать новые значения физических величин и использовать их для решения различных задач и расчетов.
Математические константы и их сущность в физике
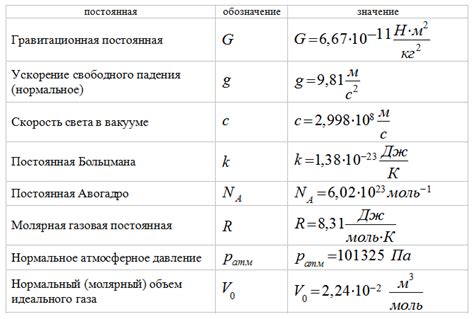
Известно, что в физике существуют математические константы, которые играют значимую роль в решении различных задач. Эти числа не только имеют фундаментальное значение в математике, но и находят свое применение в различных областях науки, включая физику.
Одной из таких констант является число π. Точное значение этой иррациональной математической константы, обозначающей отношение длины окружности к ее диаметру, было исследовано учеными на протяжении многих веков. Значение π округляется до 3.14159 и является важным элементом в множестве формул и уравнений физики. Оно применяется для расчета площадей, объемов, количества вращений и других физических величин.
Еще одной важной математической константой является число e. Экспоненциальная константа e является базой натурального логарифма, и она появляется во многих математических моделях, используемых в физике. Значение числа e равно примерно 2.71828 и оно используется для описания экспоненциального роста и затухания, а также для вычисления вероятностей и стохастических процессов.
Кроме того, магнитная постоянная является важным математическим значением в физике. Она обозначается символом μ₀ и представляет собой физическую величину, связанную с взаимодействием магнитных полей и токов. Значение магнитной постоянной составляет 4π × 10⁻⁷ Н/А² и используется для вычисления силы между проводниками с током и магнитным полем, а также для определения магнитных свойств различных материалов.
Таким образом, значения математических констант в физике помогают ученым и инженерам создавать точные модели и предсказывать результаты экспериментов. Понимание этих констант и их использование являются фундаментальной частью физической науки и помогают расширить наше понимание мира вокруг нас.
Вопрос-ответ

Что такое физическая величина и число?
Физическая величина - это характеристика материального объекта, явления или процесса, которая может быть количественно измерена. Физическое число - это числовое значение, которое отражает величину физической величины.
Какие основные характеристики физических величин?
Основными характеристиками физических величин являются размерность, измеряемость, скалярность или векторность, и операционный способ задания.
Что представляет собой размерность физической величины?
Размерность физической величины - это способ представления ее количественных характеристик с помощью комбинации базовых единиц измерения. Например, размерность скорости может быть представлена в метрах в секунду (м/с).
Чем отличаются скалярные и векторные физические величины?
Скалярные физические величины характеризуются только числовым значением и единицами измерения, например, масса или температура. Векторные физические величины, такие как сила или скорость, имеют не только числовое значение, но и направление и точку приложения.



