Погрузившись в мир алгебры, мы открываем перед собой целый океан возможностей. Эта наука как ключ, открывающий для нас ворота в увлекательный мир чисел, формул и уравнений. В каждом разделе алгебры мы встречаем новые методы, способы решения, которые помогают нам найти ответы на самые изощренные головоломки.
Быть хорошим алгебраистом - значит обладать не только глубоким пониманием материала, но и уметь применять различные подходы к решению задач. Именно поэтому каждый школьник должен расширять свой арсенал методов, чтобы стать настоящим экспертом в алгебре. Независимо от того, какие задачи нам предстоит решать - сложные или простые, абстрактные или практические - всегда можно найти подходящий метод, который поможет нам добиться успеха и получить верное решение.
Когда мы сталкиваемся с математической задачей, наш ум начинает работать на полную мощность, и в этот момент мы подключаем все свои знания и навыки. Алгебра - это не просто набор формул и правил, это настоящее искусство преобразования чисел и символов. И в этом искусстве существуют свои инструменты и методы, которые помогают нам оперативно решать задачи. Некоторые из них основаны на применении логического мышления, другие - на использовании готовых алгоритмов и мнемонических правил. Каждый из них имеет свои преимущества и подходит для решения определенного типа задач.
Определение условия задачи и символическое обозначение неизвестных

Этот раздел познакомит вас с основными шагами по разбору условия задачи, позволит избегать недоразумений при описании проблемы и предложит подходы к формулировке неизвестных величин. Такой подход обеспечивает ясность и логичность решения.
Основное внимание будет уделено правильному толкованию слов и фраз в условии задачи, выбору алгебраических операций для описания связей между неизвестными величинами и правильному выбору обозначений для переменных.
Кроме того, мы рассмотрим примеры, демонстрирующие различные ситуации и ошибки, которые можно допустить в процессе понимания условия задачи и обозначения переменных. Научившись четко формулировать условие задачи и обозначать неизвестные, вы сможете успешно приступить к их решению.
Использование уравнений для построения системы равнений
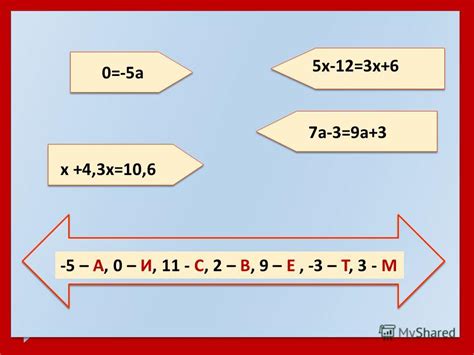
В данном разделе рассмотрим методы использования алгебраических уравнений для формирования системы уравнений. Такой подход позволяет находить решения задач, описывающих взаимосвязь нескольких величин или неизвестных.
Использование уравнений для составления системы уравнений является одним из важных инструментов в алгебре. Это позволяет свести сложные задачи к системе уравнений, которую можно решить последовательным анализом и вычислениями.
Основная задача при составлении системы уравнений - выразить каждую величину или неизвестную в зависимости от других и записать эти связи в виде уравнений. Для этого используются различные операции алгебры, такие как умножение, деление, сложение и вычитание.
Алгебраические уравнения могут описывать различные ситуации, такие как равенство, пропорциональность, зависимость и другие математические отношения. Используя эти уравнения, можно найти значения неизвестных, определить зависимости между величинами, провести анализ и решить задачу.
Построение системы уравнений требует аккуратной и точной работы, чтобы избежать ошибок и получить правильное решение. Основные шаги при составлении системы уравнений включают анализ условий задачи, перевод естественного языка в математическую форму, создание уравнений и последующее их решение.
Использование уравнений для составления систем уравнений позволяет эффективно решать задачи по алгебре, где требуется анализировать и взаимодействие нескольких величин. Этот подход позволяет построить математическую модель задачи, что упрощает ее решение и позволяет получить точный ответ.
Метод подстановки и объединение аналогичных членов

Этот раздел посвящен методу подстановки и объединению аналогичных членов, которые широко применяются при решении задач по алгебре в 9 классе. Метод подстановки представляет собой процесс замены переменных или выражений в алгебраическом выражении с целью получения уравнения, которое легче решить. Объединение аналогичных членов в свою очередь позволяет упростить алгебраическое выражение путем сложения или вычитания подобных слагаемых.
Использование метода подстановки является эффективным способом решения сложных задач, где необходимо упростить выражение или найти значение переменной. Сначала мы заменяем одну переменную на другую, чтобы получить новое уравнение, которое может быть решено более простыми методами. Затем мы подставляем значение найденной переменной в исходное уравнение, чтобы получить окончательный ответ.
Объединение аналогичных членов – это процесс сокращения алгебраического выражения путем сложения или вычитания слагаемых с одинаковыми переменными и степенями. Это позволяет нам упростить выражение и представить его в более компактной и понятной форме. При этом важно учитывать знак каждого слагаемого и правильно сгруппировать их.
- Определение метода подстановки и его роль в решении задач
- Примеры применения метода подстановки в алгебре 9 класса
- Определение и применение объединения аналогичных членов
- Практические примеры объединения аналогичных членов в алгебре 9 класса
- Сравнение эффективности метода подстановки и объединения аналогичных членов
Используя метод подстановки и объединение аналогичных членов, вы сможете более легко и точно решать задачи по алгебре, получая более простые и понятные выражения, а также находя значения переменных. Эти методы являются важными инструментами в изучении математики и подготовке к экзаменам.
Применение формул и свойств алгебры для упрощения выражений

Формулы и свойства алгебры - это набор математических правил и законов, которые позволяют нам переходить от сложных выражений к более простым и понятным. Использование этих формул и свойств позволяет нам сократить количество операций и упростить процесс решения задач.
К примеру, сочетание сложений и вычитаний в одно сложение (вычитание) может существенно сократить количество операций при раскрытии скобок и упростить выражение. Также, применение формулы для квадратного трехчлена позволяет нам упростить и решить выражение без необходимости выполнения длительных вычислений.
Рациональные выражения также могут быть упрощены с использованием формул и свойств алгебры. Мы можем сократить дроби и привести выражение к наиболее простому виду, что существенно облегчает решение задач.
В этом разделе мы изучим и разберем примеры применения различных формул и свойств алгебры для упрощения выражений, что поможет нам более эффективно решать задачи и улучшать наши навыки в алгебре.
Сокращение и раскрытие скобок для вычисления значений неизвестных
Этот раздел рассмотрит различные методы сокращения и раскрытия скобок в алгебраических выражениях, позволяющих получить значения неизвестных. Эти методы пригодятся при решении задач и упрощении сложных алгебраических выражений, что поможет найти конкретные значения переменных.
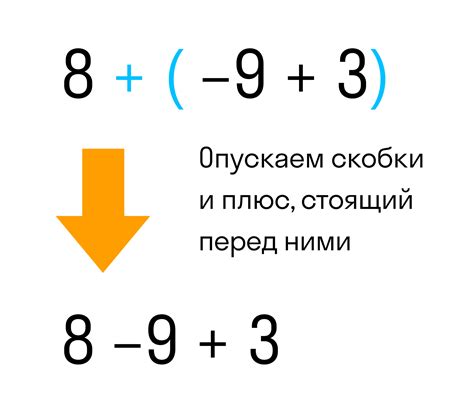
Сокращение скобок - это процесс упрощения выражения, удаляя скобки внутри него. Мы будем использовать различные методы, включая дистрибутивность умножения и правило сокращения скобок с одинаковыми знаками.
Раскрытие скобок - это процесс умножения каждого элемента внутри скобок на коэффициент снаружи скобок. Это позволяет получить новое алгебраическое выражение, которое может быть более простым для дальнейших вычислений.
Для более наглядного понимания процесса сокращения и раскрытия скобок, рассмотрим примеры и покажем шаги, необходимые для получения значений неизвестных.
| Пример | Процесс |
|---|---|
| 3(a + 2b) | Сокращение скобок: 3a + 6b |
| 2(x - 5) | Раскрытие скобок: 2x - 10 |
| (a - b)(c + d) | Раскрытие скобок: ac + ad - bc - bd |
Использование этих методов позволит упростить алгебраические выражения и получить значения неизвестных, что важно при решении задач и работе с алгеброй в 9 классе.
Проверка полученного решения и его толкование

В данном разделе осуществляется анализ и оценка решения алгебраической задачи, а также его интерпретация с целью подтверждения правильности и понимания полученных результатов.
В процессе проверки решения используются различные методы, такие как подстановка, эквивалентные преобразования, обратная проверка и интерпретация полученных числовых значений. Определение соответствия решения условиям задачи и удовлетворения всем требованиям является важным этапом, позволяющим удостовериться в корректности работы.
При интерпретации полученного решения необходимо детальное понимание математической модели, используемой в задаче, а также анализ результатов с учетом контекста и природы величин. Интерпретация позволяет расширить понимание задачи, выявить ее смысловую сущность и применимость в реальной жизни.
Использование метода визуализации для изучения проблемы
Применение графического метода для анализа задач дает возможность лучше понять условие задачи, определить ключевые элементы и связи между ними, а также проанализировать возможные варианты решения. При этом, использование графического метода помогает упростить задачу, разложить ее на более мелкие части и поэтапно подходить к решению.
Кроме того, графический метод позволяет наглядно представить различные значения и их взаимосвязь, что в свою очередь упрощает анализ и позволяет найти оптимальное решение. Также, благодаря использованию графического метода, можно обнаружить скрытые закономерности и регулярности, которые помогут лучше понять суть проблемы и найти наиболее эффективное решение.
Применение метода замены переменных для упрощения арифметических операций

В данном разделе рассмотрим эффективный метод применения замены переменных, который позволяет значительно упростить вычисления в алгебре. Применение этого метода позволяет сократить сложные числовые выражения и сделать их более понятными для решения задач.
Основная идея метода заключается в подстановке новой переменной вместо уже существующей, что помогает сократить выражение и облегчить решение задач. Новая переменная может быть выбрана таким образом, чтобы выполнять определенные требования, например, упростить дроби или сократить коэффициенты перед переменными.
- Преимущества метода:
- Упрощение сложных выражений
- Сокращение коэффициентов перед переменными
- Облегчение вычислений
- Понятность и логичность решений
- Шаги применения метода замены переменных:
- Анализ исходного выражения
- Определение новой переменной
- Подстановка новой переменной вместо старой
- Упрощение выражения с использованием новой переменной
- Решение упрощенного выражения
- Проверка полученного результата
- Пример применения метода замены переменных:
Допустим, у нас есть следующее выражение: 3x - 2x + 5y - 2y.
Заменим переменную x на a и переменную y на b. Теперь выражение будет выглядеть следующим образом: 3a - 2a + 5b - 2b.
Упростим полученное выражение: a + 3b.
Таким образом, применение метода замены переменных является эффективным способом упрощения арифметических операций в алгебре, что упрощает решение задач и позволяет получить более понятный результат.
Разложение выражений на множители для достижения корней

Процесс разложения выражения на множители основывается на том факте, что любое многочленное выражение может быть представлено в виде произведения нескольких множителей. При разложении мы ищем такие множители, которые при умножении вместе дают исходное выражение.
Разложение на множители позволяет найти корни алгебраического выражения. Корень – это значение переменной, для которого исходное выражение равно нулю. Определение корней имеет важное значение при решении уравнений и нахождении значений переменных.
В данном разделе мы рассмотрим различные методы разложения выражений на множители, такие как: разложение на множители с общими множителями, разложение на множители по степеням, разложение на множители при помощи биномиальной формулы, разложение на множители с использованием правила двух квадратов и другие. Каждый из этих методов имеет свои особенности и применяется в различных ситуациях.
Применение разложения выражений на множители для нахождения корней позволяет упростить алгебраические выражения, а также обобщить их свойства. Благодаря этому методу мы можем проводить расчеты и анализировать уравнения с высокой точностью и эффективностью.
Использование разнообразных методов для разрешения задач: аналитические и геометрические подходы

Аналитический подход основан на алгебре и математическом анализе. Он заключается в использовании формул, уравнений и свойств математических объектов для анализа и выявления закономерностей. Аналитический подход позволяет нам провести вычисления, найти значения переменных или функций и найти решения для уравнений или систем уравнений.
Геометрический подход, в свою очередь, основан на применении геометрических свойств и отношений. Здесь мы используем достоинства геометрических фигур, теоремы и правила для анализа задачи. Геометрический подход может представляться в виде построения графиков, использования координат и отношений между точками и фигурами.
В зависимости от задачи и ее условий, определенный подход может оказаться более предпочтительным или эффективным. Некоторые задачи легче решать аналитическими методами, когда другие могут требовать геометрического подхода. Комбинирование разных методов позволяет нам получить более полное и точное решение задачи.
Вопрос-ответ

Какой способ решения задачи по алгебре 9 класс номер 479 можно использовать?
В задаче номер 479 можно использовать метод подстановки или метод проб и ошибок для поиска и нахождения корня уравнения.
Можно ли для решения задачи номер 479 использовать графический метод?
Нет, графический метод не является подходящим способом для решения задачи номер 479. В данной задаче требуется найти численное значение корня уравнения.