Математическая индукция представляет собой процесс построения цепочки доказательств для каждого натурального числа, начиная с базового случая и применяя некоторое индуктивное предположение. Такой подход позволяет обобщить результаты для всего множества натуральных чисел.
Для доказательства деления выражения на число с помощью метода математической индукции необходимо сформулировать базовый случай для наше вводного утверждения и показать его истинность. Затем проводится шаг индукции, в котором доказывается, что если утверждение верно для некоторого натурального числа, то оно верно и для следующего числа. Таким образом, утверждение приобретает общую истинность.
Основные принципы и применение метода математической индукции

Основные принципы метода математической индукции сводятся к следующим этапам:
| Шаг 1: | Базовый шаг. Доказывается верность утверждения для некоторого начального значения или набора значений. Этот шаг позволяет убедиться, что утверждение верно для хотя бы одного значения. |
| Шаг 2: | Шаг индукции. Предполагается, что утверждение выполнено для некоторого значения (или для набора значений), и доказывается, что оно выполнено и для следующего значения (или для любого значения, следующего за предыдущим). Таким образом, это позволяет установить его выполнение для всех последующих значений. |
| Шаг 3: | Получение общего утверждения. Как результат повторения шага индукции для всех возможных значений, утверждение считается доказанным для всех натуральных чисел или множества объектов. |
Основные принципы и принципы функционирования метода математической индукции
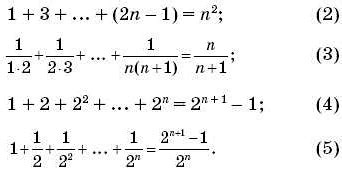
Основная идея метода состоит в разбиении рассматриваемого утверждения на два шага: базовый шаг и шаг индукции. В базовом шаге доказывается верность утверждения для начального значения, обычно это натуральное число 1. Затем, в шаге индукции, предполагаем, что утверждение выполняется для некоторого числа k и доказываем его верность для числа k+1.
Суть шага индукции заключается в том, что предположение о верности утверждения для числа k позволяет доказать его верность для числа k+1. Этот процесс продолжается для всех натуральных чисел, что гарантирует верность утверждения для всех чисел больше (или равных) базового значения.
Использование метода математической индукции помогает математикам обосновать и доказать верность сложных утверждений, а также разрабатывать новые теории и алгоритмы на основе уже установленных и закономерностей.
Использование математической индукции для подтверждения деления выражения на число

В данном разделе будет представлено доказательство деления выражения на число с использованием мощного метода математической индукции.
Математическая индукция - это метод доказательства утверждений, использующий два шага: базовый и индукционный. Он основан на предположении, что если утверждение верно для некого значения (базового случая), а также при условии, что оно верно для следующего значения (индукционный случай), то оно будет верно для всех последующих значений.
В нашем случае мы рассматриваем деление выражения на число. Мы предполагаем, что данное выражение делится на это число и хотим доказать, что это утверждение верно для всех возможных значений выражения.
Мы начинаем с базового случая, выбирая некое начальное значение выражения. Затем мы проводим индукционный шаг, предполагая, что если утверждение верно для некого значения, то оно также верно для следующего значения. После этого мы доказываем, что утверждение действительно верно для следующего значения путем применения алгоритма деления и арифметических операций.
Таким образом, мы устанавливаем, что выражение делится на число. Доказательство с использованием математической индукции позволяет нам убедиться в корректности деления и расширить его применимость на различные значения выражения, что является важным инструментом в математике и науке.
Начальный шаг доказательства: базовый случай и его особенности

В самом начале математической индукции, когда мы стремимся доказать утверждение для всех натуральных чисел, необходимо провести начальный шаг доказательства. Этот шаг играет важную роль, поскольку он покрывает базовый случай, от которого начинается цепочка рассуждений для всех остальных чисел. В этом разделе мы рассмотрим особенности базового случая и как его анализировать.
Базовый случай может иметь уникальные особенности, которые специфичны для конкретной задачи или переменной, с которой мы работаем. Важно уделить особое внимание этим особенностям, поскольку они могут влиять на наше доказательство и наше понимание проблемы. Ключевыми характеристиками, которые мы будем рассматривать, являются исключительные значения, ограничения на переменные и строка рассуждений, которая приводит к базовому случаю.
Анализ базового случая позволяет нам убедиться, что утверждение верно хотя бы для одного элемента или значения, и тем самым является стартовой точкой для доказательства утверждения для всей последовательности. Поэтому важно внимательно проанализировать базовый случай и убедиться, что он корректно подтверждает наше утверждение.
| Важно знать: | Базовый случай является фундаментом для доказательства методом математической индукции и его корректность является неотъемлемой частью успешного доказательства. |
Шаг индукции: предположение и анализ

Предположение
Перед тем, как начать доказательство, мы должны сделать предположение о верности утверждения для некоторого фиксированного значения. В нашем случае, мы предполагаем, что деление выражения на число выполняется правильно для некоторого числа n. Другими словами, мы предполагаем, что утверждение верно для n.
Анализ
После того, как мы сделали предположение, мы переходим к анализу. В анализе мы рассматриваем выражение и применяем математические операции и свойства, чтобы вывести новое утверждение. Мы стараемся применять индукцию и использовать предположение, чтобы доказать утверждение для числа n+1.
Анализ чаще всего включает в себя использование арифметических правил, законов ассоциативности и коммутативности, свойств операций и других математических инструментов для преобразования выражения и получения новой формы, которая доказывает справедливость утверждения для (n+1).
Заключение
Шаг индукции - это важный компонент математической индукции, который позволяет нам доказывать утверждение для всех чисел, используя предположение и анализ. Деление выражения на число - один из примеров, где метод индукции может быть успешно применен для подтверждения верности утверждения во всем диапазоне чисел.
Как сформулировать верное предположение при применении принципа математической индукции?

Предположение должно быть конкретным и точным, чтобы обеспечить строгую логику доказательства. В нем могут использоваться синонимы и разнообразные выражения, чтобы избежать повторения одних и тех же слов.
Важно отметить, что предположение должно быть основано на индуктивном переходе – связи между соседними членами последовательности. Оно должно вытекать из уже доказанных базовых утверждений и представлять собой следующую логическую ступень. Это позволит обеспечить прогрессию от одного значения к другому и доказать истинность для всех чисел.
Корректное выражение предположения – важный шаг в доказательстве методом математической индукции. Оно должно быть ясным, точным и строго связано с уже установленными утверждениями, чтобы обеспечить верное и законченное доказательство.
Осмотр шага индукции: способы доказательства деления арифметического выражения на конкретное значение

Когда мы проводим доказательство методом математической индукции, важно аккуратно анализировать каждый шаг этого процесса. В данном разделе мы рассмотрим различные способы доказательства деления заданного арифметического выражения на конкретное значение, подчеркивая значимость правильного выбора стратегии для успешного завершения доказательства.
В процессе доказательства мы используем различные методы и приемы, чтобы убедиться в корректности деления выражения на число. Можем обращать особое внимание на факторизацию выражения или использовать подход, основанный на свойствах арифметических операций. Также можно применять подстановку, замену переменных или преобразование выражений для достижения нужного результата.
Важно понимать, что выбор метода зависит от конкретных характеристик выражения и требуемого результата. Иногда мы можем применить прямой метод, продемонстрировав, что при делении на число выражение равно нулю или другому конкретному значению. В других случаях мы можем использовать принцип доказательства от противного, предполагая, что деление невозможно, и приходя к противоречию.
Итак, в этом разделе мы рассмотрели различные стратегии и подходы к доказательству деления арифметического выражения на конкретное число. Помните, что правильный выбор метода и аккуратное проведение каждого шага индукции играют решающую роль в достижении успешных результатов в математическом анализе.
Вопрос-ответ

Зачем нужно делить выражение на число с использованием метода математической индукции?
Метод математической индукции позволяет доказать утверждения о целочисленных выражениях, включая деление. Он основывается на принципе математической индукции, который позволяет установить истинность утверждения для всех натуральных чисел.
Каким образом применяется метод математической индукции для деления выражения на число?
Для доказательства деления выражения на число с использованием метода математической индукции, необходимо сначала показать, что утверждение верно для наименьшего значениия, а затем показать, что оно верно для следующего значения, предполагая, что оно верно для предыдущего. Проводя такие доказательства последовательно для всех натуральных чисел, можно установить истинность утверждения для любых значений.
Можно ли применять метод математической индукции для деления выражений с дробными числами?
Метод математической индукции применяется для доказательства утверждений о целочисленных выражениях, поэтому он не применяется для деления выражений с дробными числами. Для доказательства таких утверждений используются другие методы и свойства дробных чисел.
Какая формула используется при делении выражения на число с использованием метода математической индукции?
При делении выражения на число с использованием метода математической индукции используется формула: (P(0) && (P(k) -> P(k+1))) -> (forall n (P(n))), где P(n) - утверждение оценивающееся для каждого значения n.
Какая роль математической индукции в делении выражений на число?
Метод математической индукции играет важную роль в делении выражений на число, позволяя доказать истинность утверждений для всех натуральных чисел. Применяя этот метод, можно установить истинность деления выражений на число в общем случае, а не только для отдельных примеров.



