В современном мире невозможно представить свою жизнь без систем, которые помогают нам измерять и анализировать величины и изменения вокруг нас. Все начинается со способа, которым мы измеряем. Если вспомнить школьные уроки физики и математики, то мы точно помним обычную систему отсчета, которую привыкли использовать с самого детства. Но существует и другая, альтернативная система, которая становится все более популярной и находит свое применение в различных областях науки и технологий.
Главное отличие этой альтернативной системы отсчета от традиционной заключается в использовании необычных элементов и принципов. Они позволяют измерять и описывать явления, которые не всегда укладываются в рамки привычных величин и единиц измерения. Благодаря этим элементам и принципам, мы можем более точно и полно описывать и понимать мир вокруг нас.
Одним из ключевых элементов этой системы является использование синонимов и аналогий. Каждый элемент имеет свой синоним, который помогает нам найти аналогию с уже известной и понятной нам величиной или явлением. Таким образом, мы можем увидеть и сравнить объекты или явления, которые кажутся несравнимыми или слишком сложными для измерения с помощью обычной системы отсчета.
Структура и состав основных компонентов системы измерения 2-го варианта учебной программы для 9 класса

Когда мы говорим о системе измерения 2-го варианта, мы подразумеваем присутствие определенных элементов и основных компонентов, необходимых для ее функционирования. В этом разделе рассмотрим структуру и состав этих основных компонентов, которые позволяют нам проводить измерения и оценивать различные величины и параметры.
Первым важным компонентом системы является система единиц измерения. Это набор стандартных значений, которые мы используем для измерения определенных величин. Система единиц определяет масштаб и отношение между измеряемыми значениями и позволяет нам сравнивать и оценивать их. Каждая единица измерения имеет свое название и символ, которые позволяют нам однозначно указывать на то, какую величину мы хотим измерить.
Вторым важным компонентом системы являются измерительные инструменты. Они представляют собой физические устройства, с помощью которых мы производим измерения. Измерительные инструменты могут быть различного типа в зависимости от величины, которую мы хотим измерить. Они могут быть механическими, электронными или оптическими, и каждый тип инструмента имеет свои особенности и принцип работы.
Третий компонент системы - это методы измерения. Они определяют способы и правила, которые мы используем для выполнения измерений. Методы измерения включают в себя различные алгоритмы и процедуры, которые позволяют нам надежно и точно определить значения величин. Методы измерения могут быть стандартизированными и регламентированными, чтобы обеспечить единообразие и согласованность результатов измерений.
- Система единиц измерения
- Измерительные инструменты
- Методы измерения
- Система обработки и анализа данных
Числовая последовательность
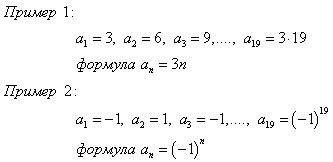
Числовая последовательность представляет собой упорядоченный набор чисел, где каждое следующее число зависит от предыдущего. Это позволяет нам визуализировать структуру и установить связь между элементами последовательности. Важно отметить, что числовые последовательности могут быть как монотонными (возрастающими или убывающими), так и иметь различные закономерности изменения элементов.
| Обозначение | Описание |
|---|---|
| an | Общий член последовательности, где n - номер элемента |
| a1 | Первый элемент последовательности |
| an - an-1 | Разность между двумя последовательными элементами |
| Sn | Сумма первых n-элементов последовательности |
Числовые последовательности могут применяться в различных научных и практических областях, таких как физика, экономика, информатика и другие. Они являются неотъемлемой частью изучения и анализа широкого спектра явлений и процессов.
Познакомившись с основными понятиями и принципами числовых последовательностей, мы сможем получить новые инструменты для анализа и построения моделей, а также расширить наше понимание мира, основанного на числах и их характеристиках.
Разряды числа: какое значение они несут и почему они важны
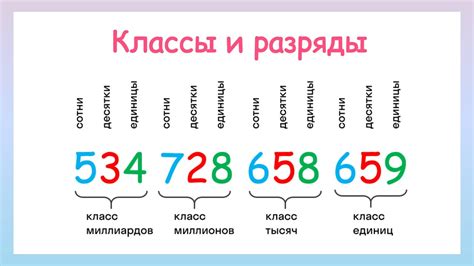
Когда мы работаем с числами, мы обычно представляем их в виде цифр. Но помимо самих цифр, каждое число имеет свои особенности и характеристики, которые помогают нам понять его значение и положение в числовой системе. Эти характеристики называются разрядами числа.
Разряды числа выполняют важную роль в математике и ее применениях, таких как физика, экономика, программирование и т. д. Они не только помогают нам переводить числа из одной системы счисления в другую, но и позволяют нам работать с числами различной величины и точности.
- Разряд единиц: этот разряд указывает на количество единиц в числе, например, в числе 123 разряд единиц равен 3.
- Разряд десятков: этот разряд указывает на количество десятков в числе, например, в числе 123 разряд десятков равен 2.
- Разряд сотен: этот разряд указывает на количество сотен в числе, например, в числе 123 разряд сотен равен 1.
Кроме того, существуют и другие разряды, такие как тысячи, десятки тысяч, сотни тысяч и т. д., которые помогают нам работать с большими числами. Каждый разряд имеет свое значение и позволяет нам точно определить порядок числа и его значимость в контексте задачи.
Теперь, когда мы понимаем, какие разряды числа существуют и какое значение они несут, мы можем более точно и эффективно работать с числами и использовать их в различных математических операциях и задачах.
Системы счисления: отражение многообразия чисел в разнообразии символов

Системы счисления включают в себя множество основных элементов, среди которых числа, основание системы, разряды и разнообразные правила и операции. Каждый элемент системы счисления играет свою уникальную роль и определяет способ представления и выполнения математических операций над числами.
- Числа в системе счисления определяют допустимые символы, которые могут использоваться в записи числовых значений. Это могут быть цифры от 0 до 9, буквы алфавита или иные символы, которые выбираются в соответствии с выбранной системой.
- Основание системы счисления определяет, сколько различных символов может использоваться для представления чисел. Например, в десятичной системе счисления основание равно 10, так как доступны цифры от 0 до 9.
- Разряды в системе счисления определяют позиционное значение каждого символа в числе. Слева направо, значения разрядов увеличиваются в геометрической прогрессии.
Правила и операции, применяемые в системе счисления, определяют, каким образом выполняются основные математические операции, такие как сложение, вычитание, умножение и деление. Различные системы счисления могут предоставлять уникальные методы для выполнения этих операций, а также дополнительные операции, специфичные для данной системы.
Основа системы счисления: строительные блоки и базовые принципы

Основание системы счисления - это концептуальная основа, которая поддерживает все числовые операции и участие символов в числовых комбинациях. Оно определяет количество доступных символов, а также их значения и порядок. Для каждого основания системы счисления существует определенное количество символов, которые используются для представления чисел. Например, основание 10, которое является наиболее распространенным в нашей повседневной жизни, имеет 10 символов: от 0 до 9.
Основание системы счисления имеет еще один важный аспект - порядок символов. Это связано с позиционной системой счисления, которая определяет, как каждый символ конкретного числа влияет на его общую стоимость. Например, в десятичной системе цифра 5, находящаяся в числе 546, имеет различные значения в зависимости от ее позиции (единицы, десятки, сотни). Порядок символов ставит каждую позицию в определенное место относительно других, чтобы выразить правильное значение и общую стоимость числа.
Таким образом, основание системы счисления играет роль конструктивного элемента, определяющего количество доступных символов и их порядок использования. От понимания и усвоения основания зависит корректность и точность числовых представлений и операций внутри данной системы счисления.
Преобразование чисел из одной системы счисления в другую

Обозначим, как произвольное число в исходной системе счисления N, которое нужно перевести в новую систему счисления M. Для этого сначала необходимо разложить число N на сумму степеней основы исходной системы счисления. Затем, используя таблицу соответствия, осуществить перевод числа в новую систему счисления M. Этот процесс требует внимательного анализа информации и правильного выбора соответствующих знаков и цифр для новой системы счисления.
Примером преобразования числа может быть перевод числа 101 из двоичной системы счисления в десятичную систему счисления. Для этого раскладываем число по степеням двойки: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 5. Таким образом, число 101 в двоичной системе счисления эквивалентно числу 5 в десятичной системе счисления.
В зависимости от конкретной задачи и системы счисления, преобразование чисел может включать в себя дополнительные шаги или более сложные алгоритмы. Однако, основные принципы остаются неизменными - разложение числа по степеням основы исходной системы счисления, а затем перевод числа в новую систему счисления с использованием таблицы соответствия.
Практическое применение системы счисления второго варианта для учеников девятого класса: примеры и задачи

В данном разделе мы рассмотрим практическое использование системы счисления второго варианта для учеников девятого класса. Мы представим примеры и задачи, которые помогут вам лучше понять и отработать основные принципы этой системы.
Одним из примеров практического применения системы счисления второго варианта является использование ее в информатике и программировании. В этих областях знание этой системы отсчета необходимо для работы с битами, байтами и другими цифровыми данными. Например, при работе с цифровыми изображениями мы используем эту систему для представления цветовых значений пикселей.
Кроме того, система счисления второго варианта может применяться в математике для решения задач связанных с двоичными числами. Например, при решении задач о перемножении и делении двоичных чисел, мы используем основные элементы этой системы – нули и единицы, а также правила сложения и умножения чисел.
Необходимость понимания системы счисления второго варианта также возникает в электронике и схемотехнике. При разработке и проектировании цифровых устройств, например, компьютеров или микроконтроллеров, это знание является основополагающим. Оно позволяет понимать принципы работы сигналов, логических операций и кодирования информации.
| Примеры практического применения системы счисления второго варианта: |
|---|
| • Кодирование информации в компьютерах и информационных системах |
| • Работа с битовыми операциями в программировании |
| • Решение задач по двоичной арифметике и логике |
| • Построение схем и проектирование электронных устройств |
Вопрос-ответ

Какие основные элементы входят в систему отсчета 2 вариант для 9 класса?
Основными элементами системы отсчета 2 вариант для 9 класса являются цифры 0-1 и значение каждой цифры в разряде, а также его позиция в числе.
Какие принципы лежат в основе системы отсчета 2 вариант для 9 класса?
Основными принципами системы отсчета 2 вариант для 9 класса являются позиционный принцип и двоичный принцип. Позиционный принцип заключается в том, что значение каждой цифры в числе зависит от ее позиции в записи числа. Двоичный принцип означает, что система отсчета использует только две цифры - 0 и 1.
Как использовать систему отсчета 2 вариант для решения математических задач в 9 классе?
Система отсчета 2 вариант может быть использована для решения различных математических задач в 9 классе. Например, она может быть использована для работы с двоичными числами, битами и байтами в информатике, а также для решения задач по счету и переводу чисел.
Какие преимущества имеет система отсчета 2 вариант для 9 класса по сравнению с десятичной системой отсчета?
Одним из преимуществ системы отсчета 2 вариант для 9 класса является компактность и удобство представления чисел. Также она имеет простую структуру и широко применяется в информационных технологиях. Кроме того, система отсчета 2 вариант позволяет более эффективно работать с двоичными данными и легко выполнять операции сложения и умножения.
Как может быть использована система отсчета 2 вариант для 9 класса в реальной жизни?
Система отсчета 2 вариант для 9 класса широко применяется в информационных технологиях, например, в компьютерах и сетях. Она используется для представления, обработки и передачи данных. Также она может быть применена в задачах связанных с кодированием, шифрованием и компьютерной графикой.
Какие основные элементы входят в систему отсчета 2 вариант для 9 класса?
Система отсчета 2 вариант для 9 класса включает в себя следующие основные элементы: числа, цифры, знаки операций (плюс, минус, умножение, деление), арифметические действия, приоритеты операций, скобки для задания порядка выполнения действий.



