В мире геометрии существуют некоторые закономерности и свойства, которые поражают своей красотой и простотой. Одно из таких свойств - это способность биссектрис вертикальных углов доказывать развернутый угол. Это удивительное открытие открывает перед нами новые возможности для изучения и применения геометрических фигур и физических явлений, где углы играют главную роль.
Биссектрисы, по своей сути, являются разделителями углов на две равные части. Они призваны раскрывать перед нами симметрию и равенство, помогая нам понять природу форм и пространственных осей. Вертикальные углы, в свою очередь, как будто соединяют землю с небесами, устанавливая границы и пропорции между горизонтальными и вертикальными плоскостями.
Основные понятия и определения

В данном разделе рассмотрим основные понятия и определения, связанные с углами, которые характеризуются биссектрисами и вертикальными взаимодействиями. С помощью углов мы можем определить направления и расположение объектов, а также анализировать их свойства и взаимодействия.
- Угол: это геометрическая фигура, образованная двумя полупрямыми с общим началом, называемым вершиной. Углы широко используются в геометрии и физике.
- Биссектриса: это линия или отрезок, который делит угол на две равные части. Она проходит через вершину угла и делит его на две равные "половины".
- Вертикальные углы: это пары углов, расположенных друг напротив друга на пересекающихся прямых линиях. Вертикальные углы равны друг другу и имеют одинаковую величину.
Используя данные определения, мы можем лучше понять структуру и свойства углов, а также их взаимосвязи с другими углами. Биссектрисы и вертикальные углы играют важную роль в решении геометрических задач и доказательств, позволяя нам анализировать и описывать различные угловые отношения и свойства.
Определение взаимной величины внутренних углов при пересечении
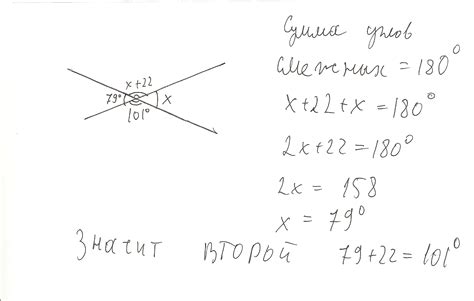
Взаимная величина внутренних углов - это показатель угла, образованного двумя пересекающимися прямыми, который значительно влияет на форму и взаимное расположение этих прямых. Чтобы правильно определить величину угла при пересечении, необходимо учесть различные факторы, такие как их ориентация и направление.
Определение взаимной величины внутренних углов имеет свои особенности и требует точного измерения. Важно обратить внимание на прилегающие углы, а также углы, которые образуются при пересечении двух прямых. Значение этой величины может быть положительным или отрицательным, в зависимости от направления обеих прямых. Величина угла также может быть развернутой, что указывает на его относительное направление относительно других углов.
Определение оси симметрии вертикальных углов
В предыдущих разделах мы рассматривали углы и их свойства. В данном разделе мы сосредоточимся на особой линии, называемой "осью симметрии". Эта линия играет важную роль в определении вертикальных углов и позволяет нам установить равенство между ними.
Ось симметрии вертикальных углов - это линия, которая делит угол пополам и является его симметричной осью. Она проходит через вершину угла и делит его на две равные части, подобно зеркалу.
Для определения оси симметрии вертикальных углов мы можем использовать графический метод или использовать аналитическую геометрию. Графический метод включает построение геометрических фигур, таких как треугольники и окружности, для определения оси симметрии. Аналитическая геометрия использует систему координат и математические выражения для определения координат оси симметрии.
Таблица 1: Методы определения оси симметрии вертикальных углов
| Метод | Описание |
|---|---|
| Графический метод | Использует построение геометрических фигур для определения оси симметрии |
| Аналитическая геометрия | Использует систему координат и математические выражения для определения оси симметрии |
Ось симметрии вертикальных углов играет важную роль при доказательстве равенства этих углов. Зная, что ось симметрии делит угол пополам, мы можем использовать это свойство для доказательства, что два вертикальных угла равны между собой.
Свойства линий, которые делят углы пополам и имеют общее начало

Биссектрисы являются важным инструментом для решения геометрических задач, а также имеют несколько свойств, которые можно использовать для доказательства различных утверждений. Одно из таких свойств связано с вертикальными углами. Вертикальные углы образуются при пересечении двух прямых линий и имеют равные меры. Доказательство развернутого угла рассматривает биссектрисы этих вертикальных углов и их важную роль в получении равенства мер двух углов.
Изучение свойств биссектрис вертикальных углов позволяет нам развивать наши навыки в решении геометрических задач и лучше понимать структуру углов в пространстве. В данном разделе мы подробно рассмотрим эти свойства, исследуем их особенности и применение в различных ситуациях. При этом мы будем использовать другие термины и выражения, чтобы представить информацию более разнообразно и интересно.
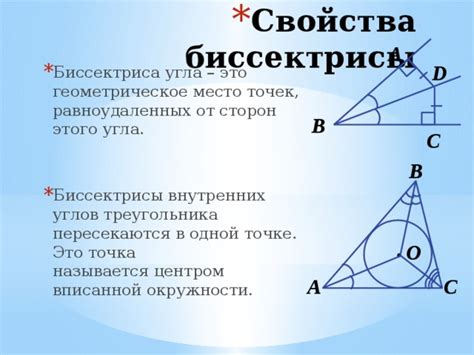
Идея доказательства развернутого угла с использованием биссектрис вертикальных углов
Вопрос-ответ

Зачем нужно доказательство развернутого угла?
Доказательство развернутого угла позволяет убедиться в том, что сумма двух вертикальных углов всегда равна 180 градусов. Это понимание является важным и базовым элементом геометрии, который используется во многих задачах и теоремах.
Что такое биссектрисы вертикальных углов?
Биссектрисы вертикальных углов - это прямые линии, которые делят вертикальные углы пополам. Они проходят через точку пересечения вертикальных углов и располагаются по обеим сторонам пересекающей прямой.
Каким образом биссектрисы вертикальных углов помогают доказать развернутый угол?
Биссектрисы вертикальных углов помогают доказать развернутый угол с помощью применения геометрических теорем и свойств. Одной из таких теорем является теорема о сумме углов треугольника. Когда биссектрисы вертикальных углов пересекаются, они образуют треугольники, в которых сумма углов равна 180 градусов. Это позволяет сделать вывод о том, что сумма вертикальных углов также равна 180 градусов.
Можно ли использовать биссектрисы вертикальных углов в других задачах, кроме доказательства развернутого угла?
Да, биссектрисы вертикальных углов могут быть использованы и в других задачах геометрии. Например, они помогают находить углы, секущие и касательные, отражения и гомотетии, а также определять границы множеств в пространстве. Биссектрисы вертикальных углов являются важным инструментом для решения геометрических задач и проведения геометрических доказательств.



